از ویکیپدیا، دانشنامهٔ آزاد
توزیع گمپرتز
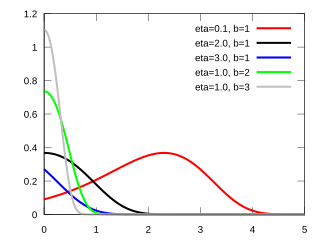
تابع چگالی احتمال
تابع توزیع تجمعی
پارامترها
η
,
b
>
0
{\displaystyle \eta ,b>0\,\!}
تکیهگاه
x
∈
[
0
,
∞
)
{\displaystyle x\in [0,\infty )\!}
تابع چگالی احتمال
b
η
e
b
x
e
η
exp
(
−
η
e
b
x
)
{\displaystyle b\eta e^{bx}e^{\eta }\exp \left(-\eta e^{bx}\right)}
تابع توزیع تجمعی
1
−
exp
(
−
η
(
e
b
x
−
1
)
)
{\displaystyle 1-\exp \left(-\eta \left(e^{bx}-1\right)\right)}
میانگین
(
1
/
b
)
e
η
Ei
(
−
η
)
{\displaystyle (1/b)e^{\eta }{\text{Ei}}\left(-\eta \right)}
where Ei
(
z
)
=
∫
−
z
∞
(
e
−
v
/
v
)
d
v
{\displaystyle {\text{where Ei}}\left(z\right)=\int \limits _{-z}^{\infty }\left(e^{-v}/v\right)dv}
میانه
(
1
/
b
)
ln
[
(
−
1
/
η
)
ln
(
1
/
2
)
+
1
]
{\displaystyle \left(1/b\right)\ln \left[\left(-1/\eta \right)\ln \left(1/2\right)+1\right]}
مُد
=
(
1
/
b
)
ln
(
1
/
η
)
{\displaystyle =\left(1/b\right)\ln \left(1/\eta \right)\ }
with
0
<
F
(
x
∗
)
<
1
−
e
−
1
=
0.632121
,
0
<
η
<
1
{\displaystyle {\text{with }}0<{\text{F}}\left(x^{*}\right)<1-e^{-1}=0.632121,0<\eta <1}
=
0
,
η
≥
1
{\displaystyle =0,\quad \eta \geq 1}
واریانس
(
1
/
b
)
2
e
η
{
−
2
η
3
F
3
(
1
,
1
,
1
;
2
,
2
,
2
;
−
η
)
+
γ
2
{\displaystyle \left(1/b\right)^{2}e^{\eta }\{-2\eta {\ }_{3}{\text{F}}_{3}\left(1,1,1;2,2,2;-\eta \right)+\gamma ^{2}}
+
(
π
2
/
6
)
+
2
γ
ln
(
η
)
+
[
ln
(
η
)
]
2
−
e
η
[
Ei
(
−
η
)
]
2
}
{\displaystyle +\left(\pi ^{2}/6\right)+2\gamma \ln \left(\eta \right)+[\ln \left(\eta \right)]^{2}-e^{\eta }[{\text{Ei}}\left(-\eta \right)]^{2}\}}
where
γ
is the Euler constant:
γ
=
−
ψ
(
1
)
=
0.577215...
{\displaystyle {\begin{aligned}{\text{ where }}&\gamma {\text{ is the Euler constant: }}\,\!\\&\gamma =-\psi \left(1\right)={\text{0.577215... }}\end{aligned}}}
and
3
F
3
(
1
,
1
,
1
;
2
,
2
,
2
;
−
z
)
=
∑
k
=
0
∞
[
1
/
(
k
+
1
)
3
]
(
−
1
)
k
(
z
k
/
k
!
)
{\displaystyle {\begin{aligned}{\text{ and }}{}_{3}{\text{F}}_{3}&\left(1,1,1;2,2,2;-z\right)=\\&\sum _{k=0}^{\infty }\left[1/\left(k+1\right)^{3}\right]\left(-1\right)^{k}\left(z^{k}/k!\right)\end{aligned}}}
تابع مولد گشتاور
E
(
e
−
t
x
)
=
η
e
η
E
t
/
b
(
η
)
{\displaystyle {\text{E}}\left(e^{-tx}\right)=\eta e^{\eta }{\text{E}}_{t/b}\left(\eta \right)}
with E
t
/
b
(
η
)
=
∫
1
∞
e
−
η
v
v
−
t
/
b
d
v
,
t
>
0
{\displaystyle {\text{with E}}_{t/b}\left(\eta \right)=\int _{1}^{\infty }e^{-\eta v}v^{-t/b}dv,\ t>0}
در علم احتمالات و آمار ، توزیع گمپرتز (Gompertz distribution ) یک توزیع احتمال پیوسته است که به بزرگداشت بنجامین گمپرتز (۱۸۶۵–۱۷۷۹) چنین نامگذاری شدهاست. این توزیع برای توصیفِ توزیع بازهٔ زندگی بزرگسالان با کمک جمعیتشناسی [ ۱] [ ۲] مرگر [ ۳] [ ۴] زیستشناسی [ ۵] پیریشناسی [ ۶] علوم رایانه برای مدلسازی نرخ شکست کدهای رایانه ای از توزیع گمپرتز استفاده میشود.[ ۷] ارزش طول عمر مشتری کاربرد دارد.[ ۸]
توزیع گمپرتز، یک توزیع انعطافپذیر است و ممکن است به راست یا چپ متمایل شود، تابع شکست آن یک تابع محدب
F
(
x
;
η
,
b
)
{\displaystyle F\left(x;\eta ,b\right)}
تابع چگالی گمپرتز بسته به مقدارهای مختلف پارامتر شکلی
η
{\displaystyle \eta \,\!}
هرگاه
η
≥
1
,
{\displaystyle \eta \geq 1,\,}
مُد تابع چگالی احتمالاتی در صفر خواهد بود.
هرگاه
0
<
η
<
1
,
{\displaystyle 0<\eta <1,\,}
x
∗
=
(
1
/
b
)
ln
(
1
/
η
)
with
0
<
F
(
x
∗
)
<
1
−
e
−
1
=
0.632121
{\displaystyle x^{*}=\left(1/b\right)\ln \left(1/\eta \right){\text{with }}0<F\left(x^{*}\right)<1-e^{-1}=0.632121}
هرگاه
f
1
{\displaystyle f_{1}}
f
2
{\displaystyle f_{2}}
واگرایی کولبک-لیبلر به صورت زیر خواهد بود:
D
K
L
(
f
1
∥
f
2
)
=
∫
0
∞
f
1
(
x
;
b
1
,
η
1
)
ln
f
1
(
x
;
b
1
,
η
1
)
f
2
(
x
;
b
2
,
η
2
)
d
x
=
ln
e
η
1
b
1
η
1
e
η
2
b
2
η
2
+
e
η
1
[
(
b
2
b
1
−
1
)
Ei
(
−
η
1
)
+
η
2
η
1
b
2
b
1
Γ
(
b
2
b
1
+
1
,
η
1
)
]
−
(
η
1
+
1
)
{\displaystyle {\begin{aligned}D_{KL}(f_{1}\parallel f_{2})&=\int _{0}^{\infty }f_{1}(x;b_{1},\eta _{1})\,\ln {\frac {f_{1}(x;b_{1},\eta _{1})}{f_{2}(x;b_{2},\eta _{2})}}dx\\&=\ln {\frac {e^{\eta _{1}}\,b_{1}\,\eta _{1}}{e^{\eta _{2}}\,b_{2}\,\eta _{2}}}+e^{\eta _{1}}\left[\left({\frac {b_{2}}{b_{1}}}-1\right)\,\operatorname {Ei} (-\eta _{1})+{\frac {\eta _{2}}{\eta _{1}^{\frac {b_{2}}{b_{1}}}}}\,\Gamma \left({\frac {b_{2}}{b_{1}}}+1,\eta _{1}\right)\right]-(\eta _{1}+1)\end{aligned}}}
در رابطهٔ بالا،
Γ
(
⋅
,
⋅
)
{\displaystyle \Gamma (\cdot ,\cdot )}
تابع گامای ناکامل بالایی و
Ei
(
⋅
)
{\displaystyle \operatorname {Ei} (\cdot )}
انتگرال نمایی است.[ ۹]
↑ Vaupel, James W. (1986). "How change in age-specific mortality affects life expectancy". Population Studies . 40 (1): 147–157. doi :10.1080/0032472031000141896 . ↑ Preston, Samuel H.; Heuveline, Patrick; Guillot, Michel (2001). Demography:measuring and modeling population processes . Oxford: Blackwell. ↑ Benjamin, Bernard; Haycocks, H.W.; Pollard, J. (1980). The Analysis of Mortality and Other Actuarial Statistics ↑ Willemse, W. J.; Koppelaar, H. (2000). "Knowledge elicitation of Gompertz' law of mortality". Scandinavian Actuarial Journal (2): 168–179. ↑ Economos, A. (1982). "Rate of aging, rate of dying and the mechanism of mortality". Archives of Gerontology and Geriatrics . 1 (1): 46–51. ↑ Brown, K.; Forbes, W. (1974). "A mathematical model of aging processes" . Journal of Gerontology . 29 (1): 46–51. doi :10.1093/geronj/29.1.46 . ↑ Ohishi, K.; Okamura, H.; Dohi, T. (2009). "Gompertz software reliability model: estimation algorithm and empirical validation". Journal of Systems and Software . 82 (3): 535–543. doi :10.1016/j.jss.2008.11.840 . ↑ Bemmaor, Albert C.; Glady, Nicolas (2012). "Modeling Purchasing Behavior With Sudden 'Death': A Flexible Customer Lifetime Model" . Management Science . 58 (5): 1012–1021. doi :10.1287/mnsc.1110.1461 . ↑ Bauckhage, C. (2014), Characterizations and Kullback-Leibler Divergence of Gompertz Distributions , arXiv:1402.3193 .








![{\displaystyle \left(1/b\right)\ln \left[\left(-1/\eta \right)\ln \left(1/2\right)+1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/623a5afbfea7882950bb48b5407792fa691b138f)




![{\displaystyle +\left(\pi ^{2}/6\right)+2\gamma \ln \left(\eta \right)+[\ln \left(\eta \right)]^{2}-e^{\eta }[{\text{Ei}}\left(-\eta \right)]^{2}\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0850883c7b5814914301c155e014ceb896b962b7)

![{\displaystyle {\begin{aligned}{\text{ and }}{}_{3}{\text{F}}_{3}&\left(1,1,1;2,2,2;-z\right)=\\&\sum _{k=0}^{\infty }\left[1/\left(k+1\right)^{3}\right]\left(-1\right)^{k}\left(z^{k}/k!\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/119de9d74e9e1513410d20f25e74f7b7336a0948)









![{\displaystyle {\begin{aligned}D_{KL}(f_{1}\parallel f_{2})&=\int _{0}^{\infty }f_{1}(x;b_{1},\eta _{1})\,\ln {\frac {f_{1}(x;b_{1},\eta _{1})}{f_{2}(x;b_{2},\eta _{2})}}dx\\&=\ln {\frac {e^{\eta _{1}}\,b_{1}\,\eta _{1}}{e^{\eta _{2}}\,b_{2}\,\eta _{2}}}+e^{\eta _{1}}\left[\left({\frac {b_{2}}{b_{1}}}-1\right)\,\operatorname {Ei} (-\eta _{1})+{\frac {\eta _{2}}{\eta _{1}^{\frac {b_{2}}{b_{1}}}}}\,\Gamma \left({\frac {b_{2}}{b_{1}}}+1,\eta _{1}\right)\right]-(\eta _{1}+1)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f9b95f1a065a165b2d14d8e118ed769dc59be0d)

