پاسخ فرکانسی
پاسخ فرکانسی (به انگلیسی: frequency response) در الکترونیک، اندازه کمی طیف خروجی یک سیستم یا دستگاه در جواب به یک محرک است، از پاسخ فرکانسی برای ویژگیپردازی پویایی سامانه استفاده میشود. این مفهوم مقیاسی از «بزرگی و فاز» خروجی به عنوان تابعی از فرکانس در مقایسه با ورودی است. برای یک سامانه خطی، دو برابر کردن دامنه ورودی منجر به دو برابر کردن دامنه خروجی میشود، و جمعکردن دو ورودی منجر به ایجاد یک خروجی میشود که مجموع دو خروجی متناظر برای ورودیهای منفرد است. به علاوه، اگر سامانه تغییرناپذیر با زمان (یا LTI) باشد، آنوقت جواب فرکانسی نیز با زمان تغییر نمیکند، و تزریق یک موج سینوسی به سامانه که دارای فرکانس معین است، باعث میشود که سامانه با همان فرکانس مشابه با اندازه معین و زاویه فاز معین مرتبط با ورودی پاسخگو شود. از این رو برای سامانههای LTI، پاسخ فرکانسی را میتوان به صورت اعمال تابع انتقال سامانه به یک آرگومان عددی فقط موهومی که نشاندهنده فرکانس تحریک سینوسی است، تصور نمود.[۱]
دو کاربرد تحلیل پاسخ فرکانسی با هم مرتبط اند ولی اهداف متفاوتی دارند. اول، برای یک سامانه صوتی، هدف میتواند بازتولید سیگنال ورودی به صورت بدون اعوجاج باشد. این موضوع میتواند به یک اندازه پاسخ یکسان (هموار) برای محدوده پهنایباند سامانه نیاز داشته باشد، که سیگنال دقیقاً به یک مقدار زمانی مشابه در همه فرکانسها تأخیر دارد. میزان زمان میتواند ثانیه، یا هفته یا ماه در مورد حالت رسانه ذخیرهشده باشد. در مقابل، برای یک وسیله بازخورد که از آن برای کنترل یک سامانه پویا استفاده میشود، هدف میتواند ایجاد پاسخ بهبودیافته سامانه حلقه-بسته در مقایسه با سامانه جبراننشده باشد. بازخورد عموماً نیاز به پاسخگویی به پویایی سامانه در تعداد بسیار اندکی چرخه نوسان (معمولا کمتر از یک چرخه کامل)، و با یک زاویه فاز معین مرتبط با ورودی کنترلی دستوردادهشده دارد. برای بازخورد تقویت کافی، اگر زاویه فاز را اشتباه کنیم، این منجر به ناپایداری برای یک سامانه پایدار حلقه-باز، یا ناتوانی برای پایدارسازی سامانهای میشود که به صورت حلقه-باز ناپایدار است.
از فیلترهای دیجیتال هم در سامانههای صوتی و هم در سامانههای کنترل بازخورد استفاده میشود، اما به این دلیل که اهداف متفاوتی دارند، معمولاً مشخصات فاری فیلترها به صورت قابلملاحظهای برای دو کاربرد متفاوت هستند.
تخمین و ترسیم
[ویرایش]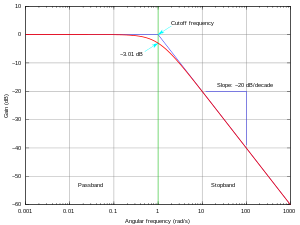
تخمین پاسخ فرکانسی برای یک سامانه فیزیکی معمولاً شامل تحریک سامانه با یک سیگنال ورودی، اندازهگیری تاریخچه زمانی هم ورودی و هم خروجی، و مقایسه این دو از طریق یک فرایند مثل تبدیل فوریه سریع (FFT) است. چیزی که باید در مورد تحلیل در ذهن داشته باشیم آن است که محتوای فرکانسی سیگنال ورودی باید برد فرکانسی مورد نظر را بپوشاند، زیرا نتایج برای بخشی از برد فرکانس که پوشانده نشده است، صادق نیست.
پاسخ فرکانسی یک سامانه را میتوان با اعمال یک «سیگنال آزمون» اندازهگیری کرد، برای مثال:
- اعمال یک ضربه به سامانه و اندازهگیری پاسخ آن (پاسخ ضربه را ببینید)
- یک آهنگ خالص با دامنه-ثابت را در سرتاسر پهنایباند مورد نظر جاروب کرد، و مرحله و جابجایی فاز خروجی مرتبط با ورودی را اندازهگیری کرد
- اعمال یک طیف با فرکانس پهن (برای مثال سیگنالهای چندفرکانسی[۲] (تسهیم فرکانس-گسسته غیرمتعامد برای سیگنالها(N-OFDM[۳][۴] یا به صورت مشابه SEFDM[۵]) و OFDM) نویز با دنباله طول حداکثری که به صورت دیجیتالی ایجاد شده است، یا معادل نویز سفید به صورت آنالوگ فیلتر شده، مثل نویز صورتی) و محاسبه پاسخ ضربه با واهمگشت برای این سیگنال ورودی و سیگنال خروجی در سامانه
پاسخ فرکانسی توسط اندازه پاسخ سامانه مشخص میشود، که معمولاً در دسیبل (dB) یا به صورت دهدهی و فاز اندازهگیری شده در رادیان یا زاویه، در برابر فرکانس است که واحد رادیان\ثانیه یا هرتز (Hz) دارد.
این اندازهگیریهای پاسخ را میتوان به سه شیوه ترسیم کرد: ترسیم اندازهگیریهای اندازه و فاز در دو نمودار مستطیلی به عنوان تابعی از فرکانس تا به یک نمودار بود برسیم؛ با ترسیم اندازه و زاویه فاز در یک نمودار قطبی منفرد با پارامتر فرکانس تا به یک نمودار نایکوئیست برسیم؛ یا با ترسیم اندازه و فاز در یک نمودار مستطیلی منفرد با پارامتر فرکانس تا به یک نمودار نیکولز برسیم.
برای سامانههای صوتی با تأخیر زمانی یکنواخت در همه فرکانسها، قسمت اندازه در برابر فرکانس نمودار بود میتواند همه آن چیزی باشد که مورد نظر و علاقه ما است. برای طراحی سامانههای کنترلی، از هر کدام از سه نوع نمودار (بود، نیکویست، نیکولز) میتوان استفاده کرد تا پایداری حلقه-بسته و پایداری حاشیهای (حاشیه نفع و فاز) را از پاسخ فرکانسی حلقه-باز استنتاج کنیم، با این شرط که برای تحلیل بود، نمودار فاز-دربرابر-فرکانس را شامل کنیم.
حالت پاسخ فرکانسی برای سامانههای دیجیتالی (مثل فیلترهای FFT) دورهای است و چندین لوب اصلی و لوبکناری دارد.[۶]
پاسخ فرکانسی غیرخطی
[ویرایش]اگر سامانه مورد بررسی غیرخطی باشد، آنگاه اعمال تحلیل دامنه فرکانس صرفاً خطی همه مشخصههای غیرخطی را آشکار نمیکند. برای غلبه بر این محدودیتها، توابع پاسخ فرکانسی تعمیمیافته و توابع پاسخ فرکانسی خروجی غیرخطی تعریف شده است که به کاربر امکان تحلیل تأثیرات پویای غیرخطی پیچیده را میدهد.[۷] روشهای پاسخ فرکانسی غیرخطی، تأثیرات تشدید مختلط، میانمدگرایی، و انتقال انرژی را آشکار میکند، که این تأثیرات را نمیتوان به کمک یک تحلیل صرفاً خطی مشاهده نمود، و این موارد در جهان غیرخطی به صورت فزاینده در حال مهم شدن هستند.
کاربردها
[ویرایش]در الکترونیک این محرک میتواند یک سیگنال ورودی باشد.[۸] در محدوده قابل شنیدن این موضوع معمولاً در ارتباط با تقویتکننده الکترونیکی، میکروفنها، و بلندگوها به آن رجوع میشود. پاسخ فرکانسی طیف رادیویی با اندازهگیریهای کابل هممحور، کابل دوتایی بافته، و تجهیزات تعویض ویدئو، ابزارهای ارتباطی بیسیم، و سامانههای آنتنی مرتبط است. اندازهگیریهای پاسخ فرکانسی زیرصوت شامل زلزله و نوار مغزی (امواج مغزی) است.
نیازمندی پاسخ فرکانسی بر اساس کاربرد متفاوت هستند.[۹] در صوت پس همانده، یک تقویتکننده به یک پاسخ فرکانسی با ۲۰ تا ۲۰٬۰۰۰ هرتز با تحمل تقریبی ±۰٫۱ دسیبل در فرکانسهای برد-میانی حدوداً ۱۰۰۰ هرتز احتیاج دارد؛ با این حال در مکالمه راهدور یک پاسخ فرکانسی با ۴۰۰ تا ۴۰۰۰ هرتز با تحمل ±۱ دسیبل برای قابل فهم بودن سخن کافی است.[۹]
از منحنیهای پاسخ فرکانسی معمولاً برای نشاندادن دقت مولفهها و سامانههای الکترونیکی استفاده میشود.[۸] وقتیکه یک سامانه یا مولفه همه سیگنالهای ورودی مورد نیاز را بدون تقویت یا تضعیف یک باند فرکانسی خاص بازتولید کند، به آن سامانه یا مولفه «صاف» گفته میشود، یا اینکه آن سامانه یا مولفه یک منحنی پاسخ فرکانسی صاف دارد.[۸] در حالت دیگر میتوان از حالت ۳ بعدی سطح پاسخ فرکانسی استفاده کرد.
موقعی که یک پاسخ فرکانسی اندازهگیری شد، (مثلا به صورت یک پاسخ ضربه)، اگر سامانه خطی و تغییرناپذیر با زمان باشد، مشخصه آن را میتوان با دفت اختیاری بوسیله یک فیلتر دیجیتال تقریب زد. به صورت مشابه، اگر نشان داده شود که سامانه پاسخ فرکانسی ضعیفی دارد، میتوان یک فیلتر دیجیتال یا آنالوگ را به سیگنالها قبل از بازتولیدشان اعمال کرد تا این کمبودها را جبران نمود.
حالت منحنی پاسخ فرکانسی برای محافظت ضد-اختلال رادارها، ارتباطات و دیگر سامانهها بسیار مهم است.
پاسخ فرکانسی یک سیستم عبارت است از پاسخ آن به تحریکهای اِعمالشده در فرکانسهای مختلف، پس از چشمپوشی از پاسخ گذرای سیستم.
از نظر ریاضی، پاسخ فرکانسی سیستم برابر است با نسبت طیف فرکانسی خروجی (پاسخ) سیستم به طیف فرکانسی ورودی (تحریک) آن. از دیدگاهی دیگر، پاسخ فرکانسی سیستم، تبدیل فوریهٔ پاسخ ضربهٔ آن است.
پاسخ فرکانسی سیستم، در حالت کلی، تابعی مختلط است که دامنه (قدر مطلق) و فاز آن با فرکانس تغییر میکند.
در سادهترین تعریف، اگر یک تحریک (ورودی) سینوسی با دامنه، فرکانس و فازی معیّن به یک سیستم خطی اِعمال شود، این سیستم در همان فرکانس پاسخ خواهد داد، بهطوریکه دامنه و فاز پاسخ (خروجی) سیستم به این تحریک، بر اساس پاسخ فرکانسی سیستم، قابل تعیین خواهد بود. اگر سیستم تغییرناپذیر با زمان باشد، پاسخ فرکانسی نیز با زمان تغییر نخواهد کرد.
چهبسا هدف سیستمهای صوتی، بازتولید سیگنال ورودی بدون بروز هرگونه اعوجاج هارمونیکی در آن باشد. به این منظور، پاسخ فرکانسی یک سیستم صوتی ایدهآل میبایست دارای دامنهٔ (قدر مطلق پاسخ فرکانسی) ثابتی در محدودهٔ فرکانسهای صوتی (حدود ۲۰ هرتز تا ۲۰ کیلوهرتز) باشد. از سوی دیگر، فاز پاسخ فرکانسی سیستم در این محدوده هم میبایست بهطور خطی با فرکانس تغییر کند تا همهٔ فرکانسهای سیگنال صوتی به یک میزان دچار تأخیر شوند.
منابع
[ویرایش]- ↑ Dennis L. Feucht (1990). Handbook of Analog Circuit Design. Elsevier Science. p. 192. ISBN 978-1-4832-5938-3.
- ↑ «Espacenet - Bibliographic data». worldwide.espacenet.com. دریافتشده در ۲۰۲۴-۰۴-۰۳.
- ↑ Slyusar, V. I. Smolyar, V. G. The method of nonorthogonal frequency-discrete modulation of signals for narrow-band communication channels// Radio electronics and communications systems c/c of Izvestiia- vysshie uchebnye zavedeniia radioelektronika. – 2004, volume 47; part 4, pages 40–44. – Allerton press Inc. (USA)[۱]
- ↑ Slyusar, V. I. Smolyar, V. G. Multifrequency operation of communication channels based on super-Rayleigh resolution of signals// Radio electronics and communications systems c/c of Izvestiia- vysshie uchebnye zavedeniia radioelektronika.. – 2003, volume 46; part 7, pages 22–27. – Allerton press Inc. (USA)[۲]
- ↑ M. R. D. Rodrigues and I. Darwazeh. A Spectrally Efficient Frequency Division Multiplexing Based Communications System.// InOWo'03, 8th International OFDM-Workshop, Proceedings, Hamburg, DE, September 24–25, 2003. – https://www.researchgate.net/publication/309373002
- ↑ L. R. Rabiner and B. Gold. Theory and Application of Digital Signal Processing. – Englewood Cliffs, NJ: Prentice-Hall, 1975. – 720 pp
- ↑ Billings S.A. "Nonlinear System Identification: NARMAX Methods in the Time, Frequency, and Spatio-Temporal Domains". Wiley, 2013
- ↑ ۸٫۰ ۸٫۱ ۸٫۲ Stark, 2002, p. 51.
- ↑ ۹٫۰ ۹٫۱ Luther, 1999, p. 141.
مشارکتکنندگان ویکیپدیا. «Frequency response». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۱۴ اکتبر ۲۰۲۱.
مشارکتکنندگان ویکیپدیا. «Frequency response». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۲۳ دسامبر ۲۰۰۸. منبع:ویکیپدیا به زبان انگلیسی
