رادیان

در همهٔ موارد عملی، زاویه بر حسب واحدهایی اندازه‌گیری می‌شود که از تقسیم زاویهٔ راست (قائم) به اجزاء برابر به دست می‌آیند. اگر تعداد این اجزا ۹۰ باشد، واحد همان واحد آشنای درجه است. تقسیم زاویهٔ راست به ۱۰۰ جزء برای نظام اعشاری ما مناسب‌تر است (واحد گرادیان)، ولی آن هم معرف همین شیوهٔ اندازه‌گیری است. اما در بررسی‌های نظری بهتر است برای مشخص کردنِ اندازهٔ زاویه، از شیوهٔ اساساً متفاوتی استفاده کنیم که آن را اندازهٔ رادیانی یا اندازه بر حسب رادیان می‌نامند.

بسیاری از فرمول‌های مهمی که شامل تابع‌های مثلثاتیِ زاویه‌ها هستند، در این نظام شکل ساده‌تری دارند تا در نظام اندازه‌گیری بر حسب درجه.

کمانی از دایره با طول برابر با شعاع دایره متناظر است با زاویهٔ ۱ رادیان. دایرهٔ کامل متناظر است با $2\pi$ رادیان.

کمانی که اندازه آن با شعاع دایره برابر است

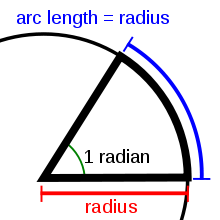
رادیان زاویه مرکزی مقابل به کمانی از دایره است که طول آن با شعاع دایره برابر است؛ یعنی زاویه مرکزیِ متناظر با محیط دایره، مساویِ $2\pi$ رادیان و اندازه زاویه نیم صفحه، $\pi$ رادیان و اندازه زاویه قائمه، $\pi /2$ رادیان است.

اندازهٔ بر حسب رادیان برای عملیات تحلیلی و نظری مناسب ولی برای استفاده‌های عملی نسبتاً نامناسب است، چون عدد $\pi$ گنگ است. اگر از نقطه‌ای روی دایره شروع کرده پشت سر هم کمان‌های واحد یعنی کمان‌هایی به اندازهٔ ۱ رادیان جدا کنیم، هرگز به نقطهٔ شروع باز نخواهیم گشت. اما نظام اندازه‌گیری معمولی طوری طراحی شده که پس از ۳۶۰ بار کمان یک درجه‌ای، به نقطهٔ شروع برمی‌گردیم. (یعنی یک دور به ۳۶۰ واحد صحیح تقسیم شده‌است.)

علت وجود رادیان

می‌دانیم که درجه واحدی برای اندازه‌گیری زاویه است. یک دایرهٔ کامل برابر با ۳۶۰ درجه، نیم دایره برابر با ۱۸۰ درجه و ربع دایره برابر با ۹۰ درجه است.

اما تا به حال از خود پرسیده‌اید چرا یک دایرهٔ کامل را ۳۶۰ درجه می‌گوییم؟ علت چیست؟

واحد درجه از زمان‌های بسیار دور هم وجود داشته و در واقع نوعی قرارداد است. اینکه چرا مردمان گذشته، یک درجه را برابر با یک ۳۶۰ام دایره گرفته‌اند، معلوم نیست.

البته نظراتی دربارهٔ تاریخچهٔ آن بیان شده: برخی بر این عقیده‌اند که در گذشته، اخترشناسان گمان می‌بردند که خورشید در هر روز به اندازهٔ ۱/۳۶۰ (یک ۳۶۰ام) محیط دایره جابجا می‌شود. به همین دلیل یک درجه را بدین صورت تعریف کردند.

نظر دیگری می‌گوید که بابلی‌ها این واحد را اختراع کرده‌اند؛ واحد شمارش بابلی‌ها بر مبنای ۶۰ بوده (در حال حاضر بر مبنای ۱۰ است)؛ به همین دلیل به عدد ۳۶۰ رسیده‌اند.

همان‌طور که می‌بینید، درجه مبنای مشخصی ندارد. دانشمندان به این موضوع پی‌برده بودند. به همین دلیل سعی کردند واحدی برای زاویه بیابند که عمومی باشد؛ در نتیجه رادیان به وجود آمد. پس رادیان واحدی کاربردی‌تر برای اندازه‌گیری زاویه است.

معنی لغوی رادیان

رادیان واحد مسافت بر حسب واحد شعاع است و به نظر می‌رسد که رادیان ترکیبی از آن کلمه باشد. به بیان ساده‌تر رادیان صرفاً یک عدد مانند ۲٫۵ یا ۶۹ است و هیچ واحدی ندارد. در محاسبات، رادیان به معنی مسافت طی شده تقسیم بر شعاع دایره است؛ و می‌بینیم که وقتی طول بر طول تقسیم می‌شود هر گونه واحدی از بین می‌رود. اما وقتی از دیدگاه عملی، رادیان را بررسی می‌کنیم بهتر است تصور کنیم که رادیان مسافت طی شده روی یک دایرهٔ واحد است.

تبدیل رادیان به درجه

هر رادیان تقریباً برابر با ۵۷ درجه است. به عبارت دیگر هر رادیان برابر ${\frac {180}{\pi }}$ درجه است؛ بنابراین با ضرب ${\frac {180}{\pi }}$ در رادیان، درجه به دست می‌آید. به عبارت دیگر با ضرب زاویه بر حسب رادیان در ۱۸۰ و تقسیم آن بر عدد پی، درجه به دست می‌آید.

زاویه در درجه = زاویه در رادیان . ${\frac {180}{\pi }}$

به عنوان مثال:

$1{\mbox{ rad}}=1\cdot {\frac {180^{\circ }}{\pi }}\approx 57.2958^{\circ }$

$2.5{\mbox{ rad}}=2.5\cdot {\frac {180^{\circ }}{\pi }}\approx 143.2394^{\circ }$

و بلعکس: با ضرب ${\frac {\pi }{180}}$ در درجه، رادیان به‌دست می‌آید:

$1^{\circ }=1\cdot {\frac {\pi }{180^{\circ }}}\approx 0.0175{\mbox{ rad}}$

$23^{\circ }=23\cdot {\frac {\pi }{180^{\circ }}}\approx 0.4014{\mbox{ rad}}$

جدول زیر تبدیل چند زاویه پرکاربرد را نمایش می‌دهد:

درجه	۰°	۳۰°	۴۵°	۶۰°	۹۰°	۱۸۰°	۲۷۰°	۳۶۰°
رادیان	۰	${\frac {\pi }{6}}$	${\frac {\pi }{4}}$	${\frac {\pi }{3}}$	${\frac {\pi }{2}}$	$\pi \,$	${\frac {3\pi }{2}}$	$2\pi \,$

جستارهای وابسته

• مثلثات
• گراد
• استرادیان

منابع

• Weisstein, Eric W. "Radian." From MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/Radian.html