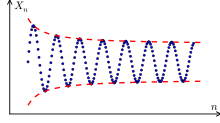
یک دنبالهٔ همگرا که به عدد خاصی میل میکند در حسابان ، حد یک دنباله مقداری است که در صورت وجود، جملههای آن دنباله با پیشروی، به قدر دلخواه به آن نزدیک میشوند؛ اگر چنین مقداری وجود داشته باشد، دنباله را همگرا و در غیر این صورت دنباله را واگرا مینامیم.[ ۱]
به حد یک دنباله در بینهایت «حد دنباله» میگویند.
در نمایش مختصاتی ، بازهٔ دوبعدی افقی حول مقدار
y
=
A
{\displaystyle y=A}
دنبالهٔ
{
a
n
}
n
=
1
∞
{\displaystyle \{a_{n}\}_{n=1}^{\infty }}
A
{\displaystyle A}
N
{\displaystyle N}
a
n
{\displaystyle a_{n}}
2
ε
{\displaystyle 2\varepsilon }
به بیان دقیقتر، برای دنبالهٔ
{
a
n
}
n
=
1
∞
{\displaystyle \{a_{n}\}_{n=1}^{\infty }}
[ ۲]
lim
n
→
∞
a
n
=
A
⟸
∀
ε
>
0
:
∃
N
∈
N
:
d
(
a
n
,
A
)
<
ε
,
∀
n
≥
N
{\displaystyle \lim _{n\to \infty }a_{n}=A\Longleftarrow \forall \varepsilon >0:\exists N\in \mathbb {N} :d(a_{n},A)<\varepsilon ,\forall n\geq N}
که
ε
{\displaystyle \varepsilon }
d
(
x
,
y
)
{\displaystyle d(x,y)}
فضای متریک به معنای فاصلهٔ
y
{\displaystyle y}
x
{\displaystyle x}
|
x
−
y
|
{\displaystyle |x-y|}
در این صورت مینویسیم:
lim
n
→
∞
a
n
=
A
{\displaystyle \lim _{n\to \infty }a_{n}=A}
نمونهای از یک دنبالهٔ واگرا که به هیچ مقداری میل نمیکند برای بعضی دنبالههای واگرا نیز عبارتی همچون
lim
n
→
∞
b
n
=
∞
{\displaystyle \lim _{n\to \infty }b_{n}=\infty }
lim
n
→
∞
b
n
=
−
∞
{\displaystyle \lim _{n\to \infty }b_{n}=-\infty }
دنبالهٔ
{
b
n
}
n
=
1
∞
{\displaystyle \{b_{n}\}_{n=1}^{\infty }}
دنبالهٔ
{
b
n
}
n
=
1
∞
{\displaystyle \{b_{n}\}_{n=1}^{\infty }}
lim
n
→
∞
b
n
=
∞
⟸
∀
B
∈
N
:
∃
N
∈
N
:
b
n
>
B
,
∀
n
≥
N
{\displaystyle \lim _{n\to \infty }b_{n}=\infty \Longleftarrow \forall B\in \mathbb {N} :\exists N\in \mathbb {N} :b_{n}>B,\forall n\geq N}
دنبالهٔ واگرای
a
n
=
(
−
1
)
n
{\displaystyle a_{n}=(-1)^{n}}
ویژگیهای حد دنباله مثل ویژگیهای حد تابع هستند.
حد دنباله در صورت وجود، یکتاست. یعنی اگر
lim
n
→
∞
a
n
=
A
1
{\displaystyle \lim _{n\to \infty }a_{n}=A_{1}}
lim
n
→
∞
a
n
=
A
2
{\displaystyle \lim _{n\to \infty }a_{n}=A_{2}}
A
1
=
A
2
{\displaystyle A_{1}=A_{2}}
[ ۲]
اگر برای دنبالهٔ
{
a
n
}
n
=
1
∞
{\displaystyle \{a_{n}\}_{n=1}^{\infty }}
lim
n
→
∞
a
n
=
A
{\displaystyle \lim _{n\to \infty }a_{n}=A}
تابع پیوستهٔ
f
{\displaystyle f}
lim
n
→
∞
f
(
a
n
)
=
lim
n
→
∞
f
(
A
)
{\displaystyle \lim _{n\to \infty }f(a_{n})=\lim _{n\to \infty }f(A)}
lim
n
→
∞
(
a
n
±
b
n
)
=
lim
n
→
∞
a
n
±
lim
n
→
∞
b
n
{\displaystyle \lim _{n\to \infty }(a_{n}\pm b_{n})=\lim _{n\to \infty }a_{n}\pm \lim _{n\to \infty }b_{n}}
lim
n
→
∞
(
c
a
n
)
=
c
lim
n
→
∞
a
n
{\displaystyle \lim _{n\to \infty }(ca_{n})=c\lim _{n\to \infty }a_{n}}
lim
n
→
∞
(
a
n
b
n
)
=
(
lim
n
→
∞
a
n
)
(
lim
n
→
∞
b
n
)
{\displaystyle \lim _{n\to \infty }(a_{n}b_{n})=(\lim _{n\to \infty }a_{n})(\lim _{n\to \infty }b_{n})}
lim
n
→
∞
(
a
n
b
n
)
=
lim
n
→
∞
a
n
lim
n
→
∞
b
n
{\displaystyle \lim _{n\to \infty }({a_{n} \over b_{n}})={\lim _{n\to \infty }a_{n} \over \lim _{n\to \infty }b_{n}}}
lim
n
→
∞
b
n
≠
0
{\displaystyle \lim _{n\to \infty }b_{n}\neq 0}
lim
n
→
∞
(
a
n
p
)
=
(
lim
n
→
∞
a
n
)
p
{\displaystyle \lim _{n\to \infty }(a_{n}^{p})=(\lim _{n\to \infty }a_{n})^{p}}
a
n
≤
b
n
⟺
lim
n
→
∞
a
n
≤
lim
n
→
∞
b
n
{\displaystyle a_{n}\leq b_{n}\Longleftrightarrow \lim _{n\to \infty }a_{n}\leq \lim _{n\to \infty }b_{n}}
[ ۳]
توجّه کنید که در بسیاری از موارد
a
n
<
b
n
{\displaystyle a_{n}<b_{n}}
lim
n
→
∞
a
n
=
lim
n
→
∞
b
n
{\displaystyle \lim _{n\to \infty }a_{n}=\lim _{n\to \infty }b_{n}}
اگر
f
:
R
⟶
R
{\displaystyle f:\mathbb {R} \longrightarrow \mathbb {R} }
f
(
n
)
=
a
n
{\displaystyle f(n)=a_{n}}
lim
n
→
∞
a
n
=
lim
n
→
∞
f
(
n
)
{\displaystyle \lim _{n\to \infty }a_{n}=\lim _{n\to \infty }f(n)}
[ ۳]
اگر از یک اندیس به بعد
b
n
≤
a
n
≤
c
n
{\displaystyle b_{n}\leq a_{n}\leq c_{n}}
lim
n
→
∞
c
n
=
lim
n
→
∞
b
n
=
L
{\displaystyle \lim _{n\to \infty }c_{n}=\lim _{n\to \infty }b_{n}=L}
lim
n
→
∞
a
n
=
L
{\displaystyle \lim _{n\to \infty }a_{n}=L}
[ ۳]
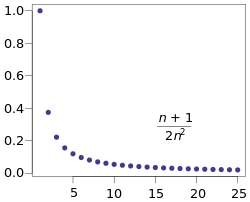
دنبالهٔ فوق نزولی ست و همیشه بیش از صفر، پس همگرا ست اگر
{
a
n
}
{\displaystyle \{a_{n}\}}
[ ۳]
α
>
0
⟹
lim
n
→
∞
1
n
α
=
0
{\displaystyle \alpha >0\Longrightarrow \lim _{n\to \infty }{1 \over n^{\alpha }}=0}
[ ۴]
|
c
|
<
1
⟹
lim
n
→
∞
c
n
=
0
{\displaystyle |c|<1\Longrightarrow \lim _{n\to \infty }c^{n}=0}
c
>
0
⟹
lim
n
→
∞
c
1
n
=
1
{\displaystyle c>0\Longrightarrow \lim _{n\to \infty }c^{1 \over n}=1}
a
>
0
,
b
>
0
⟹
lim
n
→
∞
(
log
n
)
a
n
b
=
0
{\displaystyle a>0,b>0\Longrightarrow \lim _{n\to \infty }{(\log n)^{a} \over n^{b}}=0}
lim
n
→
∞
n
1
n
=
lim
n
→
∞
n
n
=
1
{\displaystyle \lim _{n\to \infty }n^{1 \over n}=\lim _{n\to \infty }{\sqrt[{n}]{n}}=1}
a
∈
R
⟹
lim
n
→
∞
(
1
+
a
n
)
n
=
e
a
{\displaystyle a\in \mathbb {R} \Longrightarrow \lim _{n\to \infty }(1+{a \over n})^{n}=e^{a}}
c
∈
R
⟹
lim
n
→
∞
c
n
n
!
=
0
{\displaystyle c\in \mathbb {R} \Longrightarrow \lim _{n\to \infty }{c^{n} \over n!}=0}
[ ۳]















































![{\displaystyle \lim _{n\to \infty }n^{1 \over n}=\lim _{n\to \infty }{\sqrt[{n}]{n}}=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3d0e1e01d9a7ddd22f10450f2fd9f879dbf43a6)

