هرم (هندسه)

هرم مربع‌القاعده
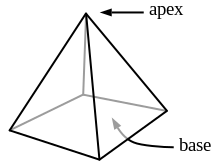مثال: هرم مربع‌القاعده
وجوه	n مثلث ۱ چندضلعی n-ضلعی
اضلاع	2n
رئوس	n + 1
نماد اشلفلی	( ) ∨ {n}
نشانه گذاری چندوجهی کانوی	Yn
گروه تقارنی	Cnv, [1,n], (*nn), order 2n
گروه چرخشی	Cn, [1,n]+, (nn), order n
چندوجهی دوگان	خود-دوگان
ویژگی‌ها	محدب

هرم شکلی سه‌بعدی است که از اتصال نقطه‌ای در فضا به تمام نقاط چند ضلعی بسته ای در صفحه به وجود می‌آید. به آن نقطه، رأس هرم و به آن چند ضلعی مسطح، قاعده هرم گفته می‌شود. قاعده هرم، چندضلعی دلخواه است و سایر وجه‌ها مثلث‌هایی همرس هستند که در رأس به یکدیگر متصل می‌شوند. خط قائمی که رأس را به قاعده متصل می‌کند، ارتفاع هرم نامیده می‌شود. از معروف‌ترین سازه‌های جهان به شکل هرم، می‌توان به اهرام ثلاثه مصر اشاره کرد.

تعریف هرم

با اتصال رئوس چند ضلعی B (قاعده) در صفحهٔ P به نقطهٔ v «هرم» تشکیل می‌شود. با برش هرم توسط صفحهٔ E موازی P «بریدهٔ هرمی» ساخته می‌شود. با قرار دادن یک هرم بر روی یک بریدهٔ هرمی، می‌توان ابلیسک ساخت.

«هرم» از گونه‌های شناخته‌شدهٔ چندوجهی است. قاعدهٔ هر کدام از اهرام مصر معمولاً مربع است و چهار وجه دیگر مثلث هستند. هرم به‌طور کلی از یک قاعدهٔ چندضلعی B واقع در صفحهٔ P تشکیل می‌شود که رئوس آن به‌وسیلهٔ وجه‌های مثلثی‌شکل به نقطهٔ v که روی صفحهٔ P نیست متصل شده‌اند. با این حساب یال M هر هرم، سطحی چندوجهی با وجوه مثلثی خواهد بود. برای ساختن یک هرم می‌توان از اکستروژن مرکزی بهره برد. در اکستروژن مرکزی رئوس چندضلعی B در صفحهٔ p در راستای خطوط متصل‌کننده به سوی یک نقطه (v) کشیده می‌شوند و شکل نهایی هرم به شکل چندضلعی B و جای نقطهٔ v وابسته است.

با برش زدن هرم توسط صفحهٔ E موازی با صفحهٔ P «بریدهٔ هرمی» ایجاد می‌شود. پایهٔ ابلیسک نمونهٔ یک بریدهٔ هرمی است.

انواع هرم

ساختمان هرمی دانشگاه ایالتی کالیفرنیا در لانگ بیچ

اگر قاعده هرم مثلث یا مربع باشد به آن، به ترتیب، هرم مثلث‌القاعده و هرم مربع‌القاعده می‌گویند. اگر قاعده هرم (یا شکل هرمی) دایره باشد به آن مخروط گفته می‌شود.

حجم هرم

حجم درون یک هرم برابر یک سوم مساحت قاعده، ضرب در ارتفاع هرم است که منظور از ارتفاع هرم فاصله رأس تا صفحه‌ای است که قاعده در آن قرار دارد؛ بنابراین:

${1 \over 3}Sh$

که در آن S مساحت قاعده و h ارتفاع هرم هستند.

اگر یک منشور را به سه هرم تجزیه کنیم، حجم هر سه هرم با هم برابر خواهد بود. پس می‌توان نتیجه گرفت که حجم هر هرم برابر با یک سوم حجم منشوری است که با همان قاعده و همان ارتفاع ساخته خواهد شد.

منابع

• مشارکت‌کنندگان ویکی‌پدیا. «هرم (هندسه)». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۳۰ دی ۱۳۹۱.