درگاه:ریاضیات
درگاههای ویکیپدیا: فرهنگ · جغرافیا · بهداشت و درمان · تاریخ · ریاضیات · علوم طبیعی · مردم · فلسفه · دین · اجتماعی · فناوری
|
درگاه ریاضیات ریاضیات (Mathematics) را معمولاً دانش بررسی کمیتها و ساختارها و فضا و تبدیل تعریف میکنند. دیدگاه دیگری ریاضی را دانشی میداند که در آن با استدلال منطقی از اصول و تعریفها به نتایج دقیق و جدیدی میرسیم. دیدگاههای دیگری نیز در فلسفه ریاضیات بیان شدهاست. اگرچه ریاضیات خود یکی از علوم طبیعی بهشمار نمیرود ولی ساختارهای ویژهای که ریاضیدانان میپژوهند، بیشتر از دانشهای طبیعی به ویژه فیزیک سرچشمه میگیرند و در فضایی جدا از طبیعت و محضگونه گسترش پیدا میکند به طوری که علوم طبیعی برای حل مسائل خود به ریاضی باز میگردند تا جوابشان را با آن مقایسه و بررسی کنند. علوم طبیعی، مهندسی و اقتصاد، بسیار به ریاضیات تکیه دارند. آن بخش از ریاضیات را که علوم کاربردی به آن بیشتر میپردازند، ریاضیات کاربردی مینامند. ولی گاه ریاضیدانان به دلایل صرفاً ریاضی و نه کاربردی به تعریف و بررسی برخی ساختارها میپردازند که به آن ریاضیات محض گفته میشود. نوشتار برگزیده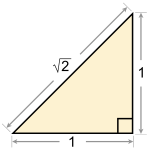 هندسه مطالعهٔ انواع روابط طولی و اشکال و خصوصیات آنها است. این دانش همراه با حساب یکی از دو شاخهٔ قدیمی ریاضیات است. واژهٔ هندسه، عربی شدهٔ واژهٔ «اندازه» در فارسی است. در زبان انگلیسی به آن geometry و در زبان فرانسه به آن géométrie میگویند که هر دو از γεωμετρία (گئومتریا) در زبان یونانی آمده که به معنای اندازهگیری زمین است. احتمالاً بابلیان و مصریان کهن نخستین کسانی بودند که اصول هندسه را کشف کردند. مصریان روش علامتگذاری زمینها با تیرک و طناب را ابداع کردند. در آغاز هندسه بر پایهٔ دانستههای تجربی پراکندهای در مورد طول و زاویه و مساحت و حجم قرار داشت که برای مساحی و ساختمان و نجوم و برخی صنایع دستی لازم میشد. بعضی از این دانستهها بسیار پیشرفته بودند مثلاً هم مصریان و هم بابلیان قضیه فیثاغورث را ۱۵۰۰ سال قبل از فیثاغورث میشناختند. زندگینامهٔ برگزیده لئوناردو دا وینچی دانشمند و هنرمند ایتالیایی دوره رنسانس است که در رشتههای نقاشی، ریاضی، معماری، موسیقی، کالبدشناسی، مهندسی، تندیسگری، و هندسه برجسته بود.
داوینچی را کهنالگوی «فرد رنسانسی» دانستهاند. وی فردی بینهایت خلاق و کنجکاو بود.او طرحهای مبتکرانهای را برای ساخت سلاحهایی مانند توپهای بخار، ماشینهای پرنده و ادوات زرهی ارائه کرده بود، هرچند که بسیاری از آنها هرگز ساخته نشدند.
داوینچی اولین طراح هواپیما و صدها اثر معماری دیگر بهشمار میرود. یکی از طرحهای ابتکاری او لباس غواصی و زیر دریایی جنگی است. او همچنین مسلسل، تانک نظامی، ساعتی که به ساعت داوینچی معروف است، کیلومتر شمار و چیزهای دیگر را طراحی یا اختراع کرد.
مفاهیم تابع یکی از مفاهیم نظریه مجموعهها و حساب دیفرانسیل و انتگرال است. بطور ساده میتوان گفت که به قاعدههای تناظری که به هر ورودی خود یک و فقط یک خروجی نسبت میدهند، تابع گفته میشود. تابع به عنوان مفهومی در ریاضیات، توسط گوتفرید لایبنیتس در سال ۱۶۹۴، با هدف توصیف یک کمیت در رابطه با یک منحنی مانند شیب یک نمودار در یک نقطه خاص به وجود آمد. امروزه به توابعی که توسط لایبنیز تعریف شدند، توابع مشتقپذیر میگوییم. نوشتارهای برگزیدهنگارهٔ برگزیده فراکتال مندلبرو یک فراکتال سهبعدی از مجموعه مندلبرو میباشد که بوسیله دانیل وایت و پاول نایلاندر ساخته شدهاست. این فراکتال با استفاده از دستگاه مختصات کروی حاصل میگردد. گفتاورد«تا وقتی که در فیزیک اثباتهای ریاضی وجود دارد نیازی به آزمایش نداریم.» هندسه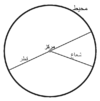 دایره مکان هندسی نقاطی از صفحه است که فاصلهشان از نقطهٔ ثابتی واقع در آن صفحه، مقدار ثابتی باشد. نقطهٔ ثابت، «مرکز دایره»، و مقدار ثابت، «اندازهٔ شعاع دایره» نامیده میشود. در حقیقت، دایره یک بیضی است که کانونهای آن بر همدیگر منطبقاند. آیا میدانستید؟ ... که به گریگوری پرلمان ریاضیدان، در 2006 جایزه فیلدز پیشنهاد شد، که بخشی از آن به خاطر اثباتی بود که او برای حدس پوانکاره ارائه داد، اما او این جایزه را رد کرد؟
|

![{\displaystyle {\begin{aligned}&\scriptstyle f\colon [-1,1.5]\to [-1,1.5]\\&\textstyle x\mapsto {\frac {(4x^{3}-6x^{2}+1){\sqrt {x+1}}}{3-x}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/367545798d4c1d7748410deb9d03ea9faf400d6d)