کنترل‌پذیری شبکه

کنترل یک شبکه ساده.

کنترل پذیری شبکه، درمورد کنترل پذیری ساختاری یک شبکه است. کنترل پذیری قابلیت ما برای هدایت یک سامانه پویا، از هر حالت اولیه، به هر حالت پایانی دلخواه، با یک انتخاب مناسب از ورودی ها، در زمان متناهی را شرح می‌دهد. این تعریف، با تصور مااز کنترل تطابق دارد. کنترل پذیری شبکه های پیچیده ی جهت دار و وزن دار کلی، اخیرا موضوع بحث جدی تعدادی از گروه ها در شبکه های متنوعی در سطح جهانی بوده است. تحقیقات اخیر توسط شارما و همکاران روی شبکه‌های زیستی چند نوعی، (شبکه های تعاملی ژن-ژن، ریزآران ای-ژن، پروتئین-پروتئین) اهداف کنترلی در استئوسارکوما شاخص فنوتیپی را تشخیص داد، که نقش مهم ژن ها و پروتئین های مسئول نگهداری ریز محیط تومور را نشان داد.

پیش زمینه

داینامیک های زمان-پایدار خطی استاندارد روی شبکه پیچیده ${\dot {\mathbf {X} }}(t)=\mathbf {A} \cdot \mathbf {X} (t)+\mathbf {B} \cdot \mathbf {u} (t)$ را در نظر بگیرید، که در آن بردار $\mathbf {X} (t)=(x_{1}(t),\cdots ,x_{N}(t))^{\mathrm {T} }$ حالت یک سیستم از $N$ راس در زمان $t$ را اختیار می‌کند. ماتریس $N\times N$ ، $\mathbf {A}$، نمودار سیم کشی سیستم و قدرت برهم کنش بین اجزا را توصیف می کند. ماتریس $N\times M$ ، $\mathbf {B}$، راس های کنترل شده توسط یک کنترل کننده ی خارجی را مشخص می کند. سیستم توسط بردار ورودی وابسته به زمان$\mathbf {u} (t)=(u_{1}(t),\cdots ,u_{M}(t))^{\mathrm {T} }$، که کنترل کننده بر سیستم تحمیل می‌کند، کنترل می‌شود. برای تشخیص کمینه تعداد رئوس راهبر که با نماد $N_{\mathrm {D} }$ نمایش داده می شود، که کنترل آن برای کنترل کامل دینامیک های سیستم کافی است، لیو و همکاران تلاش کردند که ابزارهای نظریه کنترل ساختاری را با نظریه گراف و فیزیک آماری ترکیب کنند. آنها نشان دادند که کمینه تعداد ورودی یا رئوس راهبر مورد نیاز برای اعمال کنترل کامل بر روی شبکه، با بیشینه تعداد تطابق در شبکه تعیین می‌شود، که همان بیشینه مجموعه ای از یال هاست که راس ابتدا و انتها مشترک ندارند. از این نتیجه یک قالب تحلیلی بر پایه توزیع درجه ورود خروج ایجاد شد تا $n_{\mathrm {D} }=N_{\mathrm {D} }/N$ را برای گراف های مقیاس آزاد و اردوش-رنیی پیش بینی کند. هرچند اخیرا نشان داده شده که کنترل پذیری شبکه (دیگر روشهای تنها-ساختار که فقط همبندی گراف را استفاده می کنند، $\mathbf {A}$ ، برای ساده سازی دینامیک های اصولی)، از تعداد و انتخاب مجموعه های راس های راهبر که به بهترین وجه دینامیک های شبکه را کنترل می کنند، هم فرو جهش می کند هم اضافه جهش، که اهمیت افزونگی (مانند کانالیزه کردن) و دینامیک های غیرخطی در تعیین کنترل را برجسته می‌کند.

قابل ذکر است که فرمول بندی لیو و همکاران مقادیر یکسانی را برای ${n_{\mathrm {D} }}$ گراف زنجیری و گراف همبند تنک پیش بینی می کند. به وضوح هر دو این گراف ها توزیع درجه ورود و خروج بسیار متفاوتی دارند. یک کار منتشر نشده اخیر، بررسی می‌کند که آیا درجه، که صرفاً یک مقیاس موضعی در شبکه هاست، می تواند کنترل پذیری را به طور کامل شرح دهد و آیا حتی رئوس کم فاصله هم نقشی در تعیین کنترل پذیری شبکه ندارند. در واقع برای بسیاری از شبکه‌های دنیای واقعی به عنوان مثال، شبکه غذا، شبکه عصبی و شبکه متابولیک، عدم تطابق مقادیر ${n_{\mathrm {D} }}^{real}$ و ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ محاسبه شده توسط لیو و همکارانقابل توجه است. اگر کنترل پذیری صرفاً توسط درجه مشخص شود، چرا مقادیر ${n_{\mathrm {D} }}^{real}$ و ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ برای شبکه‌های دنیای واقعی بسیاری متفاوت اند. آنها استدلال کردند که این ممکن است به دلیل تاثیر همبستگی درجه باشد. هر چند نشان داده شده است که کنترل پذیری شبکه می تواند تنها با استفاده از مرکزی میانی و مرکزی نزدیکی تغییر یابد، بدون استفاده از درجه یا همبستگی درجه.

نمودار طرح واره فوق، کنترل یک شبکه جهت دار را نشان می‌دهد. برای شبکه جهت دار داده شده، می توان بیشینه تطابق آن را که عبارت است از، بزرگترین مجموعه از یال ها، بدون راس ابتدایی یا انتهای مشترک، محاسبه کرد. تطابق بیشینه از یک مجموعه از دور ها و مسیر های جهت دار راس-مجزا تشکیل میشود. (یال های قرمز رنگ در شکل b.)اگر یک راس، راس ابتدایی یک یال تطابق باشد، آنگاه این راس تطابق داده شده است. (راس های سبز رنگ در شکل b.)در غیر این صورت بدون تطابق است.(راس های سفید رنگ در شکل b.)آن راس های بدون تطابق، راس هایی هستند که باید کنترل شوند، یعنی رئوس راهبر. با ارسال سیگنال به آن راس های راهبر، یک مجموعه از مسیر های جهت دار با این ورودی ها به عنوان راس ابتدایی بدست می‌آید.( شکل c را ببینید.)آن مسیرها “ساقه” نام دارند. گراف حاصل، ارتباط تعاملی U-ریشه‌ ای نام دارد. با “پیوند دادن” دورهای جهت دار به آن “ساقه ها”، "جوانه ها" حاصل می‌شوند. گراف حاصل کاکتوس نام دارد.( شکل d را ببینید.) طبق قضیه کنترل ساختاری، چون یک ساختار کاکتوس، شبکه کنترل شده را پوشش می‌دهد، (شکل e را ببینید.) سیستم کنترل پذیر است. ساختار کاکتوس،( شکل d.) که زیرساخت شبکه کنترل شده (شکل e.) است، "اسکلتی" برای حفظ کنترل پذیری است.

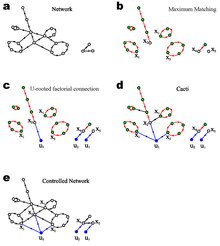
کنترل پذیری ساختاری

مفهوم خواص ساختاری ابتدا توسط لین(1974) معرفی شدند و سپس توسط شیلدز و پیرسن (1976) توسعه یافته و به تدریج توسط گلوور و سیلورمن (1976) به دست آمد. سوال اصلی این است که آیا فقدان کنترل پذیری یا مشاهده پذیری با توجه به پارامترهای متغیر، عمومی هستند. در قالب کنترل ساختاری، پارامترهای سیستم، یا متغیر های آزاد مستقل هستند یا صفر ثابت. این برای مدل‌های سیستم های فیزیکی ثابت است چون مقادیر پارامترها هیچ وقت به طور دقیق مشخص نیستند، به جز مقادیر صفر که فقدان اثر متقابل یا اتصالات را بیان می کنند.

بیشینه تطابق

در نظریه گراف یک تطابق مجموعه‌ای از یال هاست که راس مشترک ندارند. لیو و همکاران این تعریف را به گراف های جهت دار توسعه دادند که در آن یک تطابق، یک مجموعه از یال‌های جهت دار است که در ابتدا و انتها مشترک نیستند. به راحتی قابل بررسی است که یک تطابق از یک گراف جهت دار، یک مجموعه از دور ها و مسیر های ساده ی راس مجزا را تشکیل می دهد. تطابق بیشینه برای یک شبکه جهت دار، می‌تواند به طور کارآمد، با کار کردن درنمایش دو بخشی با استفاده از الگوریتم هاپکرافت-کارپ کلاسیک که در بدترین حالت در زمان O(E√N) اجرا می‌شود، محاسبه شود. برای گراف های بدون جهت، جواب های تحلیلی برای اندازه و تعداد تطابق های بیشینه با استفاده از روش کاواک که در فیزیک آماری توسعه یافته اند، برسی شده اند. لیو و همکاراناین محاسبات را برای گراف های جهت دار توسعه دادند.

با محاسبه تطابق بیشینه محدوده وسیعی از شبکه های واقعی، لیو و همکاران ادعا کردند که تعداد راس های راهبر غالباً توسط توزیع درجه شبکه هاP(k_in,k_out) تعیین می شود. آنها همچنین با استفاده از روش کاواک، میانگین تعداد راس های راهبر را برای یک گروه شبکه با توزیع درجه دلخواه محاسبه کردند. جالب است که برای گراف زنجیری و گراف همبند تنک که هر دو دارای توزیع های درجه ورود و خروج بسیار متفاوتی هستند; فرمول‌بندی لیو و همکاران مقادیری یکسانی از ${n_{\mathrm {D} }}$ را پیش‌بینی می‌کند. همچنین، برای بسیاری از شبکه های دنیای واقعی، مثل چرخه غذا، شبکه عصبی و شبکه متابولیک، عدم تطابق در مقادیر ${n_{\mathrm {D} }}^{real}$ و ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ محاسبه شده توسط لیو و همکاران، قابل توجه است. اگر کنترل پذیری تنها توسط درجه تعیین شود، چرا مقادیر ${n_{\mathrm {D} }}^{real}$ و ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ برای بسیاری از شبکه‌های دنیای واقعی اینقدر متفاوت هستند؟ هنوز قابل بررسی است که آیا توانمندی کنترل در شبکه ها، بیشتر با استفاده از مرکزی میانی و مرکزی نزدیکی تاثیر می‌پذیرد تا از درجه مقیاس های درجه محور.

با اینکه گراف‌های تنک سخت تر کنترل می شوند، به وضوح جالب خواهد بود که در یابیم آیا مرکزی میانی و مرکزی نزدیکی نقش مهمتری در تعیین کنترل پذیری گراف های تنک با توضیع درجه تقریباً یکسان دارند، یا عدم تجانس درجه.

کنترل سیستم های کوانتوم مرکب و نظریه گراف جبری

یک نظریه کنترل شبکه ها نیز در زمینه ی کنترل همگانی سیستم‌های کوانتوم مرکب توسعه یافته است که در آن زیر سیستم ها و اثر متقابل شان، به ترتیب به راس ها و لینک ها مرتبط می‌شوند. این قالب اجازه می دهد که معیار کالمان را با ابزار نظریه گراف جبری به وسیله کمینه درجه گراف و مفاهیم مرتبط آن، فرمول بندی کنیم.