توزیع درجه

توزیع درجات گراف ابرپیوند ویکی‌پدیا (مقیاس لگاریتمی)

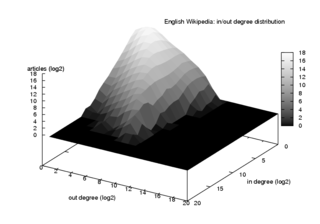
به تعداد اتصالات یک گره به گره‌های دیگر در حوزه مطالعاتی گراف و شبکه، درجه آن گره گویند. درجه توزیع، توزیع احتمال درجات گره‌ها در کل شبکه می‌باشد.

تعریف

درجه گره در یک شبکه (گاهی اوقات به اشتباه به عنوان همبندی) تعداد اتصالات یا لبه های یک گره به گره‌های دیگر است. اگر یک گراف جهت‌دار باشد به این معنی است لبه‌ها از یک گره به گره دیگر دارای جهت می‌باشند. در نتیجه هر گره دارای دو درجه متفاوت خواهد بود: درجه ورودی که تعداد لبه‌های ورودی آن گره و درجه خروجی تعداد لبه‌های خروجی آن گره می‌باشد.

به کسری از گره‌های یک شبکه با درجه k، درجه توزیع P(k).بنابراین اگر شبکه n گره داشته باشد و n_k تای آن‌ها درجه k داشته باشند, درجه توزیع P(k) = n_k/n خواهد بود.

به همین صورت می‌توان تعاریف دیگری را ارائه کرد. درجه توزیع تجمعی کسری از گره‌های با درجه کوچکتر از k و متمم درجه توزیع تجمعی کسری از گره‌ها با درجه بزرگتر یا مساوی باهای نودها که درجه همان اطلاعات نیز گاهی در قالب یک تجمعی درجه توزیعکسر از با درجه بزرگتر یا مساوی (k (1 - C;که در اینجا C درجه توزیع تجمعی می‌باشد،یعنی مکمل C).

توزیع درجات مشاهده شده

توزیع درجات در مطالعه هر دو شبکه‌های دنیای واقعی مانند اینترنت و شبکه‌های اجتماعی و شبکه‌های نظری بسیار مهم می‌باشد. ساده‌ترین مدل شبکه گراف تصادفی (برنولی) می‌باشد، که در آن هر یک از n گره با احتمال مستقل P( یا 1-p) وصل (یا غیروصل) هست. توزیع درجات k بسط دو جمله ای است:

$P(k)={n-1 \choose k}p^{k}(1-p)^{n-1-k},$

(و اگر n بسیار بزرگ باشد از توزیع پواسون خواهد داشت). اکثر شبکه‌ها در دنیای واقعی، توزیع درجات متفاوت با این مدل دارند. توزیع درجات دارای کشیدگی (چولگی) به سمت راست می‌باشد. به این معنی که تعداد زیادی از گره‌ها درجات کمی دارند و درجه پایین اما تعداد کمی از گره‌ها ، که هاب نامیده می‌شوند، درجات بالایی دارند.در بعضی از شبکه ها، برای مثال اینترنت، شبکه جهانی وب ، و بعضی از شبکه‌های اجتماعی توزیع درجهات به صورت تقریبی از قانون توان پیروی می‌کنند. در قانون توان توزیع درجات به صورت  P(k) ~ k^−γ می باشد که در آن γ ثابت است. چنین شبکه هایی، شبکه‌های مقیاس-مستقل(هر بخشی از شبکه ساختار مشابهی با کل شبکه دارد) نامیده می‌شوند.

جستارهای وابسته

• نظریه گراف
• شبکه‌های پیچیده
• شبکه‌های مقیاس مستقل
• گراف تصادفی
• ساختار قطع

منابع

• Albert, R.; Barabasi, A. -L. (2002). "Statistical mechanics of complex networks". Reviews of Modern Physics. 74: 47–97. arXiv:cond-mat/0106096. Bibcode:2002RvMP...74...47A. doi:10.1103/RevModPhys.74.47.
• Dorogovtsev, S.; Mendes, J. F. F. (2002). "Evolution of networks". Advances in Physics. 51 (4): 1079–1187. arXiv:cond-mat/0106144. Bibcode:2002AdPhy..51.1079D. doi:10.1080/00018730110112519.
• Newman, M. E. J. (2003). "The structure and function of complex networks". SIAM Review. 45 (2): 167–256. arXiv:cond-mat/0303516. Bibcode:2003SIAMR..45..167N. doi:10.1137/S003614450342480.
• Complex Networks: Structure, Robustness and Function. Cambridge University Press. 2010. Archived from the original on 4 اكتبر 2011. Retrieved 15 December 2016. {{cite book}}: Check date values in: |archive-date= (help)