چندضلعی ستارهای
| |||||||||
| نماد اشلفلی gcd(p,q)=۱ |
{p/q} | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| رأسها و اضلاع | p | ||||||||
| چگالی | q | ||||||||
| گروه تقارن | دوسطحی (Dp) | ||||||||
| چندضلعی همزاد | خودهمزاد | ||||||||
| اندازه زاویه داخلی (درجه) |
[۱] | ||||||||
یک چندضلعی ستارهای منظم، یک چندضلعی منتظم غیرمحدب است. در ریاضیات، تنها چندضلعیهای ستارهای منتظم مورد مطالعه قرار گرفتهاند و چندضلعیهای ستارهای عمومی (غیرمنتظم)، بهصورت رسمی تعریف نشدهاند.
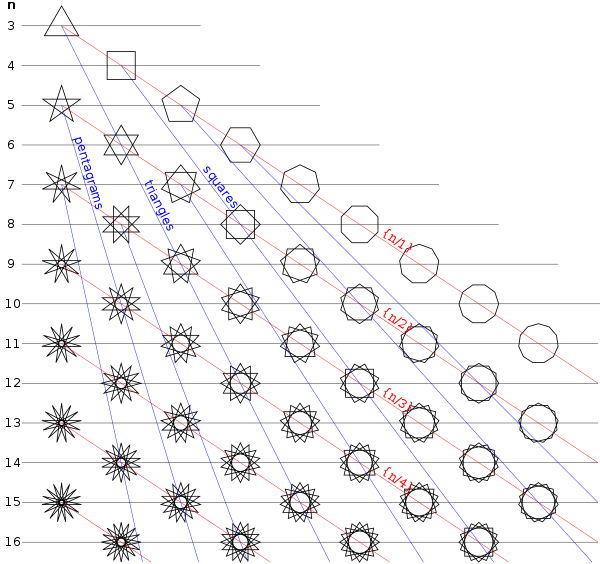
در هندسه، یک چندضلعی ستارهای منتظم، چندضلعی است که اضلاع آن یکدیگر را قطع میکنند، اندازه اضلاع و زوایای داخلی آن برابر بوده و با اتصال یک رأس یک چندضلعی p-وجهی منتظم ساده به یک رأس غیرمجاور و ادامهدادن این روند تا رسیدن دوباره به همان رأس ایجاد میشود.[۲] در یک چندضلعی ستارهای، هر ضلع آن تنها دو ضلع دیگر را قطع میکند. برای اعداد صحیح p و q، این چندضلعی میتواند با اتصال هر نقطهٔ qام از p نقطه که به فاصله یکسان بر روی یک دایره قرار گرفتهاند، ایجاد شود.[۳] نماد چنین چندضلعی {p/q} بوده که معادل {p/p-q} است. چندضلعیهای ستارهای منتظم زمانی ایجاد خواهند شد که p و q متباین باشند.
|
محیط و مساحت
[ویرایش]مساحت هر ستارۀ n پر منتظم، برابر با مجموع مساحت چندضلعی مولد آن و مساحت مثلث های اطراف آن است. به عنوان مثال، ستارۀ منتظم پنج پر زیر را در نظر بگیرید. مساحت ستاره در این حالت برابر است با:

برای تبدیل طول ضلع چندضلعی به طول ضلع مثلث (پر ستاره) می توانیم از قانون کسینوس ها استفاده کنیم:
با جایگذاری این عبارت در فرمول مساحت ستاره، خواهیم داشت:
با محاسبات جمع زوایای داخلی مثلث و زوایای داخلی چندضلعی می دانیم:
فلذا مقادیر سینوس و کسینوس گاما را می توان به شکل زیر ساده سازی کرد:
اگر این مقادیر را در فرمول مساحت ستاره قرار دهیم:
با گرفتن مخرج مشترک و ساده سازی عبارت داخل کروشه به فرمول زیر خواهیم رسید:
صورت کسر را می توانیم باز هم ساده تر کنیم تا به فرمول زیر برسیم:
این فرمول، فرمول محاسبۀ مساحت ستارۀ منتظم است که در آن a طول ضلع هر پر ستاره و n تعداد پرهای ستاره است.[۴]
پانویس
[ویرایش]- ↑ Kappraff, Jay (2002). Beyond measure: a guided tour through nature, myth, and number. World Scientific. p. 258. ISBN 978-981-02-4702-7.
- ↑ Coxeter, Harold Scott Macdonald (1973). Regular polytopes. Courier Dover Publications. ISBN 978-0-486-61480-9.
- ↑ Weisstein, Eric W. "Star Polygon". MathWorld.
- ↑ «بررسی هندسی شکل ستاره منتظم». رشد برهان ریاضی. ۲۷ (۱۰۶): ۱۰–۱۲. دی ۱۳۹۶.
















![{\displaystyle A_{star}={na^{2} \over 2}[{1+cos(4\pi /n) \over tan(\pi /n)}+sin(4\pi /n)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34847fbc538f4081bfa5ff4a7b2a8a082da67917)
![{\displaystyle A_{star}={na^{2} \over 2}[{cos(\pi /n)+cos(3\pi /n) \over sin(\pi /n)}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8a6fba1f8024745ec3fe3bc58a2188623163367)
![{\displaystyle A_{star}={na^{2} \over 2}[{2cos(2\pi /n) \over tan(\pi /n)}]={na^{2}cos(2\pi /n) \over tan(\pi /n)}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c48d016710c81e3b87c62971db4676770bc5cb3c)