پیش‌نویس:گروه متقارن آفین

گروه‌ متقارن آفین شاخه‌ای از جبر در ریاضیات است که به مطالعه و توصیف تقارن‌های محور اعداد و کاشی کاری مثلثی منظم صفحه و اجسام با ابعاد بالاتر مرتبط می‌پردازد. علاوه بر این توصیف هندسی، گروه‌های متقارن وابسته به روش دیگری نیز تعریف می‌شوند. مثلا:به عنوان مجموعه‌ای از جایگشت‌های (باز چینی) اعداد صحیح که در زمان خاصی به‌صورت متناوب هستند یا به اصطلاح تخصصی تر، به عنوان گروه با مولد و روابط (تعیین گروه با مولد و روابط بین آنها) است که در ترکیبیات و نظریهٔ نمایش بررسی می‌شوند. یک گروه متقارن محدود، شامل همه جایگشت‌های یک مجموعه متناهی است. هر گروه متقارن وابسته، توسیع گروهی از یک گروه متقارن محدود است. بسیاری از ویژگی‌های ترکیبی مهم گروه‌های متقارن محدود می‌تواند به گروه‌های متقارن وابسته متناظر تعمیم داده شود. آمار جایشگت (تصادفی) مانند جایگشت و وراونگی را می‌توان در وابسته تعریف کرد. همان‌طور که در حالت محدود، تعاریف ترکیبی طبیعی برای این آمار نیز تفسیر هندسی دارند. گروه‌های متقارن وابسته روابط نزدیکی با سایر موضوعات ریاضی دارند، از جمله الگو(ترفند)های شعبده‌بازی و گروه‌های بازتابی پیچیده خاص است. بسیاری از ویژگی‌های ترکیبی و هندسی آنها به خانواده گسترده‌تر گروه‌های کاکسیتر تعمیم داده می‌شود.

تعریف ها

گروه متقارن آفین را می‌توان توسط مولدها و روابط به عنوان گروهی مجرد، یا به طور معادل برحسب عبارات ملموس هندسی و مدل‌های ترکیبیاتی تعریف نمود.^[۱]

تعریف جبری

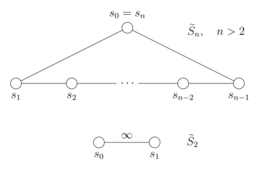
یکی از راه های تعریف گروه‌ها،استفاده از مولدها و روابط است. در این نوع تعریف، مولدها زیرمجموعه ای از عناصر گروه هستند که در صورت ترکیب، همه عناصر دیگر را تولید می کنند.روابط تعریف،سیستمی از معادلات هستند که مشخص می‌کنند چه زمانی ترکیب مولدها برابر هستند.^[الف]^[۲]به این ترتیب گروه متقارن وابسته ${\widetilde {S}}_{n}$ _ام،توسط یک مجموعه درست می‌شود.

$s_{0},s_{1},\ldots ,s_{n-1}$

از n_مین عنصر از رابطه زیر پیروی می‌کند: اگر $n\geq 3$ باشد

$s_{i}^{2}=1$ (که مولدها پیچشی هستند.)
$s_{i}s_{j}=s_{j}s_{i}$ اگر j متعلق به $j+1$ و $j-1$ نباشد،نشان می‌دهد برای این جفت ژنراتور خاصیت جابه‌جایی وجود دارد.
$s_{i}s_{i+1}s_{i}=s_{i+1}s_{i}s_{i+1}$

نکته مهم این است که در روابط فوق،اندازه‌ها هم‌نهشتn در نظر گرفته می‌شوند،در نتیجه رابطه شماره ۳ فقط در موارد خاص درست است $s_{0}s_{n-1}s_{0}=s_{n-1}s_{0}s_{n-1}$ (به روابط دوم و سوم روابط براید هم گفته می‌شود.^[۳]) اگر $n=2$ باشد،گروه متقارن آفین ${\widetilde {S}}_{2}$ ، یک گروه دووجهی بی نهایت است که توسط دو عنصر $s_{0},s_{1}$ تولید می‌شود و صرفا محدود به روابط $s_{0}^{2}=s_{1}^{2}=1$ است.^[۴]

این روابط را می‌توانند به شکل ویژه‌ای بازنویسی کرد که گروه‌های کاکسیتر تعریف می‌کند،بنابراین گروه‌های متقارن آفین همان گروه کاکسیتر هستند که در آن $s_{i}$ ها،مجموعه مولد کاکسیتر آنهاست.^[۴]هر گروه کاکسیتر ممکن است با گراف کاکسیتر-دینکین نشان داده شود که رئوس آن متناظر با مولدها باشد و یال‌ها روابط میان آنها را رمزگذاری می‌کند.^[۵]اگر $n\geq 3$ باشد،آنگاه نمودار کاکسیتر-دینکین برای ${\widetilde {S}}_{n}$ تبدیل به یک گراف $C_{n}$ می‌شود.(که در آن یال‌ها متناظر با روابط بین جفت مولدهای متوالی هستند و عدم وجود یک یال‌ بین جفت‌های مولدها،نشان می‌دهد که آنها قابل جابه‌جایی هستند.)

پانویس

↑ Shi (1986), p. 66.
↑ Gallian (2013), Chapter 26.
↑ Stembridge (1996), p. 355.
↑ ^۴٫۰ ^۴٫۱ Björner & Brenti (2005), pp. 5–6.
↑ Humphreys (1990), p. 31.

یادداشت‌ها

↑ اگر دقیق تر بخواهیم بگیم،تمامی روابط میان مولدها،می‌تواند توسط روابط داده شده توضیح داده شود،بنابراین آن گروه، بزرگترین گروه در بین گروه‌هایی است که مولدهای آنها روابط داده شده را برآورده می‌کند. این تعریف به صورت رسمی بر حسب نسبت گروه های آزاد داده شده است.

منابع

Allcock, Daniel (2002), "Braid pictures for Artin groups", Trans. Amer. Math. Soc., 354 (9): 3455–3474, doi:10.1090/S0002-9947-02-02944-6, S2CID 14473723
Beazley, Elizabeth; Nichols, Margaret; Park, Min Hae; Shi, XiaoLin; Youcis, Alexander (2015), "Bijective projections on parabolic quotients of affine Weyl groups", J. Algebr. Comb., 41 (4): 911–948, doi:10.1007/s10801-014-0559-9
Berg, Chris; Jones, Brant; Vazirani, Monica (2009), "A bijection on core partitions and a parabolic quotient of the affine symmetric group", J. Combin. Theory Ser. A, 116 (8): 1344–1360, arXiv:0804.1380, doi:10.1016/j.jcta.2009.03.013, S2CID 3032099
Billey, Sara C.; Jockusch, William; Stanley, Richard P. (1993), "Some Combinatorial Properties of Schubert Polynomials", J. Algebr. Comb., 2 (4): 345–374, doi:10.1023/A:1022419800503, S2CID 8628113
Björner, Anders; Brenti, Francesco (1996), "Affine permutations of type A", Electron. J. Combin., 3 (2): R18, doi:10.37236/1276, S2CID 2987208
Björner, Anders; Brenti, Francesco (2005), Combinatorics of Coxeter groups, Springer, doi:10.1007/3-540-27596-7, ISBN 978-3540-442387, S2CID 115235335
Cameron, Peter J. (1994), Combinatorics: Topics, Techniques, Algorithms, Cambridge University Press, doi:10.1017/CBO9780511803888, ISBN 978-0-521-45761-3, S2CID 115451799
Charney, Ruth; Peifer, David (2003), "The $K(\pi ,1)$ -conjecture for the affine briad groups", Comment. Math. Helv., 78 (3): 584–600, doi:10.1007/S00014-003-0764-Y, S2CID 54016405
Chmutov, Michael; Lewis, Joel Brewster; Pylyavskyy, Pavlo (2022), "An affine generalization of evacuation", Selecta Math., New Series, 28 (4): Paper 67, arXiv:1706.00471, doi:10.1007/s00029-022-00779-x, S2CID 119168718
Chmutov, Michael; Frieden, Gabriel; Kim, Dongkwan; Lewis, Joel Brewster; Yudovina, Elena (2022), "Monodromy in Kazhdan-Lusztig cells in affine type A", Math. Annalen, 386 (3–4): 1891–1949, arXiv:1806.07429, doi:10.1007/s00208-022-02434-4, S2CID 119669284
Chmutov, Michael; Pylyavskyy, Pavlo; Yudovina, Elena (2018), "Matrix-ball construction of affine Robinson-Schensted correspondence", Selecta Math., New Series, 24 (2): 667–750, arXiv:1511.05861, doi:10.1007/s00029-018-0402-6, S2CID 119086049
Clark, Eric; Ehrenborg, Richard (2011), "Excedances of affine permutations", Advances in Applied Mathematics, 46 (1–4): 175–191, doi:10.1016/j.aam.2009.12.006, S2CID 15349463
Coxeter, H.S.M. (1973), Regular Polytopes (3 ed.), Dover, ISBN 0-486-61480-8
Crites, Andrew (2010), "Enumerating pattern avoidance for affine permutations", Electron. J. Combin., 17 (1): R127, arXiv:1002.1933, doi:10.37236/399, S2CID 15383510
Ehrenborg, Richard; Readdy, Margaret (1996), "Juggling and applications to q-analogues", Discrete Math., 157 (1–3): 107–125, CiteSeerX 10.1.1.8.6684, doi:10.1016/S0012-365X(96)83010-X, S2CID 18149014
Eriksson, Henrik; Eriksson, Kimmo (1998), "Affine Weyl groups as infinite permutations", Electron. J. Combin., 5: R18, doi:10.37236/1356, S2CID 218962
Gallian, Joseph A. (2013), Contemporary Abstract Algebra (8th ed.), Brooks/Cole, ISBN 978-1-133-59970-8, LCCN 2012938179
Green, R.M. (2002), "On 321-Avoiding Permutations in Affine Weyl Groups", J. Algebr. Comb., 15 (3): 241–252, doi:10.1023/A:1015012524524, S2CID 10583938
Hanusa, Christopher R.H.; Jones, Brant C. (2010), "The enumeration of fully commutative affine permutations", Eur. J. Comb., 31 (5): 1342–1359, arXiv:0907.0709, doi:10.1016/j.ejc.2009.11.010, S2CID 789357
Hanusa, Christopher R.H.; Jones, Brant C. (2012), "Abacus models for parabolic quotients of affine Weyl groups", J. Algebra, 361: 134–162, arXiv:1105.5333v2, doi:10.1016/j.jalgebra.2012.03.029, S2CID 47583179
Humphreys, James E. (1990), Reflection groups and Coxeter groups, Cambridge University Press, doi:10.1017/CBO9780511623646, ISBN 0-521-37510-X, S2CID 121077209
Kac, Victor G. (1990), Infinite-dimensional Lie algebras (PDF) (3rd ed.), Cambridge University Press, doi:10.1017/CBO9780511626234, ISBN 0-521-46693-8
Kane, Richard (2001), Reflection groups and invariant theory, CMS Books in Mathematics/Ouvrages de Mathématiques de la SMC, Springer-Verlag, doi:10.1007/978-1-4757-3542-0, ISBN 0-387-98979-X, S2CID 119694827
Kent, IV, Richard P.; Peifer, David (2002), "A geometric and algebraic description of annular braid groups", International Conference on Geometric and Combinatorial Methods in Group Theory and Semigroup Theory (Lincoln, NE, 2000), Internat. J. Algebra Comput., 12 (1–2): 85–97, doi:10.1142/S0218196702000997, S2CID 13593688
Knutson, Allen; Lam, Thomas; Speyer, David E. (2013), "Positroid varieties: juggling and geometry", Compositio Mathematica, 149 (10): 1710–1752, doi:10.1112/S0010437X13007240, S2CID 16108179
Lam, Thomas (2015), "The shape of a random affine Weyl group element and random core partitions", Ann. Probab., 43 (4): 1643–1662, arXiv:1102.4405v3, doi:10.1214/14-AOP915, S2CID 119691692
Lapointe, Luc; Morse, Jennifer (2005), "Tableaux on $k+1$ -cores, reduced words for affine permutations, and $k$ -Schur expansions", J. Combin. Theory Ser. A, 112 (1): 44–81, doi:10.1016/j.jcta.2005.01.003, S2CID 161241
Lehrer, Gustav I.; Taylor, Donald E. (2009), Unitary reflection groups, Australian Mathematical Society Lecture Series, vol. 20, Cambridge University Press, ISBN 978-0-521-74989-3, MR 2542964
Lewis, Joel Brewster (2020), "A note on the Hurwitz action on reflection factorizations of Coxeter elements in complex reflection groups", Electron. J. Combin., 27 (2): P2.54, arXiv:2001.08238, doi:10.37236/9351, S2CID 219176795
Lewis, Joel Brewster; McCammond, Jon; Petersen, T. Kyle; Schwer, Petra (2019), "Computing reflection length in an affine Coxeter group", Trans. Amer. Math. Soc., 371 (6): 4097–4127, arXiv:1710.06920, doi:10.1090/tran/7472, S2CID 119617021
Lewis, Joel Brewster; Reiner, Victor (2016), "Circuits and Hurwitz action in finite root systems", The New York Journal of Mathematics, 22: 1457–1486, arXiv:1603.05969, MR 3603073, S2CID 1789116
Lusztig, George (1983), "Some examples of square integrable representations of semisimple p-adic groups", Trans. Amer. Math. Soc., 277: 623–653, doi:10.1090/S0002-9947-1983-0694380-4, S2CID 54190838
McCammond, Jon (2017), "The mysterious geometry of Artin groups", Winter Braids Lect. Notes, 4 (Winter Braids VII (Caen, 2017)): Exp. No. 1, 30, doi:10.5802/wbln.17, S2CID 128279613
McCammond, Jon; Sulway, Robert (2017), "Artin groups of Euclidean type", Invent. Math., 210 (1): 231–282, Bibcode:2017InMat.210..231M, doi:10.1007/s00222-017-0728-2, S2CID 253738806
Paolini, Giovanni; Salvetti, Mario (2021), "Proof of the $K(\pi ,1)$ conjecture for affine Artin groups", Invent. Math., 224 (2): 487–572, arXiv:1907.11795, doi:10.1007/s00222-020-01016-y, S2CID 253738279
Petersen, T. Kyle (2015), Eulerian Numbers, Birkhäuser Advanced Texts Basler Lehrbücher, Birkhauser, doi:10.1007/978-1-4939-3091-3, ISBN 978-1-4939-3090-6
Polster, Burkard (2003), The Mathematics of Juggling, Springer, doi:10.1007/b98883, ISBN 0-387-95513-5, S2CID 221274895
Reiner, Victor (1995), "The distribution of descents and length in a Coxeter group", Electron. J. Combin., 2: R25, doi:10.37236/1219, S2CID 6602595
Shephard, G. C.; Todd, J. A. (1954), "Finite unitary reflection groups", Canad. J. Math., 6: 274–304, doi:10.4153/CJM-1954-028-3, S2CID 3342221
Shi, Jian-Yi (1986), The Kazhdan-Lusztig Cells in Certain Affine Weyl Groups, Lecture Notes in Mathematics, vol. 1179, Springer, doi:10.1007/bfb0074968, ISBN 3-540-16439-1, S2CID 117899042
Shi, Jian Yi (1987), "Alcoves corresponding to an affine Weyl group", J. London Math. Soc., 2, 35 (1): 42–55, doi:10.1112/jlms/s2-35.1.42, S2CID 119897519
Shi, Jian-Yi (1991), "The generalized Robinson–Schensted algorithm on the affine Weyl group of type $A n -1$ ", J. Algebra, 139 (2): 364–394, CiteSeerX 10.1.1.551.3094, doi:10.1016/0021-8693(91)90300-W, S2CID 124324517
Shi, Jian-Yi (2002), "Certain imprimitive reflection groups and their generic versions", Trans. Amer. Math. Soc., 354 (5): 2115–2129, doi:10.1090/S0002-9947-02-02941-0, S2CID 53996908
Stembridge, John (1996), "On the Fully Commutative Elements of Coxeter Groups", J. Algebr. Comb., 5 (4): 353–385, doi:10.1007/BF00193185, S2CID 195239538
Viennot, G. (1977), "Une forme géométrique de la correspondance de Robinson-Schensted", in Foata, Dominique (ed.), Combinatoire et Représentation du Groupe Symétrique, Lecture Notes in Mathematics (به فرانسوی), vol. 579, Springer, pp. 29–58, doi:10.1007/BFb0090011, ISBN 978-3-540-08143-2, S2CID 118727388

[FOOTNOTEShi198666-1] Shi (1986), p. 66.

[FOOTNOTEGallian2013Chapter_26-3] Gallian (2013), Chapter 26.

[FOOTNOTEStembridge1996355-4] Stembridge (1996), p. 355.

[FOOTNOTEBjörnerBrenti20055–6-5] ۴٫۰ ^۴٫۱ Björner & Brenti (2005), pp. 5–6.

[FOOTNOTEHumphreys199031-6] Humphreys (1990), p. 31.

[2] اگر دقیق تر بخواهیم بگیم،تمامی روابط میان مولدها،می‌تواند توسط روابط داده شده توضیح داده شود،بنابراین آن گروه، بزرگترین گروه در بین گروه‌هایی است که مولدهای آنها روابط داده شده را برآورده می‌کند. این تعریف به صورت رسمی بر حسب نسبت گروه های آزاد داده شده است.

[۱]

[الف]

[۲]

[۳]

[۴]

[۵]