نظریه نرخ-اعوجاج

نظریه نرخ-اِعوِجاج (نرخِ اعوجاج خوانده نشود)، یک شاخه اصلی از نظریه اطلاعات است که اصول نظری برای فشرده سازیِ خطادارِ داده (دیتا) است. این نظریه سعی در حل مسئلهٔ مشخص کردن حداقل تعداد بیت برای هر سمبل دارد (که با نرخ R اندازه گرفته می‌شود) که باید در کانال انتقال یابد به گونه‌ای که منبع اولیه را بتوان به صورت تقریبی در مقصد بازیابی کرد، ضمن اینکه اعوجاج (Distortion) از حد معینی (D) بیشتر نشود.

مقدمه

نظریه نرخ-اعوجاج یک فرمول بندی ریاضی است که بیان می کند چه مقدار فشرده سازیِ خطا دار امکان‌پذیر است. بسیاری از روش‌های فشرده سازی، صدا، گفتار، تصویر ثابت یا متحرک، دارای تبدیلات، کوانتیزاسیون، و روندهایی برای تعیین نرخ بیت هستند که در قالب کلی توابع نرخ-اعوجاج قرار می گیرند.

نظریه نرخ-اعوجاج توسط شانون در کار اساسی اش در نظریه اطلاعات شکل گرفت.

در نظریه نرخ-اعوجاج، معمولاً نرخ به عنوان تعداد بیت مورد استفاده برای هر سمبل به منظور ارسال یا فشرده سازی شناخته می‌شود. در بسیاری از موارد ساده، اعوجاج به صورت متوسطِ (امیدِ ریاضی) مربع اختلاف سیگنال ورودی و خروجی تعریف می‌شود. اما، از آنجایی که تکنیک‌های فشرده سازی خطادار روی داده هایی اعمال می‌شوند که قرار است برای انسان قابل درک باشند (مانند موسیقی، تصاویر ثابت یا متحرک)، اندازه‌گیری اعوجاج باید به گونه‌ای مدل شود که متناسب با درک انسان باشد. بسیار شبیه استفاده از احتمالات در فشرده سازی خطا دار، معیارهای اعوجاج می‌توانند با توابع هزینه (همان گونه که در تخمین بِیزَین و تئوری تصمیم استفاده می‌شود)، بیان شوند. در فشرده سازی صوت، مدل‌های ادراکی (و در نتیجه اعوجاج ادراکی) نسبتاً خوب پیشرفت کرده‌اند و به صورت معمول در تکنیک‌های فشرده سازی نظیر MP3 یا Vorbis استفاده می‌شوند، اما اغلب ساده نیست که در غالب تئوری نرخ- اعوجاج آورده شوند. در فشرده سازی تصویر ثابت یا متحرک، مدل‌های مبتنی بر ادراک انسان کمتر توسعه یافته‌اند و به صورت محدود در ماتریس وزن‌های JPEG و MPEG استفاده می‌شود.

توابع نرخ-اعوجاج

توابعی که نرخ و اعوجاج را به هم مرتبط می‌کنند، جواب‌های مسئلهٔ کمینه سازی زیر هستند:

$\inf _{Q_{Y|X}(y|x)}I_{Q}(Y;X)\ {\mbox{subject to}}\ D_{Q}\leq D^{*}.$

در اینجا (Q_{Y | X}(y | x، که گاهی تست کانال نامیده می‌شود، تابع چگالی احتمال شرطی (PDF) خروجی کانال ارتباطی Y برای یک ورودی مفروض X است و (I_Q(Y ; X اطلاعات متقابل بین Y و X است که به صورت زیر تعریف می‌شود:

$I(Y;X)=H(Y)-H(Y|X)\,$

که (H(Y و (H(Y | X آنتروپی سیگنال خروجی (y) و آنتروپی شرطی سیگنال خروجی به شرط سیگنال ورودی است :

$H(Y)=-\int _{-\infty }^{\infty }P_{Y}(y)\log _{2}(P_{Y}(y))\,dy$

$H(Y|X)=-\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }Q_{Y|X}(y|x)P_{X}(x)\log _{2}(Q_{Y|X}(y|x))\,dx\,dy.$همچنین مسئله را می‌توان به صورت یک تابع نرخ-اعوجاج فرمول بندی کرد که قصد داریم آن را روی اعوجاج‌های دست یافتنی برای یک محدودیت روی نرخ مینیمم کنیم. عبارت مرتبط با آن به صورت خواهد بود:

$\inf _{Q_{Y|X}(y|x)}E[D_{Q}[X,Y]]\ {\mbox{subject to}}\ I_{Q}(Y;X)\leq R.$

این دو فرمول بندی به توابعی منجر می‌شود که معکوس یکدیگر هستند.

اطلاعات متقابل می‌تواند به عنوان معیاری باشد برای تفاوت عدم قطعیت گیرنده از سیگنال Y و عدم قطعیت از Y به شرط دانستن X. البته این کاهش عدم قطعیت به خاطر میزان اطلاعاتی است که بین فرستنده و گیرنده مخابره می‌شود. (I(Y; X

به عنوان مثال، اگر هیچ مخابره‌ای نداشته باشیم، آنگاه (H(Y |X) = H(Y و I(Y; X) = ۰. در طرف دیگر، اگر کانال مخابراتی بدون خطا باشد و سیگنال دریافتی Y برابر سیگنال ارسالی X باشد، آنگاه H(Y | X) = ۰ و (I(Y; X) = H(Y.

در تعریف نرخ- اعوجاج، اعوجاج بین X و Y برای یک(Q_{Y | X}(y | x هستند و حداکثر اعوجاج مجاز هستند. هنگامی که از میانگین مربع خطا به عنوان معیار اعوجاج استفاده می‌کنیم، داریم: (برای سیگنال‌های با دامنه پیوسته)

$D_{Q}=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }P_{X,Y}(x,y)(x-y)^{2}\,dx\,dy=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }Q_{Y|X}(y|x)P_{X}(x)(x-y)^{2}\,dx\,dy.$همان‌طور که معادله بالا نشان می‌دهد، محاسبهٔ یک تابع نرخ-اعوجاج نیاز به توصیف احتمالی ورودی X در قالب PDF آن دارد، و سپس به دنبال PDF شرطی ای (Q_{Y | X}(y | x می‌رود که نرخ را برای یک اعوجاج D^* کمینه کند.

یک تعریف آنالیزی برای حل این مسئلهٔ کمینه سازی، اغلب سخت بدست می‌آید، جز در مواردی که به دو مورد از آنها اشاره می‌کنیم. تابع نرخ-اعوجاج هر منبع از چند ویژگی اساسی پیروی می‌کند. مهم ترینشان این است که یک تابع پیوستهٔ اکیداً نزولی مقعر است.

اگر چه جواب آنالیتیکال برای این مسائل نادر است، حد بالا و پایینی نظیر حد پایین شانون (SLB) برای این توابع وجود دارد، که در مورد خطای مربع و منبع بی حافظه، عنوان می‌کند که برای هر منبع دلخواه با آنتروپی تفاضلی محدود داریم:

$R(D)\geq h(X)-h(D)\,$

که(h(D آنتروپی تفاضلی متغیر تصادفی گاوسی با واریانس D است. این حد پایین قابل تعمیم به منابع حافظه دار و سایر معیارهای اعوجاج است. یک ویژگی مهم SLB این است که در شرایط اعوجاج اندک برای گروه وسیعی از منابع باند سفتی در دسترس قرار می‌دهد.

الگوریتم Blahut–Arimoto یک روش مبتنی بر تکرار برای حل عددی تابع نرخ-اعوجاج برای الفبای محدود ورودی - خروجی منبع است و کارهای زیادی برای گسترش این راه حل به مسائل عمومی تری انجام شده است.

هنگام کار با منابع حافظه دار، ضروری است که تعریف تابع نرخ-اعوجاج بازنگری شود و به صورت یک حد روی دنباله‌هایی که طول افزایشی دارد دیده شود.

$R(D)=\lim _{n\rightarrow \infty }R_{n}(D)$

جایی که:

$R_{n}(D)={\frac {1}{n}}\inf _{Q_{Y^{n}|X^{n}}\in {\mathcal {Q}}}I(Y^{n},X^{n})$

و

${\mathcal {Q}}=\{Q_{Y^{n}|X^{n}}(Y^{n}|X^{n},X_{0}):E[d(X^{n},Y^{n})]\leq D\}$

که بالانویس‌ها یک دنباله کامل تا آن زمان را نشان میدهد و زیرنویس 0، حالت اولیه را نشان می‌دهد.

منبع گاوسی بی حافظه (مستقل)

اگر فرض کنیم که (P_X(x یک توزیع گاوسی با واریانس σ² و نمونه‌های آتی سیگنال X مستقل هستند (منبع بی حافظه است یا سیگنال‌ها ناهمبسته اند)، فرم بستهٔ زیر برای تابع نرخ-اعوجاج استخراج می‌شود:

$R(D)=\left\{{\begin{matrix}{\frac {1}{2}}\log _{2}(\sigma _{x}^{2}/D),&{\mbox{if }}0\leq D\leq \sigma _{x}^{2}\\\\0,&{\mbox{if }}D>\sigma _{x}^{2}.\end{matrix}}\right.$

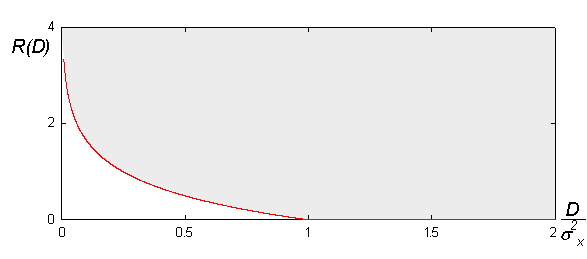
شکل زیر نشان می‌دهد که این تابع بدین صورت است:

نظریه نرخ-اعوجاج به ما می‌گوید هیچ سیستم فشرده سازی وجود ندارد که خارج از ناحیهٔ خاکستری عمل کند. خط قرمز یک باند برای فشرده سازهای عملی است. به عنوان یک قانون کلی این حد تنها با افزایش طول بلوک‌های کد امکان‌پذیر است. با این وجود، حتی در طول بلوک واحد امکان یافتن کوانتایز خوب به گونه‌ای که با فاصله خوبی از تابع نرخ-اعوجاج کار کند وجود دارد.

این تابع نرخ-اعوجاج تنها برای منابع گاوسی بدون حافظه برقرار است. منبع گاوسی سخت ترین منبع برای دیکد کردن است. برای یک خطای میانگین مربعات، این منبع به بیشترین تعداد بیت نیاز دارد. بهره‌وری یک سیستم فشرده سازی عملی که بر روی تصاویر کار می‌کند ممکن است به خوبی زیر باند پایین (R(D نشان داده شده باشد.

ارتباط نظریه نرخ-اعوجاج با ظرفیت کانال

فرض کنید می خواهیم اطلاعات منبعی را ارسال کنیم بطوری که اعوجاج از حد D تجاوز نکند. نظریه نرخ-اعوجاج می‌گوید که حداقل (R(D بیت برای هر سمپل از اطلاعات باید از منبع به گیرنده برسد. همچنان از نظریهٔ کدینگِ کانال شانون می‌دانیم که اگر آنتروپی منبع، H بیت برای هر سمبل باشد، و ظرفیت کانال (C (C<H باشد، آنگاه H-C بیت برای هر سمبل هنگام ارسال اطلاعات روی کانال از دست می‌رود. برای اینکه گیرنده بتواند اطلاعات را با حداکثر اعوجاج D بازیابی کند، باید از دست دادن اطلاعات در هنگام انتقال از بیشینه خطای قابل تحمل (H − R(D بیت برای هر سمیل بیشتر نباشد؛ که این به این معنی است که ظرفیت کانال باید حداقل بیشتر از (R(D باشد.

جستارهای وابسته

• Decorrelation
• بهینه‌سازی نرخ-اعوجاج
• کدگذاری منبع
• بسته‌بندی - کروی
• سفید کردن (نویز)
• Blahut-Arimoto الگوریتم

پیوند به بیرون

• PyRated: کد پایتون برای محاسبات ابتدایی در نظریه نرخ-اعوجاج است.
• VcDemo تصویر و ویدئو فشرده سازی ابزار یادگیری

<link rel="mw:PageProp/Category" href=". /رده:نظریه_اطلاعات"/>