قفل کشندی
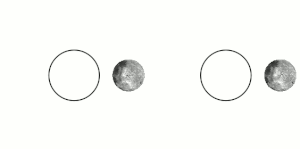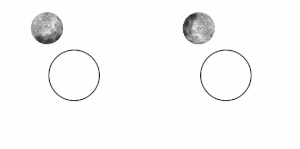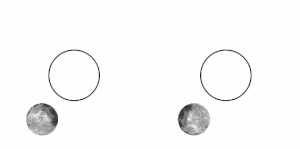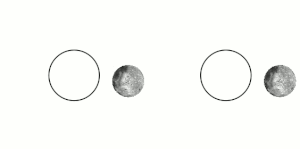
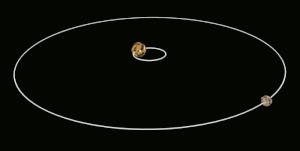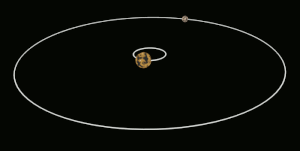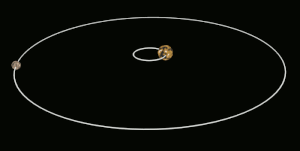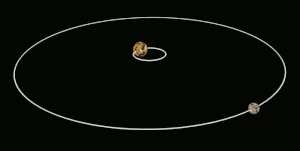
قفل کشندی (به انگلیسی: Tidal locking) یا قفل گرانشی (به انگلیسی: gravitational locking) زمانی پیش میآید که در اثر شیب نیروی کشندی، یک کره یا جرم آسمانی همیشه به سوی کره یا جرم آسمانی دیگری رو کرده باشد. آشناترین نمونهٔ این پدیده همبستگی جزر و مدی کنونی ماه نسبت به زمین است. چنین گردشی را گردش هماهنگ (به انگلیسی: synchronous rotation) میگویند. به بیان ساده تر پدیدهی قفل شدگی هنگامی روی میدهد که یک سیاره یا قمر به دلیل قرار گرفتن در فاصله نزدیک به منبع گرانشی خود – مانند سیاره بزرگتر یا ستاره مادر- چرخش وضعی و انتقالی کاملا مساوی پیدا می کندویک سمت سیاره یا قمر به سمت منبع گرانشی قفل میشود و طرف دیگر همیشه رو به فضا خواهد بود.
جرم آسمانی درگیر در این قفل برای هر بار گشتن به گرد محور خود ناچار به پیمودن یک دور کامل (در نمونهٔ نسبتی ۱ به ۱) گرداگرد سیاره یا جرم همتا دراین وابستگی است.
در منظومهٔ شمسی پدیدهٔ قفل جزر و مدی جریان نادری نیست. نشان داده شده که بسیاری از قمرهای مشتری، کیوان، اورانوس و نپتون هم در این وابستگی گرفتارند و گمان بر این است که بسیاری دیگر هم در رابطه با سیارهٔ مادر در شرایط قفل جزر و مدی باشند.
در آغاز بیشتر این جرم سبکتر است که گرفتار و ناچار به پیروی از جرم سنگینتر میشود. با گذشت زمان هر دو در این تنش به یکدیگر وابسته میشوند. نزدیکی بیشتر و تفاوت جرمی کمتر میان این دو، این زمان را کوتاهتر میکند و نیز؛ دوری بیشتر و تفاوت جرمی بالاتر، زمان کامل شدن این وابستگی را درازتر خواهد کرد.
اخترشناسان بر این باورند که ستارههای دوتایی نزدیک به هم نیز پدیدهٔ گردش هماهنگ را نسبت به یکدیگر تجربه میکنند.
قفل کشندی باعث میشود که در عطارد و زهره، طول روز از طول سال بیشتر باشد.[۱]
وقوع
[ویرایش]قمر زمین
[ویرایش]
چرخش ماه و تناوبهای مداری زمین به صورت جزر و مدی با یکدیگر قفل میشوند، بنابراین همیشه همان نیمکره ماه دیده میشود. سمت پنهان ماه نخستین بار در سال ۱۹۵۹ توسط کاوشگر لونا ۳ شوروی عکسبرداری شد.[۲]
وقتی زمین از ماه رصد میشود، به نظر نمیرسد که زمین در آسمان حرکت کند. در همان مکان باقی میماند در حالی که تقریباً تمام سطح خود را در حین چرخش بر محور خود نشان میدهد.[۳]
علیرغم اینکه دورههای چرخشی و مداری ماه دقیقاً قفل شدهاند، ممکن است حدود ۵۹ درصد از سطح ماه با مشاهدههای مکرر از زمین به دلیل پدیدههای رخگردی و اختلافمنظر مشاهده شود. رخگردی در درجه اول به دلیل تغییر سرعت مداری ماه به دلیل خروج از مرکز مدار آن ایجاد میشود: این اجازه میدهد تا حدود ۶ درجه بیشتر در امتداد محیط آن از زمین دیده شود. اختلاف منظر یک اثر هندسی است: در سطح زمین، ناظران از خطی که از طریق مراکز زمین و ماه میگذرد، منحرف میشوند، این حدود °۱ اختلاف در سطح ماه است که میتواند در اطراف ماه هنگام مقایسه مشاهدههای انجام شده در طول طلوع و غروب ماه دیده شود.[۴]در این وضعیت، یک نیمکره قمر همیشه در جهت گردش آن قرار دارد و نیمکره دیگر در خلاف جهت. اکثر قمرهای منظومه شمسی گردش رخ گرد دارند.کره ماه تنها جرم نجومی موجود در منظومه شمسی نیست که این اتفاق برایش می افتد. بلکه تمام اقمار بزرگ و اصلی سیاره های مشتری و زحل نیز همواره فقط یک روی خود را به مادرشان نشان می دهند
مقیاس زمانی
[ویرایش]با استفاده از فرمول زیر میتوان تخمینی از زمان قفل شدن یک جسم به صورت جزر و مدی بهدستآورد:[۵]
که:
- نرخ چرخش اولیه است که بر حسب رادیان بر ثانیه بیان میشود،
- نیمقطر بزرگ و نیمقطر کوچک حرکت قمر به دور سیاره است (با میانگین فاصله اوج و حضیض ارائه میشود)،
- گشتاور لختی قمر است که در آن جرم قمر است و شعاع متوسط قمر است،
- تابع اتلاف قمر است،
- ثابت گرانش است،
- جرم سیاره است (یعنی جسمی که به دور آن میچرخد) و
- عدد عشق جزر و مدی قمر است.
و بهطور کلی بسیار ضعیف شناخته شدهاند به جز ماه که دارد. برای یک تخمین تقریبی، معمولاً در نظر گرفته میشود (شاید محافظهکارانه، زمان قفل شدن بیش از حد تخمین زده شود)، و
که:
- چگالی قمر است
- گرانش سطحی قمر است
- سختی قمر است. این را میتوان تقریباً ۳×۱۰۱۰ N·m−۲ برای اجرام سنگی و ۴×۱۰۹ N·m−۲ برای اجسام یخی در نظر گرفت.
حتی دانستن اندازه و چگالی قمر پارامترهای زیادی را باقی میگذارد که باید تخمین زده شوند (به ویژه ω ,Q و μ)، به طوری که انتظار میرود هر زمان قفل محاسبهشده بهدستآمده، حتی تا فاکتورهای ده، نادرست باشد. علاوه بر این، در طول فاز قفل جزر و مد، محور نیمه اصلی ممکن است بهطور قابل توجهی با آنچه امروزه مشاهده میشود به دلیل شتاب جزر و مدی بعدی متفاوت باشد، و زمان قفل شدن به این مقدار بسیار حساس است.
از آنجایی که عدم قطعیت بسیار زیاد است، فرمولهای فوق را میتوان سادهتر کرد تا فرمول کمی دست و پاگیر به دست آورد. با فرض کروی بودن قمر، ، و حدس زدن یک دور در هر ۱۲ ساعت در حالت غیرقفلی اولیه معقول است (اکثر سیارکها دورههای چرخشی بین حدود ۲ ساعت تا حدود ۲ روز دارند)
با جرم بر حسب کیلوگرم، فواصل بر حسب متر و بر حسب نیوتن بر متر مربع. را میتوان تقریباً ۴×۱۰۱۰ N·m−۲ برای اجرام سنگی و ۴×۱۰۹ N·m−۲ برای اجسام یخی در نظر گرفت.
وابستگی بسیار شدیدی به محور نیمه اصلی وجود دارد .
برای قفل کردن یک جسم اولیه به قمر خود، مانند مورد پلوتون، پارامترهای قمر و بدنه اولیه را میتوان با هم عوض کرد.
یک نتیجه این است که با وجود برابری چیزهای دیگر (مانند و )، یک ماه بزرگ سریعتر از یک ماه کوچکتر در همان فاصله مداری از سیاره قفل میشود زیرا به اندازه مکعب شعاع قمر رشد میکند. نمونه احتمالی آن در منظومه زحل است، جایی که هایپریون به صورت جزر و مدی قفل نیست، در حالی که یاپتوس بزرگتر که در فاصله دورتری میچرخد، قفل است. با این حال، این واضح نیست زیرا هایپریون همچنین حرکت قوی از تیتان مجاور را تجربه میکند، که چرخش آن را مجبور به هرج و مرج میکند.
فرمولهای بالا برای مقیاس زمانی قفل ممکن است با دستورهای بزرگی خاموش باشند، زیرا وابستگی فرکانس را نادیده میگیرند. مهمتر از آن، آنها ممکن است برای باینریهای چسبناک (ستارههای دوتایی، یا سیارکهای دوتایی که قلوه سنگ هستند) قابل استفاده نباشند، زیرا دینامیک چرخش مدار چنین اجسامی عمدتاً با گرانروی آنها تعریف میشود، نه سفتی.[۷]
پلوتو و تاو گاوران
[ویرایش]نمونهٔ نادر این پدیده در منظومهٔ شمسی، گردش هماهنگ جرم فرانپتونی پلوتو سیارهٔ پیشین و یکی از بزرگترین اعضای شناخته شدهٔ کمربند کویپر امروز با ماه بزرگش شارون است. این دو به شکل دوجانبه رو در روی هم قفل جزر و مدی را تجربه میکنند.فضانوردان نام این واقعه را که به دلیل مبادلات و بر هم کنش های گرانشی و جاذبه ای میان اجرام مختلف نجومی رخ می دهد قفل یا انسداد گرانشی گذاشته اند
وارونهٔ این پدیده هم در بیرون از منظومهٔ شمسی دیده شده که میتواند نادر باشد. ستارهٔ تاو گاوران[۸] و سیارهٔ غول پیکرش در صورت فلکی گاوران[۹] در فاصلهٔ ۵۰ سال نوری از منظومهٔ شمسی جا دارند. این سیاره توانسته ستارهاش را در قفل جزر و مدی خود گرفتار و ناچار گرداند که همیشه رو در روی این سیاره - پیرو گردش هر ۳٫۳ روز آن سیاره باشد. این نخستین مورد در نوع خود بوده و با بهرهوری از گزینهٔ تلسکوپی نوسانات میکروسکوپی ستارگان یا تلسکوپ موست MOST به بودن و چگونگی رفتارش پی برده شدهاست.[۹]
منابع
[ویرایش]- ↑ published, Scott Dutfield (2022-04-28). "Why is a day on Venus longer than a year? The atmosphere may be to blame". Space.com (به انگلیسی). Archived from the original on 24 November 2023. Retrieved 2023-11-29.
- ↑ "Oct. 7, 1959 – Our First Look at the Far Side of the Moon". Universe Today. 2013-10-07. Archived from the original on 12 August 2022. Retrieved 2 December 2023.
- ↑ Cain, Fraser (2016-04-11). "When Will Earth Lock to the Moon?". Universe Today (به انگلیسی). Archived from the original on 28 May 2022. Retrieved 2020-08-03.
- ↑ Grego, Peter (2006). The Moon and How to Observe It. Springer London. pp. 47–50. ISBN 978-1-84628-243-0. Archived from the original on 21 October 2023. Retrieved 2 December 2023.
- ↑ B. Gladman; et al. (1996). "Synchronous Locking of Tidally Evolving Satellites". Icarus. 122 (1): 166–192. Bibcode:1996Icar..122..166G. doi:10.1006/icar.1996.0117. (See pages 169–170 of this article. Formula (9) is quoted here, which comes from S. J. Peale, Rotation histories of the natural satellites, in J. A. Burns, ed. (1977). Planetary Satellites. Tucson: University of Arizona Press. pp. 87–112.)
- ↑ Hanslmeier, Arnold (2018). Planetary Habitability And Stellar Activity. World Scientific Publishing Company. p. 99. ISBN 9789813237445. Archived from the original on 2023-10-04. Retrieved 2023-03-19.
- ↑ Efroimsky, M. (2015). "Tidal Evolution of Asteroidal Binaries. Ruled by Viscosity. Ignorant of Rigidity". The Astronomical Journal. 150 (4): 12. arXiv:1506.09157. Bibcode:2015AJ....150...98E. doi:10.1088/0004-6256/150/4/98. S2CID 119283628. 98.
- ↑ Walker, G. A. H. et al. (2008). "MOST detects variability on tau Bootis possibly induced by its planetary companion". Astronomy and Astrophysics 482 (2): 691–697. arXiv:0802.2732
- ↑ ۹٫۰ ۹٫۱ «SPACE.com - Role Reversal: Planet Controls a Star». بایگانیشده از اصلی در ۴ اوت ۲۰۰۸. دریافتشده در ۳ مارس ۲۰۱۵.
- مشارکتکنندگان ویکیپدیا. «Tidal locking». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۳۰ نوامبر ۲۰۲۳.

























