رایانش کوانتومی ابررسانا

رایانش کوانتومی ابررسانا (انگلیسی: Superconducting quantum computing) شاخه‌ای از فیزیک حالت جامد و رایانش کوانتومی است که مدار الکترونیکی با استفاده از ابررسانایی و کیوبیت‌های ابررسانا به‌عنوان اتم مصنوعی یا نقطه کوانتومی پیاده‌سازی می‌کند. برای کیوبیت‌های ابررسانا، دو حالت منطقی حالت پایه و حالت برانگیخته هستند که به‌ترتیب با $|g\rangle {\text{ و }}|e\rangle$ نشان داده می‌شوند.

پژوهش در زمینه رایانش کوانتومی ابررسانا توسط شرکت‌هایی نظیر گوگل، آی‌بی‌ام، آیمک، ریتیون بی‌بی‌ان تکنالوجیز، Rigetti, و اینتل انجام می‌شود. بسیاری از پردازنده‌های کوانتومی (QPUs) که اخیراً توسعه یافته‌اند، از معماری ابررسانا استفاده می‌کنند. تا تاریخ تا تاریخ مه ۲۰۱۶، تا ۹ کیوبیت کاملاً قابل کنترل در برنامه‌نویسی آرایه‌ای یک‌بعدی و تا ۱۶ کیوبیت در معماری دوبعدی نشان داده شده است.

در اکتبر ۲۰۱۹، گروه Martinis که با گوگل همکاری داشتند، مقاله‌ای منتشر کردند که در آن برتری کوانتومی نوینی با استفاده از تراشه‌ای متشکل از ۵۳ کیوبیت ابررسانا به نمایش گذاشته شد.

پیش‌زمینه

مدل‌های کلاسیک محاسبات بر پیاده‌سازی‌های فیزیکی سازگار با قوانین مکانیک کلاسیک استوارند. توصیفات کلاسیک تنها برای سیستم‌هایی که شامل تعداد نسبتاً زیادی اتم هستند، دقیق عمل می‌کنند. توصیف جامع‌تر طبیعت از طریق مکانیک کوانتومی ارائه می‌شود. رایانش کوانتومی پدیده‌های کوانتومی را در کاربردهایی فراتر از تقریب‌های کلاسیک با هدف پردازش و ارتباط اطلاعات کوانتومی بررسی می‌کند. مدل‌های مختلفی برای رایانش کوانتومی وجود دارند، اما محبوب‌ترین مدل‌ها از مفاهیم کیوبیت‌ها و دروازه‌های منطقی کوانتومی (یا رایانش کوانتومی مبتنی بر دروازه‌های منطقی ابررسانا) بهره می‌گیرند.

ابررساناها به این دلیل استفاده می‌شوند که در دماهای پایین رسانایی بی‌نهایت و مقاومت صفر دارند. هر کیوبیت با استفاده از مدارهای نیمه‌رسانا که شامل مدار ال‌سی (یک خازن و یک القاگر) است، ساخته می‌شود. خازن‌ها و القاگرهای ابررسانا برای ایجاد مداری تشدیدی به کار می‌روند که تقریباً هیچ انرژی‌ای به صورت گرما تلف نمی‌کند، زیرا گرما می‌تواند اطلاعات کوانتومی را مختل کند. این مدارهای تشدیدی ابررسانا به‌عنوان اتم‌های مصنوعی شناخته می‌شوند که می‌توانند به‌عنوان کیوبیت‌ها استفاده شوند. پیاده‌سازی نظری و فیزیکی مدارهای کوانتومی تفاوت‌های زیادی دارند. پیاده‌سازی مدار کوانتومی مجموعه‌ای از چالش‌های خاص خود را دارد و باید از معیارهای دی‌وینچنزو پیروی کند. این معیارها توسط دیوید پی دی‌وینچنزو، فیزیک‌دان نظری، پیشنهاد شده‌اند. این معیارها شامل پنج شرط اولیه برای اطمینان از سازگاری رایانه کوانتومی با اصول مکانیک کوانتومی و دو شرط دیگر برای انتقال اطلاعات در شبکه است.

ما حالت‌های پایه و برانگیخته این اتم‌ها را به ترتیب به حالت‌های ۰ و ۱ نگاشت می‌کنیم، زیرا این مقادیر انرژی گسسته و متمایز هستند و با اصول مکانیک کوانتومی سازگارند. با این حال، در چنین ساختاری، یک الکترون می‌تواند به چندین حالت انرژی دیگر جهش کند و محدود به حالت برانگیخته مورد نظر ما نباشد؛ بنابراین ضروری است که سیستم تنها تحت تأثیر فوتون‌هایی قرار گیرد که اختلاف انرژی لازم برای جهش از حالت پایه به حالت برانگیخته را دارند. با این حال، این موضوع یک مشکل اساسی باقی می‌گذارد؛ ما به فواصل نابرابر بین سطوح انرژی نیاز داریم تا از انتقالات بین جفت‌های همسایه حالت‌ها توسط فوتون‌های با انرژی یکسان جلوگیری شود. تقاطع‌های جوزفسون عناصر ابررسانایی با القای غیرخطی هستند که برای پیاده‌سازی کیوبیت‌ها بسیار مهم‌اند. استفاده از این عنصر غیرخطی در مدار تشدیدی ابررسانا باعث ایجاد فواصل نابرابر بین سطوح انرژی می‌شود.

کیوبیت‌ها

مقالهٔ اصلی: کیوبیت

یک کیوبیت تعمیمی از بیت (سیستمی با دو حالت کوانتومی) است که قادر به اشغال برهم‌نهی کوانتومی از هر دو حالت می‌باشد. در مقابل، یک دروازه کوانتومی تعمیمی از دروازه منطقی است که ماتریس تبدیل یک یا چند کیوبیت را پس از اعمال دروازه با توجه به حالت اولیه‌شان توصیف می‌کند. پیاده‌سازی فیزیکی کیوبیت‌ها و دروازه‌ها به همان دلایلی چالش‌برانگیز است که مشاهده پدیده‌های کوانتومی در زندگی روزمره دشوار است؛ زیرا این پدیده‌ها در مقیاس‌های بسیار کوچک رخ می‌دهند. یکی از روش‌های دستیابی به رایانه‌های کوانتومی، پیاده‌سازی ابررسانایی است که اثرات کوانتومی را در مقیاس ماکروسکوپی قابل مشاهده می‌کند، هرچند به بهای دماهای عملیاتی بسیار پایین.

ابررساناها

مقالهٔ اصلی: ابررسانایی

برخلاف رساناهای معمولی، ابررساناها دارای یک نقطه بحرانی هستند که در آن مقاومت تقریباً به صفر می‌رسد و رسانایی به‌طور قابل توجهی افزایش می‌یابد. در ابررساناها، حامل‌های بار اصلی جفت‌های الکترونی (که به نام جفت کوپر شناخته می‌شوند) هستند، نه فرمیون‌های منفرد که در رساناهای معمولی یافت می‌شوند. جفت‌های کوپر به صورت آزاد به هم پیوند دارند و دارای یک حالت انرژی پایین‌تر از انرژی فرمی هستند. الکترون‌های تشکیل‌دهنده جفت کوپر دارای اندازه حرکت و اسپین برابر و مخالف هستند، به طوری که اسپین کلی جفت کوپر یک عدد صحیح است. ازاین‌رو، جفت‌های کوپر بوزون هستند. دو ابررسانای پرکاربرد در مدل‌های کیوبیت ابررسانا، نیوبیم و تانتالم هستند که هر دو ابررسانای باند-d محسوب می‌شوند.

چگالش بوز–اینشتین

مقالهٔ اصلی: چگالش بوز–اینشتین

زمانی که مجموعه‌ای از بوزون‌ها تا نزدیکی صفر مطلق سرد شوند، در پایین‌ترین سطح انرژی کوانتومی خود (یعنی حالت پایه) فرومی‌ریزند و حالتی از ماده را تشکیل می‌دهند که به چگالش بوز–اینشتین معروف است. برخلاف فرمیون‌ها، بوزون‌ها می‌توانند در یک سطح انرژی کوانتومی (یا حالت کوانتومی) قرار گیرند و از اصل طرد پاولی پیروی نمی‌کنند. به‌طور کلاسیک، چگالش بوز–اینشتین را می‌توان به‌عنوان مجموعه‌ای از ذرات که در یک مکان یکسان در فضا قرار گرفته‌اند و تکانه برابری دارند تصور کرد. ازآنجاکه نیروهای تعاملی بین بوزون‌ها به حداقل می‌رسد، چگالش بوز–اینشتین به‌طور مؤثر به‌عنوان یک ابررسانا عمل می‌کند. به همین دلیل، ابررساناها در محاسبات کوانتومی استفاده می‌شوند، زیرا دارای رسانایی تقریباً بی‌نهایت و مقاومت نزدیک به صفر هستند. مزایای ابررسانا نسبت به رسانای معمولی دوگانه است: از یک سو، ابررساناها می‌توانند به‌صورت نظری سیگنال‌ها را تقریباً به‌صورت آنی انتقال دهند و از سوی دیگر، بدون اتلاف انرژی به‌طور نامحدود کار کنند. چشم‌انداز تحقق رایانه‌های کوانتومی ابررسانا با توجه به توسعه اخیر ناسا در آزمایشگاه اتم سرد در فضا، امیدوارکننده‌تر می‌شود. در این محیط، چگالش‌های بوز–اینشتین به‌راحتی به دست می‌آیند و برای مدت‌زمان طولانی‌تر (بدون اتلاف سریع) در غیاب محدودیت‌های گرانش پایدار می‌مانند.

مدارهای الکتریکی

در هر نقطه از یک مدار الکتریکی ابررسانا (یک شبکه از عنصر الکتریکیها)، تابع موج چگالش که توصیف‌کننده جریان بار الکتریکی است، با استفاده از عدد مختلط و دامنه احتمال تعریف می‌شود. در مدارهای الکتریکی رساناهای معمولی، همین توصیف برای حامل بارهای منفرد صادق است، اما در تحلیل ماکروسکوپی، توابع موج مختلف به‌طور میانگین محاسبه می‌شوند و مشاهده اثرات کوانتومی غیرممکن می‌شود. بااین‌حال، تابع موج چگالش در طراحی و اندازه‌گیری اثرات کوانتومی ماکروسکوپی مفید است. مشابه تراز انرژیهای گسسته اتمی در مدل بور، تنها تعداد مشخصی از کوانتوم شار مغناطیسی می‌تواند به یک حلقه ابررسانا نفوذ کند. در هر دو مورد، کوانتش ناشی از دامنه پیچیده یک تابع پیوسته است. برخلاف پیاده‌سازی‌های میکروسکوپی رایانه‌های کوانتومی (مانند اتم‌ها یا فوتون‌ها)، پارامترهای مدارهای ابررسانا با تنظیم مقادیر (کلاسیک) عناصر الکتریکی تشکیل‌دهنده آن‌ها طراحی می‌شوند، برای مثال با تغییر ظرفیت خازنی یا ضریب خودالقایی.

برای به‌دست آوردن یک توصیف مکانیکی کوانتومی از یک مدار الکتریکی، چندین گام لازم است:

1. تمام عناصر الکتریکی باید به‌جای جریان الکتریکی و ولتاژ ماکروسکوپی مورد استفاده در مدارهای کلاسیک، با دامنه و فاز تابع موج چگالش توصیف شوند. برای مثال، مربع دامنه تابع موج در هر نقطه دلخواه در فضا احتمال یافتن یک حامل بار در آن نقطه را نشان می‌دهد؛ بنابراین، مربع دامنه معادل توزیع بار کلاسیک است.
2. شرط دوم این است که قانون‌های مداری کیرشهف به‌طور تعمیم‌یافته در هر گره از شبکه مدار اعمال شوند تا معادله حرکت سیستم به دست آید.
3. در نهایت، این معادلات حرکت باید به مکانیک لاگرانژی بازنویسی شوند تا یک هامیلتونین به‌دست آید که انرژی کل سیستم را توصیف کند.

فناوری

ساخت و تولید

دستگاه‌های محاسبات کوانتومی ابررسانا معمولاً در مهندسی فرکانس رادیویی طراحی می‌شوند، در یخچال‌هایی رقیق‌سازی با دمای کمتر از ۱۵ کلوین خنک می‌شوند و با استفاده از ابزارهای الکترونیکی رایج مانند سنتزکننده فرکانس و تحلیل‌گر طیف کنترل می‌شوند. ابعاد معمول این دستگاه‌ها در محدوده میکرومتر قرار دارد، با دقت زیر میکرومتر، که امکان طراحی راحت یک سیستم هامیلتونین (مکانیک کوانتومی) را با استفاده از فناوری آی‌سی (مدارهای مجتمع) فراهم می‌کند.

تولید کیوبیت‌های ابررسانا شامل فرآیندهایی از جمله چاپ سنگی، رسوب‌گذاری فلز، چاپ فلزی و اکسایش-کاهش کنترل‌شده است، همان‌طور که در مرجع توضیح داده شده است.

تولیدکنندگان به بهبود عمر کیوبیت‌های ابررسانا ادامه می‌دهند و از اوایل دهه ۲۰۰۰ پیشرفت‌های قابل‌توجهی داشته‌اند.

پیوند جوزفسون

یک پیوند جوزفسون که در آن C یک لایه نازک از عایق است و A و B جریان‌های (ابررسانا) با توابع موج متفاوت هستند

یکی از ویژگی‌های متمایز مدارهای کوانتومی ابررسانا، استفاده از اثر جوزفسون است. پیوندهای جوزفسون یک عنصر الکتریکی هستند که در ابررسانایی وجود ندارند. به یاد داشته باشید که پیوند الکتریکی یک اتصال ضعیف بین دو رسانا (در اینجا یک رسانای ابررسانا) در دو طرف یک لایه نازک از ماده عایق الکتریکی است که تنها چند اتم ضخامت دارد و معمولاً با استفاده از روش فن نیمایر-دولان ساخته می‌شود.

دستگاه پیوند جوزفسون حاصل، اثر جوزفسون را نشان می‌دهد که در آن پیوند یک ابرجریان تولید می‌کند. تصویر یک پیوند جوزفسون منفرد در سمت راست نمایش داده شده است. تابع موج چگال در دو طرف پیوند به‌طور ضعیفی همبستگی دارند، به این معنی که آنها می‌توانند فازهای ابررسانای متفاوتی داشته باشند. این تمایز در خطسانی با یک سیم ابررسانای پیوسته تفاوت دارد، زیرا در یک سیم ابررسانای پیوسته تابع موج در سراسر پیوند باید تابع پیوسته باشد.

جریان از طریق پیوند به‌وسیله تونل‌زنی کوانتومی جریان پیدا می‌کند، به‌طوری‌که به نظر می‌رسد به صورت لحظه‌ای از یک طرف پیوند به طرف دیگر «تونل می‌زند». این پدیده تونل‌زنی تنها در سیستم‌های کوانتومی مشاهده می‌شود. به این ترتیب، تونل‌زنی کوانتومی برای ایجاد القای غیرخطی استفاده می‌شود، که برای طراحی کیوبیت ضروری است زیرا امکان طراحی ناهماهنگی را فراهم می‌کند که در آن سطوح انرژی به صورت مجزا (یا کوانتیزه) با فاصله‌های نامساوی بین سطوح انرژی، که با $\Delta E$ نشان داده می‌شود، تفکیک می‌شوند.

در مقابل، نوسانگر هماهنگ کوانتمی نمی‌تواند به عنوان کیوبیت استفاده شود، زیرا هیچ راهی برای انتخاب تنها دو حالت از آن وجود ندارد؛ چراکه فاصله بین هر سطح انرژی و سطح بعدی دقیقاً یکسان است.

انواع کیوبیت

سه نوع اصلی کیوبیت ابررسانا عبارت‌اند از کیوبیت فاز، کیوبیت بار و کیوبیت شار. بسیاری از ترکیبات این انواع اصلی نیز وجود دارند که شامل فلکسونیوم، ترانسمون، ایکسمون، و کوانتونیوم.

در هر پیاده‌سازی کیوبیت، حالت کوانتومی منطقی $\{|0\rangle ,|1\rangle \}$ به حالت‌های مختلف سیستم فیزیکی نگاشت می‌شود (معمولاً به تراز انرژیهای مجزا یا برهم‌نهی کوانتومی آنها). هر یک از سه نوع اصلی نسبت‌های متفاوتی از انرژی جوزفسون به انرژی شارژ دارند. انرژی جوزفسون به انرژی ذخیره‌شده در پیوندهای جوزفسون هنگام عبور جریان اشاره دارد و انرژی شارژ انرژی موردنیاز برای بارگذاری یک جفت کوپر به ظرفیت کل پیوند است.

انرژی جوزفسون به صورت زیر نوشته می‌شود:

نمودار انواع کیوبیت ابررسانا بر اساس نسبت انرژی جوزفسون به انرژی شارژ با یک راهنما در سمت راست. بالای سمت چپ مدار الکتریکی یونیمون را نشان می‌دهد.

$U_{j}=-{\frac {I_{0}\Phi _{0}}{2\pi }}\cos \delta$,

که در آن $I_{0}$ جریان بحرانی پیوند جوزفسون، $\textstyle \Phi _{0}={\frac {h}{2e}}$ کوانتوم شار مغناطیسی (ابررسانا)، و $\delta$ فاز (موج) پیوند است.

توجه داشته باشید که عبارت $cos\delta$ نشان‌دهنده غیرخطی بودن پیوند جوزفسون است. انرژی شارژ نیز به صورت زیر نوشته می‌شود:

$E_{C}={\frac {e^{2}}{2C}}$,

که در آن $C$ ظرفیت پیوند و $e$ بار الکترون است.

از بین سه نوع اصلی، کیوبیت‌های فاز بیشترین تعداد جفت کوپر را برای تونل زدن از طریق پیوند امکان‌پذیر می‌کنند، سپس کیوبیت‌های شار، و کیوبیت‌های بار کمترین تعداد را اجازه می‌دهند.

کیوبیت فاز

کیوبیت فاز (Phase Qubit) دارای نسبت انرژی جوزفسون به انرژی بار در مرتبه بزرگی $10^{6}$ است. برای کیوبیت‌های فاز، ترازهای انرژی به نوسانات مختلف بار کوانتومی در یک اتصال جوزفسون مربوط می‌شوند، جایی که بار و فاز به ترتیب مشابه با تکانه و مکان در یک نوسانگر هماهنگ کوانتمی هستند. لازم است ذکر شود که در این زمینه، فاز به عنوان آرگومان مختلط تابع موج ابررسانا (که به آن گذار فاز ابررسانا نیز گفته می‌شود) در نظر گرفته می‌شود، نه فاز میان حالت‌های مختلف کیوبیت.

تصویر سمت چپ یک حلقه ابررسانا از نوع فلوکسونیوم را نشان می‌دهد که از مجموعه‌ای از اتصالات جوزفسون با مساحت‌های بزرگ‌تر و یک اتصال جوزفسون با مساحت کوچک‌تر تشکیل شده است، همان‌طور که توسط میکروسکوپ الکترونی نشان داده شده است. تصویر بالا سمت راست اجزای مدار فلوکسونیوم را نمایش می‌دهد، و تصویر پایین سمت راست اتصال جوزفسون با مساحت کوچک‌تر را نشان می‌دهد.

کیوبیت فلوکس

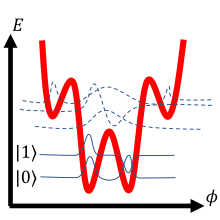
کیوبیت فلوکس (Flux Qubit) (که به آن کیوبیت جریان پایدار نیز گفته می‌شود) دارای نسبت انرژی جوزفسون به انرژی بار در مرتبه بزرگی $10$ است. برای کیوبیت‌های فلوکس، ترازهای انرژی به تعداد مختلفی از کوانتوم‌های فلکس مغناطیسی که در یک حلقه ابررسانا به دام افتاده‌اند مربوط می‌شوند.

فلوکسونیوم

کیوبیت‌های فلوکسونیوم(Fluxonium) یک نوع خاص از کیوبیت‌های فلوکس هستند که در آن اتصال جوزفسون با یک القاگر خطی $E_{J}\gg E_{L}$ where $E_{L}=(\hbar /2e)^{2}/L$) است. در عمل، القاگر خطی معمولاً با آرایه‌ای از اتصالات جوزفسون پیاده‌سازی می‌شود که از تعداد زیادی (که معمولاً $N>100$) اتصال جوزفسون بزرگ‌شده که به صورت سری به هم متصل شده‌اند، تشکیل شده است. تحت این شرایط، هامیلتونیان فلوکسونیوم به صورت زیر نوشته می‌شود:

${\hat {H}}=4E_{C}{\hat {n}}^{2}+{\frac {1}{2}}E_{L}({\hat {\phi }}-\phi _{\mathrm {ext} })^{2}-E_{J}\cos {\hat {\phi }}$.

یکی از ویژگی‌های مهم کیوبیت فلوکسونیوم، همدوسی طولانی‌تر در نقطه شیرین نصف فلکس است که می‌تواند بیش از ۱ میلی‌ثانیه باشد. یکی دیگر از مزایای مهم کیوبیت فلوکسونیوم که در نقطه شیرین قرار دارد، آن‌است که دارای غیرهارمونیکی بزرگ است، که به کنترل سریع محلی با مایکروویو و کاهش مشکلات ازدحام طیفی کمک می‌کند و منجر به مقیاس‌پذیری بهتر می‌شود.

کیوبیت بار

کیوبیت بار (Charge qubit)، که همچنین با نام جعبه جفت کوپر شناخته می‌شود، دارای نسبت انرژی جوزفسون به انرژی بار در حدود $<1$ است. برای کیوبیت‌های بار، سطوح انرژی مختلف به تعداد صحیحی از جفت کوپرها در یک جزیره ابررسانا (منطقه کوچک ابررسانا با تعداد کنترل‌شده حامل‌های بار) مربوط می‌شوند. در واقع، اولین کیوبیت تجربی، جعبه جفت کوپر بود که در سال ۱۹۹۹ به دست آمد.

دستگاهی شامل چهار کیوبیت ابررسانای ترنس‌مون، چهار اتوبوس کوانتومی و چهار تشدیدگر که توسط آی‌بی‌ام ساخته شده و در ژورنال npj Quantum Information در ژانویه ۲۰۱۷ منتشر شده است.

ترنس‌مون

ترنس‌مون‌ها (Transmon) نوع خاصی از کیوبیت‌ها هستند که دارای خازن شنت به‌طور خاص طراحی‌شده برای کاهش نویز هستند. مدل کیوبیت ترنس‌مون بر اساس جعبه جفت کوپر طراحی شده است. (که در جدول بالا در ردیف اول ستون اول نشان داده شده است). همچنین، ترنس‌مون اولین کیوبیتی بود که برتری کوانتومی را نشان داد. افزایش نسبت انرژی جوزفسون به انرژی بار موجب کاهش نویز می‌شود. دو ترنس‌مون می‌توانند با استفاده از تزویج خازنی به هم متصل شوند. برای این سیستم ۲-کیوبیتی، هامیلتونی به صورت زیر نوشته می‌شود:

${\hat {H}}={\frac {\hbar J}{2}}(\sigma _{1}^{x}\sigma _{2}^{x}+\sigma _{1}^{y}\sigma _{2}^{y})$,

که در آن $J$ چگالی جریان الکتریکی و $\sigma$ چگالی بار الکتریکی است.

ایکس‌مون

ایکس‌مون (Xmon) شباهت زیادی به ترنس‌مون دارد و بر اساس مدل ترنس‌مون سطح‌پانک طراحی شده است. ایکس‌مون در واقع یک ترنس‌مون قابل تنظیم است. تفاوت اصلی بین کیوبیت‌های ترنس‌مون و ایکس‌مون این است که کیوبیت‌های ایکس‌مون با یکی از پدهای خازنی خود به زمین متصل شده‌اند.

گاتمون

نوع دیگری از کیوبیت ترنس‌مون، گاتمون (Gatemon) است. مانند ایکس‌مون، گاتمون نیز یک تغییرپذیر از ترنس‌مون است. گاتمون از طریق ولتاژ آستانه قابل تنظیم است.

مدار ابررسانا شامل ۳ یونیمون (آبی)، که هر کدام به تشدیدگرها (قرمز)، خطوط درایو (سبز) و خطوط پروب مشترک (زرد) متصل هستند.

یونیمون

در سال ۲۰۲۲، محققان از IQM Quantum Computers، دانشگاه آلتو و VTT Technical Research Centre فنلاند یک کیوبیت ابررسانای جدید به نام یونیمون (Unimon) کشف کردند. یونیمون یک کیوبیت نسبتاً ساده است که از یک اتصال جوزفسون واحد تشکیل شده که توسط یک القاگر خطی (با اندوکتانس که به جریان بستگی ندارد) داخل یک تشدیدگر (ابررسانا) شانت شده است. کیوبیت‌های یونیمون دارای ناهماهنگی بیشتر هستند و زمان عملکرد سریع‌تری را نشان می‌دهند که منجر به کاهش حساسیت به خطاهای نویزی می‌شود. علاوه بر ناهماهنگی بیشتر، مزایای دیگر کیوبیت یونیمون شامل کاهش حساسیت به نویز شار و عدم حساسیت کامل به نویز بار DC است.

آرکیتایپ‌های کیوبیت ابررسانا

نوع بعد	شارژ کیوبیت	کیوبیت RF-SQUID (نمونه اولیه Flux Qubit)	کیوبیت فاز
مدار	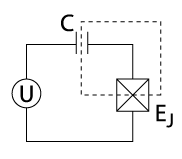مدار کیوبیت بار. یک جزیره ابررسانا (که با یک خط چین احاطه شده) بین اتصالات یک خازن با ظرفیت خازنی $C$ و یک اثر جوزفسون با انرژی $E_{J}$ که با ولتاژ $U$ بایاس شده است، تعریف می‌شود.	مدار کیوبیت فلکس. یک حلقه ابررسانا با ضریب خودالقایی $L$ که توسط یک تقاطع با انرژی جوزفسون $E_{J}$ قطع شده است. شار مغناطیسی $\Phi$ توسط یک خط فلکس با جریان الکتریکی $I_{0}$ بایاس می‌شود.	مدار کیوبیت فاز. یک اتصال جوزفسون با پارامتر انرژی $E_{J}$ که توسط جریان $I_{0}$ بایاس می‌شود.
هامیلتونی (مکانیک کوانتومی)	$H=E_{C}(N-N_{g})^{2}-E_{J}\cos \phi$ در اینجا $N$ تعداد جفت کوپر برای تونل‌زنی کوانتومی از طریق تقاطع است، $N_{g}=CV_{0}/2e$ شار بر روی خازن به واحدهای تعداد جفت کوپر است، $E_{C}=(2e)^{2}/2(C_{J}+C)$ انرژی بار است که مربوط به هر دو ظرفیت $C$ و ظرفیت اتصال جوزفسون $C_{J}$ است.	$H={\frac {q^{2}}{2C_{J}}}+\left({\frac {\Phi _{0}}{2\pi }}\right)^{2}{\frac {\phi ^{2}}{2L}}-E_{J}\cos \left[\phi -\Phi {\frac {2\pi }{\Phi _{0}}}\right]$ توجه داشته باشید که $\phi$ فقط اجازه دارد مقادیری بزرگتر از $2\pi$ بگیرد و به‌طور جایگزین به‌عنوان انتگرال زمانی ولتاژ در امتداد القاگر $L$ تعریف می‌شود.	$H={\frac {(2e)^{2}}{2C_{J}}}q^{2}-I_{0}{\frac {\Phi _{0}}{2\pi }}\phi -E_{J}\cos \phi$ در اینجا $\Phi _{0}$ کوانتوم شار مغناطیسی است.
انرژی پتانسیل	$U=-E_{J}\cos \phi$ . ولتاژ بایاس به‌طور تنظیم‌شده است به طوری که $N_{g}={\frac {1}{2}}$ باشد، که فاصله انرژی بین $|0\rangle$ و $|1\rangle$ را به حداقل می‌رساند و فاصله آن را از دیگر فاصله‌های انرژی (مانند فاصله بین $|1\rangle$ و $|2\rangle$) متمایز می‌کند. تفاوت در شکاف‌ها اجازه می‌دهد تنها انتقالات از $|0\rangle$ به $|1\rangle$ و بالعکس انجام شود، بدون اینکه حالات دیگر پر شوند.	$U=\left({\frac {\Phi _{0}}{2\pi }}\right)^{2}{\frac {\phi ^{2}}{2L}}-E_{J}\cos \left[\phi -\Phi {\frac {2\pi }{\Phi _{0}}}\right]$ ولتاژ شار مغناطیسی به $\Phi =\Phi _{0}/2$ بایاس شده است. چاه‌های پتانسیل مختلف مربوط به تعداد خاصی از کوانتوم‌های فلکس که در حلقه‌های ابررسانا محصور شده‌اند، می‌باشند. دو حالت پایین‌تر مربوط به ترکیب‌های متقارن و ضدمتقارن از صفر یا یک کوانتوم فلکس محبوس شده است که گاهی اوقات به‌عنوان حالات جریان حلقه در جهت عقربه‌های ساعت و خلاف جهت عقربه‌های ساعت نشان داده می‌شود: $|0\rangle =\left[|\circlearrowleft \rangle +|\circlearrowright \rangle \right]/{\sqrt {2}}$ و $|1\rangle =\left[|\circlearrowleft \rangle -|\circlearrowright \rangle \right]/{\sqrt {2}}$.	$U=-I_{0}{\frac {\Phi _{0}}{2\pi }}\phi -E_{J}\cos \phi$، که به‌عنوان «پتانسیل تخته‌شستن» شناخته می‌شود. جریان بایاس تنظیم شده است تا چاه‌هایی به‌قدری کم‌عمق باشند که دقیقاً دو تابع موج موضعی‌شده را دربر گیرند. افزایش جزئی در جریان بایاس باعث «ریزش» انتخابی حالت انرژی بالاتر ($|1\rangle$) می‌شود که با یک پیک ولتاژ قابل اندازه‌گیری بیان می‌شود (مکانیسمی که معمولاً برای اندازه‌گیری در مکانیک کوانتومی کیوبیت فاز استفاده می‌شود).

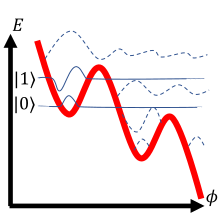در جدول بالا، سه نوع کیوبیت ابررسانا بررسی شده‌اند. در ردیف اول، نمودار مدار الکتریکی کیوبیت ارائه شده است. ردیف دوم یک هامیلتونی کوانتومی است که از مدار استخراج شده است. به‌طور کلی، هامیلتونی مجموع انرژی‌های جنبشی و پتانسیلی سیستم است (مشابه یک ذره در چاه پتانسیل). برای هامیلتونی‌های ذکر شده، $\phi$ تفاوت فاز تابع موج ابررسانای عبوری از تقاطع، $C_{J}$ ظرفیت وابسته به تقاطع جوزفسون، و $q$ بار روی ظرفیت تقاطع است. برای هر پتانسیل نشان داده شده، تنها از تابع موج‌های جامد برای محاسبه استفاده شده است. پتانسیل کیوبیت با خط قرمز ضخیم نشان داده شده و راه‌حل‌های تابع موج شماتیک با خطوط نازک به‌طور واضح به سطح انرژی مناسب خود منتقل شده‌اند.

توجه داشته باشید که جرم ذره معادل یک تابع وارون ظرفیت مدار است و شکل پتانسیل تحت تأثیر القاگرهای معمولی و تقاطع‌های جوزفسون قرار دارد. راه‌حل‌های شماتیک تابع موج در ردیف سوم جدول، دامنه پیچیده متغیر فاز را نشان می‌دهند. به‌طور خاص، اگر فاز کیوبیت در حالی که در یک وضعیت خاص قرار دارد اندازه‌گیری شود، احتمال غیر صفر برای اندازه‌گیری یک مقدار خاص فقط در جایی که تابع موج نشان داده شده نوسان می‌کند وجود دارد. هر سه ردیف اساساً نمایش‌های مختلفی از همان سیستم فیزیکی هستند.

کیوبیت‌های منفرد

فاصله انرژی هرتز بین سطوح انرژی یک کیوبیت ابررسانا به‌گونه‌ای طراحی شده که با تجهیزات الکترونیکی موجود سازگار باشد، به‌خاطر امواج تراهرتز (عدم وجود تجهیزات در باند طیفی بالاتر). نظریه بی‌سی‌اس نشان می‌دهد که حد بالای عملکرد در ~1THz است که فراتر از آن جفت‌های کوپر شکسته می‌شوند، بنابراین جداسازی سطوح انرژی نمی‌تواند خیلی زیاد باشد. از سوی دیگر، جداسازی سطوح انرژی نمی‌تواند خیلی کوچک باشد به‌دلیل ملاحظات سرمایشی: دمای ۱ کلوین نوسانات گرمایی ۲۰ گیگاهرتز را به همراه دارد. دماهای ده‌ها میلی‌کلوین در یخچال رقیق‌سازی به‌دست می‌آیند و اجازه می‌دهند که کیوبیت‌ها با جداسازی سطوح انرژی حدود ~۵ گیگاهرتز عمل کنند. جداسازی سطوح انرژی کیوبیت معمولاً با کنترل یک خط بایاس کردن اختصاصی تنظیم می‌شود، که «دستگیره‌ای» برای تنظیم دقیق پارامترهای کیوبیت فراهم می‌کند.

دروازه‌های کیوبیت منفرد

نمایش کره بلوخ

دروازه کیوبیت منفرد با چرخش در کره بلوخ انجام می‌شود. چرخش‌ها بین سطوح انرژی مختلف یک کیوبیت منفرد توسط پالس‌های ریزموج ارسال‌شده به یک آنتن یا خط انتقال متصل به کیوبیت که بسامد آن با جداسازی انرژی بین سطوح هم‌رزون است، القا می‌شوند. کیوبیت‌های منفرد ممکن است توسط یک خط انتقال اختصاصی یا یک خط انتقال مشترک اگر سایر کیوبیت‌ها در حالت تشدید (فیزیک) نباشند، آدرس‌دهی شوند. چرخش به دور محور ثابت توسط مدولاسیون کیوآام پالس ریزموج تنظیم می‌شود، در حالی که طول پالس تعیین‌کننده جابه‌جایی زاویه‌ای است.

به‌طور رسمی (بر اساس نشانه‌گذاری) برای یک سیگنال تحریک:

${\mathcal {E}}(t)={\mathcal {E}}^{x}(t)\cos(\omega _{d}t)+{\mathcal {E}}^{y}(t)\sin(\omega _{d}t)$

با بسامد $\omega _{d}$، هامیلتونی کیوبیت تحریک‌شده در تقریب موج چرخشی به صورت زیر است:

$H^{R}/\hbar =(\omega -\omega _{d})|1\rangle \langle 1|+{\frac {{\mathcal {E}}^{x}(t)}{2}}\sigma _{x}+{\frac {{\mathcal {E}}^{y}(t)}{2}}\sigma _{y}$،

که در آن $\omega$ رزونانس کیوبیت است و $\sigma _{x},\sigma _{y}$ ماتریس‌های پائولی هستند.

برای انجام یک چرخش حول محور $X$، می‌توان ${\mathcal {E}}^{y}(t)=0$ قرار داد و پالس ریزموج را با بسامد $\omega _{d}=\omega$ به مدت $t_{g}$ اعمال کرد. تبدیل حاصل عبارت است از:

$U_{x}=\exp \left\{-{\frac {i}{\hbar }}\int _{0}^{t_{g}}H^{R}dt\right\}=\exp \left\{-i\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt\cdot \sigma _{x}/2\right\}$.

این دقیقاً همان عملگر چرخش $R_{X}(\theta )$ با زاویه $\theta =\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt$ حول محور $X$ در کره بلوخ است. چرخش حول محور $Y$ به‌طور مشابه انجام می‌شود. نمایش دو عملگر چرخش کافی است تا همگنی را برآورده کند، زیرا هر عملگر واحدی کیوبیت منفرد $U$ می‌تواند به صورت $U=R_{X}(\theta _{1})R_{Y}(\theta _{2})R_{X}(\theta _{3})$ (تا یک فاز جهانی که از نظر فیزیکی بی‌اهمیت است) به نمایش درآید که به‌وسیله روشی به نام $X-Y$ تجزیه می‌شود. تنظیم $\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt=\pi$ منجر به تبدیل زیر می‌شود:

$U_{x}=\exp \left\{-i\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt\cdot \sigma _{x}/2\right\}=e^{-i\pi \sigma _{x}/2}=-i\sigma _{x}$

تا فاز جهانی $-i$ و به عنوان دروازه‌های منطقی کوانتومی شناخته می‌شود.

اتصال کیوبیت‌ها

توانایی اتصال کیوبیت‌ها برای پیاده‌سازی دروازه‌های منطقی کوانتومی دو کیوبیتی ضروری است. اتصال دو کیوبیت می‌تواند از طریق اتصال هر دو به یک مدار اتصال الکتریکی میانه حاصل شود. این مدار ممکن است یک عنصر ثابت (مانند خازن) باشد یا قابل کنترل (مانند اسکوئد) باشد. در حالت اول، دکوپلاژ (الکترونیک) کیوبیت‌ها در زمانی که دروازه خاموش است از طریق تنظیم کیوبیت‌ها به طوری که از هم‌رزون نباشند، حاصل می‌شود که منجر به تفاوت در شکاف‌های انرژی بین وضعیت‌های محاسباتی آن‌ها می‌شود. این رویکرد به‌طور ذاتی محدود به اتصال‌های همسایه نزدیک است زیرا یک مدار الکتریکی فیزیکی باید بین کیوبیت‌های متصل شده قرار گیرد. به‌طور قابل توجهی، اتصال همسایه نزدیک در دی-ویو سیستمز یک سلول واحد با ۸ کیوبیت در پیکربندی گراف شیمیرا را به‌طور بسیار متصل ایجاد می‌کند. الگوریتم کوانتومیها معمولاً نیاز به اتصال بین کیوبیت‌های دلخواه دارند. در نتیجه، انجام چندین دروازه‌های منطقی کوانتومی ضروری است که طول محاسبات کوانتومی ممکن را پیش از ناهمدوسی کوانتومی پردازنده محدود می‌کند.

اتوبوس کوانتومی

یکی دیگر از روش‌های اتصال دو یا چند کیوبیت از طریق اتوبوس کوانتومی است که کیوبیت‌ها به این واسطه متصل می‌شوند. بوس کوانتومی معمولاً به‌عنوان یک حفره میکروویو مدل شده به‌عنوان یک نوسانگر هارمونیک کوانتومی پیاده‌سازی می‌شود. کیوبیت‌های متصل ممکن است به‌طور متناوب از هم‌رزون با بوس و با یکدیگر خارج شوند که محدودیت همسایگی را از بین می‌برد. فرمالیسم توصیف‌کنندهٔ اتصال، الکترودینامیک کوانتومی حفره‌ای است. در الکترودینامیک کوانتومی حفره‌ای، کیوبیت‌ها مشابه اتم‌هایی هستند که با یک کاواک اپتیکی با تفاوتی در محدوده گیگاهرتز (برخلاف رژیم ترهادز تابش الکترومغناطیسی) تعامل دارند. تبادل تحریک هم‌رزون بین این اتم‌های مصنوعی پتانسیل دارد که برای پیاده‌سازی مستقیم دروازه‌های چند کیوبیتی مفید باشد. با پیروی از حالت تاریک منیفلد (هندسه), طرح خازالی-مولمر عملیات پیچیده چند کیوبیتی را در یک گام انجام می‌دهد و این امکان را فراهم می‌آورد که به‌طور قابل توجهی مدل مداری سنتی را کوتاه کند.

دروازه‌های تشدید متقابل

یکی از مکانیزم‌های محبوب دروازه‌گذاری، استفاده از دو کیوبیت و یک بوس است که هرکدام به تفکیک سطوح انرژی متفاوت تنظیم می‌شوند. اعمال تحریک میکروویو به کیوبیت اول که با فرکانس هماهنگ با کیوبیت دوم است، باعث چرخش $\sigma _{x}$ در کیوبیت دوم می‌شود. جهت چرخش بستگی به وضعیت کیوبیت اول دارد و این امکان ساخت یک دروازه‌های منطقی کوانتومی را فراهم می‌کند.

با پیروی از نوتیشن، همیلتونیان رانش سیستم برانگیخته از طریق خط رانش کیوبیت اول به‌طور رسمی به صورت زیر نوشته می‌شود:

$H_{D}/\hbar =A(t)\cos({\tilde {\omega }}_{2}t)\left(\sigma _{x}\otimes I-{\frac {J}{\Delta _{12}}}\sigma _{z}\otimes \sigma _{x}+m_{12}I\otimes \sigma _{x}\right)$

که در آن $A(t)$ شکل پالس میکروویو در زمان، ${\tilde {\omega }}_{2}$ فرکانس هم‌رزون کیوبیت دوم، $\{I,\sigma _{x},\sigma _{y},\sigma _{z}\}$ ماتریس‌های پائولی، $J$ ضریب اتصال بین دو کیوبیت از طریق رزوناتور، $\Delta _{12}\equiv \omega _{1}-\omega _{2}$ تفاوت فرکانس کیوبیت‌ها، $m_{12}$ اتصال اضافی (غیرخواسته) بین کیوبیت‌ها و $\hbar$ ثابت پلانک است. انتگرال زمانی روی $A(t)$ زاویه چرخش را تعیین می‌کند. چرخش‌های غیرخواسته از اولین و سومین عبارت همیلتونیان می‌توانند با عملیات کیوبیت تکمیل شوند. مؤلفه باقی‌مانده، همراه با چرخش‌های کیوبیت تک، مبنایی برای su(4) جبر لی تشکیل می‌دهد.

دروازه فاز هندسی

سطوح بالاتر (خارج از فضای فرعی محاسباتی) یک جفت مدار ابررسانا متصل می‌توانند برای القای فاز هندسی بر یکی از حالت‌های محاسباتی کیوبیت‌ها استفاده شوند. این منجر به یک تغییر فاز شرطی در هم‌تنیدگی حالت‌های مرتبط کیوبیت‌ها می‌شود. این اثر از طریق تنظیم جریان فلکس طیف کیوبیت‌ها و از طریق استفاده از رانش میکروویو انتخابی پیاده‌سازی شده است. رانش غیر هم‌رزون می‌تواند برای القای تغییرات تفاوتی در شیفت استارک متناوب استفاده شود که امکان پیاده‌سازی دروازه‌های کنترل‌شده فاز کاملاً میکروویوی را فراهم می‌آورد.

تعاملات هایزنبرگ

مدل هایزنبرگ تعاملات، که به صورت زیر نوشته می‌شود:

${\hat {\mathcal {H}}}_{\mathrm {XXZ} }/\hbar =\sum _{i,j}J_{\mathrm {XY} }({\hat {\sigma }}_{\text{x}}^{i}{\hat {\sigma }}_{\text{x}}^{j}+{\hat {\sigma }}_{\text{y}}^{i}{\hat {\sigma }}_{\text{y}}^{j})+J_{\mathrm {ZZ} }{\hat {\sigma }}_{\text{z}}^{i}{\hat {\sigma }}_{\text{z}}^{j}$,

به عنوان مبنای شبیه‌سازی کوانتومی آنالوگ سیستم‌های اسپین و آغازگر مجموعه‌ای از دروازه‌های کوانتومی بیان‌گر عملگرهای "شبیه‌سازی فرمیونی" (یا دروازه‌های "fSim") عمل می‌کند. در مدارهای ابررسانا، این مدل تعامل با استفاده از کیوبیت‌های تنظیم‌پذیر از نظر جریان فلکس با کوپلینگ تنظیم‌پذیر پیاده‌سازی شده و امکان نمایش برتری کوانتومی را فراهم کرده است. علاوه بر این، این مدل می‌تواند در کیوبیت‌های ثابت‌فرکانس با کوپلینگ ثابت با استفاده از درایوهای میکروویو نیز پیاده‌سازی شود. خانواده دروازه‌های fSim شامل واحدهای دوکیوبیتی XY و ZZ دلخواه است، از جمله دروازه‌های iSWAP, CZ و SWAP (به دروازه‌های منطقی کوانتومی مراجعه شود).

پیوند به بیرون

• IBM Quantum offers access to over 20 quantum computer systems.
• The IBM Quantum Experience offers free access to writing quantum algorithms and executing them on 5 qubit quantum computers.
• IBM's roadmap for quantum computing shows 65 qubit systems available in 2020 and 127 qubits to be available sometime in 2021.