موجک

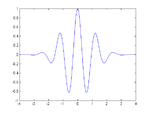
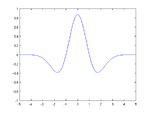
موجک (به انگلیسی: Wavelet) دسته‌ای از توابع ریاضی هستند که برای تجزیه سیگنال پیوسته به مؤلفه‌های فرکانسی آن بکار می‌رود که رزولوشن هر مؤلفه برابر با مقیاس آن است. تبدیل موجک تجزیه یک تابع بر مبنای توابع موجک می‌باشد. موجک‌ها (که به عنوان موجک‌های دختر شناخته می‌شوند) نمونه‌های انتقال یافته و مقیاس شده یک تابع (موجک مادر) با طول متناهی و نوسانی شدیداً میرا هستند. چند نمونه موجک مادر در شکل زیر نمایش داده شده‌اند.

مِیِر

مورله

کلاه مکزیکی

تبدیل‌های موجک

تعداد زیادی تبدیل موجک وجود دارد که لیست آن را می‌شود در فهرست تبدیل‌های مرتبط با موجک مشاهده نمود. معمول‌ترین این تبدیل‌ها عبارتند از:

• تبدیل موجک پیوسته (Continuous wavelet transform (CWT
• تبدیل موجک گسسته Discrete wavelet transform (DWT)
• تبدیل سریع موجک Fast wavelet transform (FWT)
• Lifting scheme
• تجزیه بسته‌های موجکWavelet packet decomposition (WPD)
• تبدیل موجک ساکن Stationary wavelet transform (SWT)

موجک‌ها و معادلات تاخیر

موجک‌ها بر مبنای دو عمل اصلی قرار دارند:

• انتقال (Translation)

$W(x)-->W(x+a)\!$

• پهن شدگی (Dilation)

$W(x)-->W(bx)\!$

مقایسه با تبدیل فوریه

در مقایسه با تبدیل فوریه می‌توان گفت که تبدیل موجک دارای خصوصیت محلی‌سازی بسیار خوبی است. به‌طور مثال تبدیل فوریه یک پیک تیز دارای تعداد زیادی ضریب است، چرا که توابع پایه تبدیل فوریه توابع سینوسی و کسینوسی هستند که دامنه آن‌ها در کل بازه ثابت است، در حالی که توابع موجک توابعی هستند که بیشتر انرژی آن‌ها در بازه کوچکی متمرکز شده‌است و به سرعت میرا می‌شوند. بنابراین با انتخاب مناسب موجک‌های مادر می‌توان فشرده‌سازی بهتری در مقایسه با تبدیل فوریه انجام داد.

تاریخچه

در تاریخ ریاضیات مبادی و ریشه‌های متعددی را می‌توان برای موجک‌ها سراغ گرفت.

کارهای قبل از ۱۹۳۰

مربوط به قبل از ۱۹۳۰ (م) می‌توان به آنالیز فرکانس‌ها اشاره کرد، که به وسیلهٔ فوریه شروع شد.

استفاده از واژهٔ موجک‌ها، برای اولین بار، در یکی از ضمیمه‌های تز آلفرد هار (۱۹۰۹ م) ظاهر شد. امروزه هم، این موجک‌ها به همان نام یعنی به موجک‌های هار معروف‌اند. موجک‌های هار دارای دامنهٔ تعریف فشرده (compact) بوده، و غیر مشتق‌پذیر به صورت پیوسته هستند.

کارهای مربوط به دهه ۱۹۳۰

در این دهه چند گروه پیرامون موضوع نمایش توابع با به‌کارگیری پایه‌های با مقیاس متغیر برای تنیدن فضاهای توابع تحقیق می‌نمودند.

موجک‌های متعامد

مقالهٔ اصلی: موجک‌های متعامد

با دیدی کلی می‌توان اظهار داشت که پایه‌های متعامد حالتی بهینه برای تنیدن فضاهای برداری (چه فضاهای با ابعاد متناهی و چه فضاهای بی‌نهایت بعدی) و انجام محاسبات ارائه می‌نمایند. لذا همواره تمایل و تلاش در این راستا قرار داشته که یا مجموعه پایه‌ها از آغاز متعامد انتخاب شود یا آن که با شیوه‌هایی نظیر گرام اشمیت آن‌ها را به سوی تعامد سوق داد.

موجک هار

مقالهٔ اصلی: موجک هار

موجک هار اولین موجک شناخته شده می‌باشد که پیدایش آن به سال‌های ابتدای قرن بیستم باز می‌گردد. این موجک ساده‌ترین نوع هم هست و پایه‌هایی متعامد برای تنیدن فضای محاسبه را ارائه می‌دهد. mz

جستارهای وابسته

• تبدیلات فوریه
• حسابان تغییرها
• موجک‌های متعامد

منابع

• موجک‌ها و بانک‌های فیلترها، گیلبرت استرنگ (انگلیسی)
• مشارکت‌کنندگان ویکی‌پدیا. «Wavelet». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۱۸ مارس ۲۰۰۸.

پیوند به بیرون

• مقالات نسبتاً ساده و گویا، پیرامون موجک‌ها، گیلبرت استرنگ Gilbert Strang
• ده سخنرانی در بارهٔ موجک‌ها (انگلیسی)
• تمرین با موجک‌های گوناگون به صورت بصری بایگانی‌شده در ۱۸ مه ۲۰۰۸ توسط Wayback Machine (انگلیسی)

توصیف: اپلت موجود موجک‌های گوناگونی را به همراه توابع مقیاس شان به تصویر می‌کشد