استخوان مصنوعی

استخوان مصنوعی ( Artificial bone )

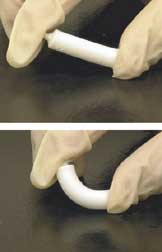
استخوان مصنوعی به مواد استخوان مانندی گفته می‌شود که در آزمایشگاه ایجاد می‌شوند و می‌توان از آنها در پیوندهای استخوانی استفاده کرد تا جایگزین استخوان انسانی که به دلیل شکستگی‌های شدید، بیماری و غیره از بین رفته است شوند.

از پیوندهای استخوانی می‌توان به استفاده از نسج استخوان قسمتی از بیمار برای قسمتی دیگر (اتوگرافت) و استفاده از نسج استخوان از فردی دیگر (آلوگرافت) اشاره کرد. به علت عوارض و محدودیت در میزان استخوان و همچنین به علت عوارض و مشکلات تهیه آلوگرافت، پیوند مطلوب و ایده آل اتوگرافت می باشد. با استفاده از ترکیبات مصنوعی استخوان، تحولی در ترمیم نقص‌های استخوانی ایجاد شده‌است. استخوان مصنوعی یکی از انواع این ترکیبات است که در مقایسه با سایر ترکیبات مصنوعی کاربرد ساده‌تر دارد و در کشور ما راحت‌تر از سایر ترکیبات در دسترس می‌باشد. در محدودهٔ زمانی یک ساله و طی یک مطالعه توصیفی _تحلیلی،تعدادی بیماران دچار بیماری های استخوانی که اندیکاسیون مصرف پیوند استخوان را داشتند و داوطلب استفاده از پیوند استخوان مصنوعی بودند، انتخاب شدند. پس از بررسی ۶۲نفر (۵۰نفر مرد و۱۲نفر زن) مورد مطالعه قرار گرفته، فرمهای مربوط تکمیل شد و بیماران تحت عمل پیوند استخوان مصنوعی قرار گرفتند. در هفته‌ های چهارم، دهم و بیستم پس از عمل جراحی از نظر نتایج درمانی و جوش خوردگی بررسی شدند. از ۶۲ نفر مورد مطالعه، در ۶ نفر از بیماران پس از هفته بیستم کال استخوانی تشکیل نگردید. بدین ترتیب در ۷/۹ درصد درمان به روش استخوان مصنوعی با عدم موفقیت روبرو شد. میانگین سنی بیماران ۵/۳ ± ۳۳ سال بود که پس از تشکیل گروه‌ های سنی تفاوت معنی داری از نظر زمان تشکیل کال استخوان وجود داشت. زمان تشکیل کال استخوان در گروه‌های سنی پایین‌‌تر در مقایسه با گروه‌ های سنی بالاتر زودتر بود. در هیچ‌ یک از بیماران عوارض عفونی و غیر عفونی مشاهده نشد. در این مطالعه علاوه بر استفاده از استخوان مصنوعی به تنهایی در بعضی از بیماران خاص مثل عدم جوش خوردن‌ های مشکل استخوان و کیست‌ های استخوانی، از استخوان مصنوعی همراه با آلوگرافت استفاده شد با توجه به تشکیل کال استخوانی و نتایج مطلوب در ۳/۹۰ درصد از بیماران، مصرف این ماده به تنهایی و یا در موارد خاص به صورت ترکیب با اتوگرافت ویا آلوگرافت در بیماریهای استخوان پیشنهاد می‌شود.

پروتزها

پروتز به یک وسیله مصنوعی می‌گویند که جایگزین یک قسمت از دست رفته بدن می‌شود. گرچه وسایل مصنوعی در قسمت‌ های مختلفی از بدن بکار می‌روند ولی در ارتوپدی منظور از پروتز بیشتر اندام مصنوعی است. البته سر مصنوعی استخوان ران که از جنس فلز بوده و در شکستگی‌های گردن استخوان ران از آن استفاده می‌شود را هم پروتز می‌نامند. پروتز یک مادهٔ سیلیکونی است که در بازارهای جهانی وجود دارد و در دسترس است. این پروتز برای فرم‌دهی یا در زمینهٔ زیبایی‌‌شناسی برای برجسته کردن اندام مورد استفاده قرار می‌گیرد که مورد استقبال عموم قرار گرفته و می‌توان در اکثر نقاط بدن بدون محدودیت استفاده کرد. پروتز برای بیماران زیادی تجویز می‌شود؛ از جمله برای بیماران سرطانی که بعد از پایان دورهٔ درمانشان متأسفانه سینهٔ خود را از دست می‌دهند و افرادی که بر اثر تصادف چانه و فک خود را از دست می‌دهند یا دچار شکستگی گونه می‌شوند هم پیشنهاد می‌شود. پروتز علاوه بر جراحی‌های ضروری، در زمینهٔ زیبایی‌شناسی پزشکی هم طرفداران زیادی دارد. پروتز یا اندام مصنوعی را در مواردی بکار می‌برند که قسمتی از اندام به علتی وجود ندارد قسمتی از اندام ممکن است به‌صورت مادرزادی وجود نداشته باشد قسمتی از اندام ممکن است بدنبال آسیب‌های شدید ناشی از ضربه از بین برود قسمتی از اندام ممکن است به علت بیماری مانند دیابت از بین برود. در سال‌های اخیر با استفاده از فیبر کربن (که بسیار محکم و در عین حال سبک است) و همچنین با پیشرفت دانش الکترونیک گام‌های بلندی در بهتر کردن اندام‌های مصنوعی برداشته شده است.

داربست

مروری بر برخی از مدلهای ارائه شده برای محاسبه خواص مکانیکی مواد متخلخل

به دلیل متخلخل بودن داربستهای استخوانی، می‌توان از روش‌های به کاررفته در مدلسازی مواد متخلخل برای به دست آوردن خواص مکانیکی آن‌ها استفاده کرد. در سال‌های اخیر روابط زیادی چه به صورت تجربی و چه به‌صورت تحلیلی برای به دست آوردن خواص الاستیک مؤثر مواد متخلخل پیشنهاد شده‌است. روش‌های تحلیلی ارائه شده را می‌توان در حالت کلی به دو دسته تقسیم کرد. دسته نخست از این روش‌ها براساس تئوری‌های مربوط به مواد کامپوزیتی است. در این گروه از مدل‌ها قطعه به صورت حالت خاصی از یک ماده کامپوزیتی دوفازی در نظر گرفته می‌شود که یک فاز از آن (تخلخل) دارای سفتی صفر است. دسته دوم از این مدل‌ها مربوط به جامدهای سلولی است. این مدل‌ها براساس روش‌های حداقل سطح جامد ۱ کارمی‌کنند و در آن‌ها ماده به صورت تک فاز در نظر گرفته می‌شود که حفره‌هادر آن نفوذ کرده‌اند. در این بخش برخی از مهمترین مدلهای مربوط به‌محاسبه خواص الاستیک مؤثر مواد متخلخل ارائه می‌شوند. باید توجه شود به ترتیب بیانگر مدول یانگ، ضریب 𝜌 و 𝜙، 𝜇، 𝜅، 𝜈، 𝐸، که در روابط زیرپواسون، مدول حجمی، مدول برشی، درصد تخلخل و چگالی است، همچنین نیز نشان می‌دهد که کمیت مورد نظر به ترتیب به ماده 𝑝 و 𝑠 زیرنویس سازنده (ماده بدون تخلخل از همان جنس) و ماده متخلخل مربوط است.

مدل راماکریشنان و آروناچالام

راماکریشنان و آروناچالام مدلی را برای محاسبه مدول یانگ مواد متخلخل پیشنهاد کردند که از دقت مناسبی برای تخلخل‌های کمتر از % ۴۰برخوردار است. این مدل حالت خاصی از فرمول بندی ارائه شده برای موادکامپوزیتی دوفازی نیست و صرفاً برای شبیه سازی مواد متخلخل ارائه شده‌است.

مدل وانگ و تیسنگ

وانگ و تیسنگ مدلی را برای تخمین خواص مکانیکی مؤثر مواد کامپوزیتی دو فازی حاوی ذرات کروی با توزیع تصادفی ارائه دادند. این محققان با استفاده از نتایج مدل پیشنهادی به استخراج عباراتی تحلیلی و صریح برای خواص مؤثر مواد متخلخل برحسب خواص مکانیکی ماده سازنده و درصد تخلخل آنها پرداختند. مطابق این مدل مدول حجمی و مدول برشی مؤثر یک ماده متخلخل بیان می‌شود.

روش دیفرانسیلی

است که منجر به کاهش 𝜙 هدف روش دیفرانسیلی غلبه بر محدودیت ۱کاربرد روش تخمین رقیق شده‌است. ایده اصلی این روش اضافه کردن تدریجی و مرحله به مرحله تخلخل به ماده سازنده تا زمان دستیابی به درصد تخلخل نهایی است. در هر مرحله نیز از روش تخمین رقیق برای بهدست آوردن خواص مکانیکی مؤثر ماده به دست آمده استفاده می‌شود. بدین منظور ابتدا درصد بسیار کوچکی از تخلخل به ماده سازنده اعمال و خواص مؤثر ماده حاصل با استفاده از روابط) ۱۹٬۱۸ (محاسبه می‌شود. در ادامه بخش بسیار کوچکی از ماده حاصل (شامل تخلخل) جدا شده و به جای آن به همان اندازه تخلخل جایگزین می‌شود و دوباره از روش تخمین رقیق برای به دست آوردن خواص مکانیکی ماده جدید که حاوی تخلخل بیشتری است نسبت به ماده پیشین استفاده می‌شود. تکرار پروسه جداسازی ماده و اضافه کردن تخلخل منجر به دستیابی به دو معادله دیفرانسیل کوپل شده برای محاسبه مدولهای حجمی و برشی مؤثر ماده متخلخل می‌شود.

روش تخمین رقیق

روش تخمین رقیق در اصل برای مواد کامپوزیتی با درصد حجمی بسیار ناچیز ذرات پیشنهاد شده‌است. همان‌طور که پیشتر نیز بدان اشاره شد، مواد متخلخل را می‌توان حالت خاصی از مواد کامپوزیتی در نظر گرفت که یک فاز از آن دارای سفتی صفر است. به همین دلیل از روش تخمین رقیق نیز می‌توان برای به دست آوردن خواص مکانیکی مواد متخلخل با درصد استفاده کرد. باید توجه شود که برای استفاده از این 𝜙 (تخلخل پایین) ۱روش درصد تخلخل باید به اندازه‌های کوچک باشد که بتوان از برهمکنش مکانیکی میان حفره‌ها صرف نظر کرد. با فرض شکل کروی برای حفره‌ها، مدول‌های حجمی و برشی یک ماده متخلخل با استفاده از روش تخمین رقیق به دست می‌آیند.

روشهای همگنسازی میکرومکانیکی

روش‌های همگن سازی میکرومکانیکی نیز مانند روش تخمین رقیق در اصل برای مواد کامپوزیتی پیشنهاد شده‌اند، اما می‌توان از آنها برای محاسبه خواص مکانیکی مواد متخلخل نیز استفاده کرد. نکته‌ای که در مورد این روش‌ها باید بدان توجه شود آن است که در اینجا، برخلاف روشهای یپیشین، تنها خواص مکانیکی مؤثر ماده متخلخل بهدست نمی‌آید، بلکه این روش‌ها امکان محاسبه کامل ماتریس سفتی ماده را فراهم می‌آورند. برخلاف اکثر روش‌های مورد بررسی قرار گرفته، در اینجا تأثیر شکل ذرات (حفره‌ها) نیز در بهدست آوردن خواص به خوبی لحاظ می‌شود. روش‌های خودسازگاری و موری- تاناکا از جمله مهمترین روش‌های همگنسازی میکرومکانیکی است.

مدلسازی داربستهای استخوانی

در حالت کلی داربستهای استخوانی به صورت تک جنسه یا چند جنسه(کامپوزیتی) ساخته می‌شوند که مدل‌سازی آن‌ها به ترتیب به صورت تک مقیاسه و چند مقیاسه انجام می‌گیرد. در این بخش ضمن توضیح این روش‌ها به معرفی داربست‌های استخوانی تک جنسه و دو جنسه و نحوه مدلسازی آن‌ها پرداخته خواهد شد. همان‌طور که پیش تر بدان اشاره شد برای شبیه‌سازی داربست‌های تک جنسه از روش تک مقیاسه استفاده می‌شود. در این روش خواص مکانیکی داربست‌ها استخراج می‌شود. در این بخش به منظور بررسی ومقایسه عملکرد مدلهای مختلف ارائه شده خواص مکانیکی داربستهای تک جنسه ساخته شده از مواد گوناگون سرامیکی درتخلخل‌های مختلف با استفاده از این مدلها و به کمک روش تک مقیاسه در نظر گرفته شده انده، به دست آمدهاند. در مدلسازی داربستهای مختلف شکل حفره‌ها کروی و شکل ذرات و بغدادیت، به ترتیب سوزنی CEL هیدروکسی آپاتیت، سرامیک شیشه، دیسکی شکل و در نظر گرفته شده‌است. علاوه بر داربستهای تک جنسه از روابط میکرومکانیکی ارائه شده برای شبیه‌سازی داربست‌های استخوانی کامپوزیتی متخلخل نیز می‌توان استفاده‌کرد. این داربست‌ها از ماتریسی از جنس کلاژن که حاوی نسبتهای حجمی مختلف از ذرات کروی شکل هیدروکسی آپاتیت است، ساخته شده و مدول یانگ آنها در تخلخلهای مختلف بااستفاده از روش اجزای محدود بهدست آمده‌است. برای به دست آوردن خواص مکانیکی این داربست‌ها به صورت تئوری باید از روش مدل‌سازی چند مقیاسه استفاده کرد. در این روش از اطلاعات مقیاس پایین‌تر برای محاسبه خواص مقیاس بالاتر استفاده می‌شود. بدین معنی که خروجی هرمقیاس به عنوان ورودی برای مقیاس بالاتر مورد استفاده قرار می‌گیرد. محاسبه خواص مکانیکی داربستهای استخوانی سرامیکی (مدلسازی تک مقیاسه) از میان دو روش همگن سازی میکرو مکانیکی ارائه شده تنها از روش خود سازگاری برای به دست آوردن مدول یانگ این داربست‌ها استفاده شده واز روش موری- تاناکا صرف نظر شده‌است. دلیل این امر آن است که ساختاراین داربست‌ها به گونه ای است که در آنها امکان مشخص کردن دقیق یک فاز به عنوان فاز ماتریس وجود ندارد و بنابراین روش خود سازگاری تخمین بهتری از خواص مکانیکی آنها فراهم می‌آورد. به منظور مقایسه بهتر مقادیر آزمایشگاهی مربوط نیز در هر مورد بیان شده‌اند. ۶ مدل دیوی برای تخلخلهای کمتر از - شکلهای ۲۳۰٪ بسیار مناسب است، اما با افزایش تخلخل دقت آن کاهش می‌یابد. خصوصاً که دارای تخلخل‌های به نسبت بالایی است، این مدل کارایی لازم را ندارد. این مدل برای تخلخل‌های بالای % ۵۰ توانایی محاسبه مدول یانگ را ندارد. این مدل در حقیقت برای تخمین مدول یانگ در حالت رقیق (برای تخلخلهای پایین) پیشنهاد شده‌است. عملکرد روش تخمین رقیق تا حدود زیادی مشابه روش دیوی است واختلاف نتایج بهدست آمده از این روشها در تخلخل‌های مختلف کمتر از % ۲ است. دقت این روش نیز با افزایش تخلخل به شدت کاهش می‌یابد و مشابه مدل دیوی برای تخلخل‌های بالای % ۵۰ امکان استفاده از این روش برای محاسبه مدول یانگ وجود ندارد. مقادیر بهدست آمده از این دو مدل تا حدود زیادی مشابه هم است و از مدل تخمین رقیق نیز می‌توان مانند روش دیوی برای محاسبه مدول یانگ مواد متخلخل با تخلخل زیر % ۳۰ استفاده کرد. برخلاف روشهای دیوی و تخمین رقیق عملکرد روشهای رایس و دیفرانسیلی با افزایش درصد تخلخل بهبود می‌یابند. روش رایس در میان روش‌های مورد بررسی دارای بدترین عملکرد است (به ویژه برای تخلخل‌های پایین) و مقادیر به دست آمده از این روش اختلاف زیادی با یافته‌های آزمایشگاهی دارند. روش دیفرانسیلی حتی در تخلخل‌های پایین نیز عملکرد قابل قبولی دارد. باید توجه شود که روش دیفرانسیلی برای برطرف کردن محدودیت‌های روش تخمین رقیق در پیش‌بینی خواص مکانیکی مواد با تخلخل بالا ارائه شده‌است و از فرمول بندی این روش برای محاسبات استفاده می‌نماید. به همین دلیل در تخلخلهای پایین (زیر % ۱۰)مقادیر به دست آمده از روش‌های تخمین رقیق و دیفرانسیلی بسیار مشابه است، اما برای تخلخلهای بالا (به ویژه بالای % ۵۰)، روش دیفرانسیلی قادر به پیشبینی مناسب مدول یانگ داربست هاست. برای داربستهای استخوانی حداکثر میزان خطای میان CEL ساخته شده از جنس سرامیک شیشه به دست آمده با این روش با یافته‌های آزمایشگاهی برابر % ۲۰ است. عملکرد مدله ای گیبسون، رابرتس و گربوزی و وانگ و تیسنگ در پیشبینی مدول یانگ تقریباً یکسان است. این مدلها معمولاً در تخلخلهای پایین مقادیری با % ۲۰ خطا نسبت به یافته‌های آزمایشگاهی برای مدول یانگ ارائه می‌دهند. برای تخلخلهای بالای % ۲۰ روش هراکوویچ و بکستر نیز مقادیری تقریباً مشابه این روشها برای مدول یانگ به دست می‌دهد. روش خود سازگاری یکی از بهترین مدل‌های بررسی شده‌است که کارایی مناسبی در محاسبه مقادیر مدول یانگ داربست‌های استخوانی سرامیکی از خود نشان می‌دهد. در تخلخلهای پایین (زیر % ۲۰) مقدار حداکثر میزان اختلاف مقادیر به دست آمده با این روش و نتایج آزمایشگاهی در حدود % ۸ است. با افزایش تخلخل داربستها دقت این مدل تا حدودی کاهش می‌یابد، اما با این وجود استفاده از این روش برای تخلخل‌های بالا نیز منجر به دستیابی به مقادیر قابل قبولی برای مدول یانگ می‌شود که دارای دقتی نزدیک به روش دیفرانسیلی است. مقادیر به دستآمده برای ضریب پواسون داربست استخوانی ساخته شده از جنس هیدروکسی آپاتیت با استفاده از روشهای رابرتس و گربوزی، وانگ و تیسنگ، تخمین رقیق، دیفرانسیلی و خودسازگاری در تخلخلهای مختلف رسم شده‌اند. تنها مقادیر آزمایشگاهی در دسترس برای ضریب پواسون که توسط دویس و همکاران برای داربستهای از از میان مدلهای مورد بررسی بهترین عملکرد در محاسبه ضریب پواسون برای تخلخل‌های کمتر از % ۱۰درصد متعلق به روش رابرتس و گربوزی (با حداکثر % ۲٫۶ خطا) و برای‌تخلخلهای بالاتر از % ۱۰ متعلق به روش خودسازگاری (با حداکثر % ۲٫۵ خطا) است. اختلاف مقادیر به دست آمده از مدلهای مختلف برای ضریب پواسون بسیار ناچیز است.

محاسبه خواص مکانیکی داربستهای استخوانی کامپوزیتی (مدلسازی چند مقیاسه)

نسبتهای حجمی مختلف از ذرات هیدروکسی آپاتیت نشان داده شده‌است. تحلیل در این مرحله با استفاده از روش همگنسازی میکرومکانیکی موری- تاناکا انجام گرفته‌است. دلیل انتخاب روش موری- تاناکا آن است که ساختار این داربستها به گونه‌های است که در آنها امکان مشخص کردن دقیق یک فاز (کلاژن) به عنوان فاز ماتریس وجود دارد، بنابراین این روش تخمین مناسبی از خواص مکانیکی آنها فراهم می‌کند. در این محاسبات شکل ذرات هیدروکسی آپاتیت به صورت کروی در نظر گرفته شده‌است. به منظور مقایسه مقادیر مدول یانگ کامپوزیت‌های هیدروکسی آپاتیت و کلاژن به دست آمده توسط چان و همکارانش با استفاده از روش اجزای محدود نیز در این شکل نشان داده شده‌است. مطابقت مناسبی میان یافته‌های این تحقیق و داده‌های عددی ارائه شده در مقاله برای کامپوزیتهای سازنده داربستهای استخوانی در شکل ۸ قابل مشاهده است. حداکثر مقدار خطا در شکل ۸ مربوط به نسبت حجمی % ۷۵ هیدروکسی آپاتیت که برابر با % ۴ است. از نتایج به دستآمده در مرحله اول به عنوان ورودی (خواص مکانیکی ماده سازنده) برای یافتن مدول یانگ نهایی داربست‌های متخلخل استفاده می‌شود. تخلخلها در این محاسبات مطابق مقاله به صورت کروی شکل در نظر گرفته شده‌اند. به دلیل قابل تشخیص بودن دقیق یک فاز به عنوان فاز ماتریس از میان دو روش همگن سازی میکرو مکانیکی ارائه شده از روش موری- تاناکا برای به دست آوردن مدول یانگ این داربستها استفاده شده و از روش خودسازگاری صرف نظر شده‌است. نتایج نشان می‌دهند که استفاده از روش ارائه شده در به دست آوردن خواص مکانیکی داربست‌های کامپوزیتی نیز منجر به دستیابی به نتایج قابل قبولی می‌شود. هر چند که در این حالت به دلیل چند مقیاسه بودن تحلیل و جمع شدن خطاها در مراحل مختلف درصد خطا اندکی بالاتر از مسائل تکم قیاسه است. البته باید توجه شود که چون محدوده تخلخل‌ها کمتر از % ۳۰ است عمده خطا ناشی از افزایش درصد حجمی هیدروکسی آپاتیت است، به‌طوری که کمترین دقت مربوط به داربست‌هایی است که دارای % ۸۰ حجمی هیدروکسی آپاتیت است. بررسی مقادیر ارائه برای مدول یانگ نشان می‌دهد که به دلیل محدوده تخلخل‌های مورد بررسی تفاوت میان مقادیر به دست آمده از مدل‌های مختلف بسیار ناچیز است. هرچند دقت روشهای دیفرانسیلی و موری- تاناکا خصوصاً در تخلخلهای بالاتر اندکی بیش از دیگر روشهاست.

مدلسازی آماری خواص مکانیکی داربستهای استخوانی ازجنس هیدروکسی آپاتیت

با توجه به کاربرد گسترده هیدروکسی آپاتیت در ساخت داربست‌های استخوانی در این قسمت نتایج به دست آمده برای خواص مکانیکی این گونه داربست‌ها مورد تجزیه و تحلیل آماری قرار گرفته و رابطه میان درصد تخلخل و مدول یانگ و ضریب پواسون آنها استخراج خواهد شد. بدین منظور برای بهدست آوردن خواص این نوع داربست ها در محدوده‌های مختلف تخلخل شناسایی خواهند شد و سپس از مدل شناسایی شده در هر بازه، برای به دست آوردن خواص در همان بازه استفاده می‌شود. پس از به دست آوردن خواص مکانیکی داربست در تخلخل‌های مختلف با استفاده از نرم‌افزار اسپی اساس، فرمولهای رگرسیون مختلف برای خواص مکانیکی و تخلخل معین شده و ضرایب رگرسیون و تعیین برای حالات مختلف بررسی خواهند شد.

بررسی مقادیر به دست آمده برای مدل یانگ داربست‌های استخوانی نشان می‌دهد که (ساخته شده از جنس هیدروکسی آپاتیت از میان روشهای مورد بررسی) دقت مدل‌های دیوی و خودسازگاری برای تخلخل‌های زیر % ۳۰ بیشتر از سایر مدل هاست. به دلیل سادگی روش دیوی و عدم وجود تفاوت چشم گیر میان نتایج به دست آمده از این دو روش، استفاده از روش دیوی در این محدوده از تخلخلها دارای ارجحیت است. دقت روش (برای تخلخل های % ۳۰ تا % ۶۰) بیش از سایر روش هاست و همچنین برای تخلخلهای بالای ۶۰٪ نیز تطابق مناسبی میان نتایج روش دیفرانسیلی و داده‌های آزمایشگاهی مشاهده می‌شود. در مورد ضریب پواسون نیز هر چند تفاوت آشکاری میان نتایج روش‌های رابرتس و گربوزی، دیفرانسیلی و خودسازگاری مشاهده نمی‌شود، اما روش خودسازگاری به دلیل دقت بالاتر برای محاسبات انتخاب می‌شود.

با به دست آوردن مقادیر خواص مکانیکی داربست ها در تخلخل های مختلف با استفاده از مدل های شناسایی شده و استفاده از تحلیل رگرسیون برای پیش بینی مدل یانگ داربست های استخوانی می‌توان روابط ساخته شده از جنس هیدروکسی آپاتیت را استخراج کرد.

𝐸 = −۱۰۹٫۴۶𝜙 + ۹۰٫۱۰۱

𝐸 = ۱۴۷٫۰۷𝜙۲ − ۲۵۶٫۵۳𝜙 + ۱۱۳٫۳۹

𝐸 = −۸۸٫۷۹۹𝜙۳ + ۲۸۰٫۲۷𝜙۲ − ۳۰۸٫۵۲𝜙 + ۱۱۷٫۱۸

𝜈 = −۰٫۰۵۴۳𝜙 + ۰٫۲۶۱

𝜈 = ۰٫۰۵۷𝜙۲ − ۰٫۱۱۱۳𝜙 + ۰٫۲۷

𝜈 = −۰٫۰۸۶𝜙۳ + ۰٫۰۸۴۸𝜙۲ − ۰٫۱۲۲۱𝜙 + ۰٫۲۷۰۸

بدیهی است که براساس مقادیر ارائه شده رگرسیون های درجه ۳(به دلیل بالاتر بودن مقدار ضرایب همبستگی) و تعیین آنها معادلات برازش مناسب تری برای تخمین مدل یانگ و ضریب پواسون است. از معادلات ارائه شده می‌توان برای تخمین سریع مقادیر مدل یانگ و ضریب پواسون داربست های استخوانی ساخته شده از جنس هیدروکسی آپاتیت استفاده کرد.