کشانده

در هندسه، کِشاندِه یا تراکتریکس (انگلیسی: Tractrix) یک منحنی ریاضی مسطح است که می‌توان آن را به عنوان مسیر حرکت یک سگ تصور کرد که با یک قلاده (به طول ثابت) صاحب خود را دنبال می‌کند، در حالی که صاحب سگ (بسیار) آهسته در یک خط مستقیم عمود بر جهت اولیه قلاده حرکت می‌کند.^[۱]

در شکل روبه‌رو، صاحب سگ (A) در ابتدا در مبدأ قرار دارد و سگ (P) با یک قلاده به طول AP روی محور y قرار دارد. صاحب سگ در امتداد محور x حرکت می‌کند.

این منحنی اولین بار توسط دانشمند فرانسوی کلود پرو در سال ۱۶۷۰ معرفی شد و بعداً توسط آیزاک نیوتن (۱۶۷۶) و کریستیان هویگنس (۱۶۹۳) مورد مطالعه قرار گرفت.^[۲]

تعریف

کشانده منحنیای است که یک جسم در امتداد آن، تحت تأثیر اصطکاک، حرکت می‌کند، هنگامی که توسط یک پاره‌خط متصل به یک نقطه کشنده (tractor) روی صفحه افقی کشیده می‌شود که با سرعت بی‌نهایت‌کوچک در زاویه قائمه نسبت به خط اولیه بین جسم و کشنده حرکت می‌کند؛ بنابراین، کشانده یک منحنی تعقیب است.

استخراج ریاضی

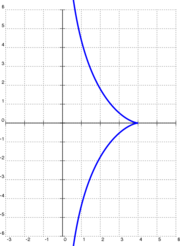
فرض کنید جسم در (a، ۰) (یا (۴٬۰) در مثال سمت راست) و کشنده در مبدأ (ریاضیات) قرار دارد، بنابراین a طول نخ کشنده است (۴ در مثال سمت راست). سپس کشنده شروع به حرکت در امتداد محور y در جهت مثبت می‌کند. در هر لحظه، نخ مماس بر منحنی ۱=y = y(x) خواهد بود که توسط جسم توصیف می‌شود، به طوری که کاملاً توسط حرکت کشنده تعیین می‌شود. از نظر ریاضی، اگر مختصات جسم (x, y) باشد، مختصات y کشنده با استفاده از قضیه فیثاغورس برابر است با $y+\operatorname {sign} (y){\sqrt {a^{2}-x^{2}}},$ . با نوشتن اینکه شیب نخ برابر با مماس بر منحنی است، به معادله دیفرانسیل زیر می‌رسیم:

{\frac {dy}{dx}}=\pm {\frac {\sqrt {a^{2}-x^{2}}}{x}}

با شرط اولیه ۱=y(a) = ۰‎. حل آن به صورت زیر است:

y=\int _{x}^{a}{\frac {\sqrt {a^{2}-t^{2}}}{t}}\,dt=\pm \!\left(a\ln {\frac {a+{\sqrt {a^{2}-x^{2}}}}{x}}-{\sqrt {a^{2}-x^{2}}}\right),

که در آن علامت $\pm$ به جهت (مثبت یا منفی) حرکت کشنده بستگی دارد.

جمله اول این راه حل را می‌توان به صورت زیر نیز نوشت:

a\operatorname {arsech} {\frac {x}{a}},

که در آن arsech تابع وارون هذلولوی است.

علامت قبل از حل به این بستگی دارد که کشنده به سمت بالا یا پایین حرکت کند. هر دو شاخه به کشانده تعلق دارند و در نقطه نقطه بازگشت (a، ۰) به هم می‌رسند.

پایه کشانده

کشانده ایجاد شده توسط انتهای یک میله (که صاف روی زمین قرار دارد). انتهای دیگر آن ابتدا هل داده می‌شود و سپس توسط یک انگشت کشیده می‌شود تا به یک طرف بچرخد.

ویژگی اساسی کشانده، ثابت بودن فاصله بین یک نقطه P روی منحنی و محل تقاطع مماس در P با مجانب منحنی است.

کشانده را می‌توان به روش‌های مختلفی در نظر گرفت:

این مکان هندسی مرکز یک مارپیچ هذلولی است که روی یک خط مستقیم می‌غلتد (بدون لغزش).
این گستران تابع زنجیره‌وار است که یک رشته کاملاً انعطاف‌پذیر، الاستومر و همگن متصل به دو نقطه را که تحت تأثیر یک میدان گرانش قرار دارد، توصیف می‌کند. زنجیره‌وار دارای معادله $y(x) = a cosh .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}x/a$ .
مسیری که توسط وسط محور عقب یک ماشین که با طناب با سرعت ثابت و با جهت ثابت (در ابتدا عمود بر وسیله نقلیه) کشیده می‌شود، تعیین می‌شود.
این یک منحنی (غیر خطی) است که یک دایره به شعاع a که روی یک خط مستقیم می‌غلتد، با مرکز آن در محور x، همیشه عمود بر آن تلاقی می‌کند.

تابع یک مجانب افقی می‌پذیرد. منحنی نسبت به محور y متقارن است. شعاع انحنا برابر است با $r = a cot x / y$ .

یک نتیجه مهم کشانده، مطالعه رویه دورانی آن حول مجانبش بود: شبه‌کره. این رویه که توسط یوجنیو بلترامی در سال ۱۸۶۸ مورد مطالعه قرار گرفت،^[۳] به عنوان یک سطح با خمیدگی گاوس ثابت منفی، یک مدل محلی از هندسه هذلولوی است. این ایده توسط کاسنر و نیومن در کتابشان «ریاضیات و تخیل» بیشتر پیش برده شد، جایی که آنها یک قطار اسباب‌بازی را نشان می‌دهند که یک ساعت جیبی را می‌کشد تا کشانده را تولید کند.^[۴]

ویژگی‌ها

این منحنی را می‌توان با معادله $x=t-\tanh(t),y=1/{\cosh(t)}$ پارامتری کرد.^[۵]
با توجه به روش هندسی که تعریف شد، کشانده این ویژگی را دارد که پاره خط مماس آن، بین مجانب و نقطه تماس، طول ثابت a دارد.
طول قوس یک شاخه بین $x = x 1$ و $x = x 2$ برابر است با $a ln x 1 / x 2$ .
مساحت بین کشانده و مجانب آن $π a 2 / 2$ , است که می‌توان آن را با استفاده از انتگرال یا قضیه مامیکون پیدا کرد.
منحنی محاطی نرمال (هندسه)‌های کشانده (یعنی گسترنده کشانده) زنجیره‌وار (یا منحنی زنجیری) است که توسط $y = a cosh x / a$ داده می‌شود.
رویه حاصل از دوران کشانده حول مجانبش یک شبه‌کره است.
کشانده یک منحنی متعالی است؛ نمی‌توان آن را با یک معادله چند جمله‌ای تعریف کرد.

کاربرد عملی

در سال ۱۹۲۷، P. G. A. H. Voigt یک طرح بلندگوی شیپوری را بر اساس این فرض ثبت اختراع کرد که موج صوتی که از طریق شیپور حرکت می‌کند، کروی با شعاع ثابت است. ایده این است که اعوجاج ناشی از انعکاس داخلی صدا در داخل شیپور به حداقل برسد. شکل حاصل، رویه دورانی یک کشانده است.^[۶]
یک کاربرد مهم در فناوری شکل‌دهی ورق‌های فلزی است. به‌طور خاص، یک پروفیل کشانده برای گوشه قالب استفاده می‌شود که در آن ورق فلز در طول کشش عمیق خم می‌شود.^[۷]

طراحی چرخ‌دنده تسمه‌دار-پولی با استفاده از شکل زنجیره‌وار کشانده برای دندانه‌های خود، کارایی بهبود یافته‌ای را برای انتقال قدرت مکانیکی فراهم می‌کند.^[۸] این شکل اصطکاک دندانه‌های تسمه درگیر با پولی را به حداقل می‌رساند، زیرا دندانه‌های متحرک با حداقل تماس لغزشی درگیر و جدا می‌شوند. طرح‌های اصلی تسمه تایمینگ از اشکال ساده‌تر دندانه‌های ذوزنقهای یا دایره‌ای استفاده می‌کردند که باعث لغزش و اصطکاک قابل توجهی می‌شدند.

دستگاه‌های رسم

در اکتبر تا نوامبر ۱۶۹۲، کریستین هویگنس سه ماشین طراحی کشانده را توصیف کرد.^[۹]
در سال ۱۶۹۳ گوتفریت لایبنیتس یک «ماشین کششی جهانی» ابداع کرد که از نظر تئوری می‌توانست هر معادله دیفرانسیل معمولی را ادغام کند.^[۱۰] این مفهوم یک سازوکار محاسباتی آنالوگ بود که اصل کششی را پیاده‌سازی می‌کرد. ساخت دستگاه با فناوری زمان لایب‌نیتس غیرعملی بود و هرگز محقق نشد.
در سال ۱۷۰۶ جان پرکس یک دستگاه کششی برای تحقق یکپارچگی تابع هذلولوی ساخت.^[۱۱]
در سال ۱۷۲۹ جووانی پولنی یک دستگاه کششی ساخت که امکان رسم لگاریتم‌ها را فراهم می‌کرد.^[۱۲]

تاریخچه همه این ماشین‌ها را می‌توان در مقاله‌ای از هنک بوس مشاهده کرد.^[۹]

جستارهای وابسته

سطح دینی
تابع هذلولوی برای tanh, sech, csch, arcosh
لگاریتم طبیعی برای ln
تابع علامت برای sgn
توابع مثلثاتی برای sin, cos, tan, arccot, csc

منابع

↑ Wikipedia-bijdragers, "Tractrix," Wikipedia, de vrije encyclopedie, https://nl.wikipedia.org/w/index.php?title=Tractrix&oldid=46166907 (accessed juli 19, 2024).
↑ Stillwell, John (2010). [[۱](https://books.google.com/books?id=V7mxZqjs5yUC) Mathematics and Its History] (revised, 3rd ed.). Springer Science & Business Media. p. 345. ISBN 978-1-4419-6052-8. {{cite book}}: Check |url= value (help), [[۲](https://books.google.com/books?id=V7mxZqjs5yUC&pg=PA345) extract of page 345]
↑ Beltrami, E. (1868). "Saggio di interpretazione della geometria non euclidea". Giornale di Matematiche. 6: 284. As cited by Bertotti, Bruno; Catenacci, Roberto; Dappiaggi, Claudio (2007). "Pseudospheres in geometry and physics: from Beltrami to de Sitter and beyond". A great mathematician of the nineteenth century. Papers in honor of Eugenio Beltrami (1835–1900) (Italian). Ist. Lombardo Accad. Sci. Lett. Incontr. Studio. Vol. 39. LED–Ed. Univ. Lett. Econ. Diritto, Milan. pp. 165–194. arXiv:math/0506395. ISBN 978-88-7916-359-0. MR 2374676.
↑ Kasner, Edward; Newman, James (2013). [[۳](https://books.google.com/books?id=-bXDAgAAQBAJ&pg=PA141) "Figure 45(a)"]. Mathematics and the Imagination. Dover Books on Mathematics. Courier Corporation. p. 141. ISBN 978-0-486-32027-4. {{cite book}}: Check |contribution-url= value (help)
↑ O'Connor, John J.; Robertson, Edmund F., "Tractrix", MacTutor History of Mathematics archive, University of St Andrews
↑ [[۴](http://www.volvotreter.de/downloads/Dinsdale_Horns_1.pdf)^{^{[پیوند مرده]}} Horn loudspeaker design pp. 4–5. (Reprinted from Wireless World, March 1974)]
↑ Lange, Kurt (1985). Handbook of Metal Forming. McGraw Hill Book Company. p. 20.43.
↑ [[۵](https://www.gates.com/~/media/files/gates/industrial/power-transmission/manuals/powergripdrivedesignmanual_17195_2014.pdf) "Gates Powergrip GT3 Drive Design Manual"]. Gates Corporation. 2014. p. 177. Retrieved 17 November 2017. The GT tooth profile is based on the tractix mathematical function. Engineering handbooks describe this function as a “frictionless” system. This early development by Schiele is described as an involute form of a catenary. {{cite web}}: Check |url= value (help)^{^{[پیوند مرده]}}
↑ ^۹٫۰ ^۹٫۱ Bos, H. J. M. (1989). [[۶](http://www.gewina.nl/journals/tractrix/bos89.pdf) "Recognition and Wonder – Huygens, Tractional Motion and Some Thoughts on the History of Mathematics"]. Euclides. 63: 65–76. {{cite journal}}: Check |url= value (help)^{^{[پیوند مرده]}}
↑ Milici, Pietro (2014). Lolli, Gabriele (ed.). From Logic to Practice: Italian Studies in the Philosophy of Mathematics. Springer. ... mechanical devices studied … to solve particular differential equations … We must recollect Leibniz's 'universal tractional machine'
↑ Perks, John (1706). "The construction and properties of a new quadratrix to the hyperbola". Philosophical Transactions. 25: 2253–2262. doi:10.1098/rstl.1706.0017. JSTOR 102681. S2CID 186211499.
↑ Poleni, John (1729). Epistolarum mathematicanim fasciculus. p. letter no. 7.

مشارکت‌کنندگان ویکی‌پدیا. «Tractrix». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۱۹ ژوئیه ۲۰۲۴.

پیوند به بیرون

[1] Wikipedia-bijdragers, "Tractrix," Wikipedia, de vrije encyclopedie, https://nl.wikipedia.org/w/index.php?title=Tractrix&oldid=46166907 (accessed juli 19, 2024).

[2] Stillwell, John (2010). [[۱](https://books.google.com/books?id=V7mxZqjs5yUC) Mathematics and Its History] (revised, 3rd ed.). Springer Science & Business Media. p. 345. ISBN 978-1-4419-6052-8. {{cite book}}: Check |url= value (help), [[۲](https://books.google.com/books?id=V7mxZqjs5yUC&pg=PA345) extract of page 345]

[3] Beltrami, E. (1868). "Saggio di interpretazione della geometria non euclidea". Giornale di Matematiche. 6: 284. As cited by Bertotti, Bruno; Catenacci, Roberto; Dappiaggi, Claudio (2007). "Pseudospheres in geometry and physics: from Beltrami to de Sitter and beyond". A great mathematician of the nineteenth century. Papers in honor of Eugenio Beltrami (1835–1900) (Italian). Ist. Lombardo Accad. Sci. Lett. Incontr. Studio. Vol. 39. LED–Ed. Univ. Lett. Econ. Diritto, Milan. pp. 165–194. arXiv:math/0506395. ISBN 978-88-7916-359-0. MR 2374676.

[4] Kasner, Edward; Newman, James (2013). [[۳](https://books.google.com/books?id=-bXDAgAAQBAJ&pg=PA141) "Figure 45(a)"]. Mathematics and the Imagination. Dover Books on Mathematics. Courier Corporation. p. 141. ISBN 978-0-486-32027-4. {{cite book}}: Check |contribution-url= value (help)

[5] O'Connor, John J.; Robertson, Edmund F., "Tractrix", MacTutor History of Mathematics archive, University of St Andrews

[6] [[۴](http://www.volvotreter.de/downloads/Dinsdale_Horns_1.pdf)^{^{[پیوند مرده]}} Horn loudspeaker design pp. 4–5. (Reprinted from Wireless World, March 1974)]

[7] Lange, Kurt (1985). Handbook of Metal Forming. McGraw Hill Book Company. p. 20.43.

[8] [[۵](https://www.gates.com/~/media/files/gates/industrial/power-transmission/manuals/powergripdrivedesignmanual_17195_2014.pdf) "Gates Powergrip GT3 Drive Design Manual"]. Gates Corporation. 2014. p. 177. Retrieved 17 November 2017. The GT tooth profile is based on the tractix mathematical function. Engineering handbooks describe this function as a “frictionless” system. This early development by Schiele is described as an involute form of a catenary. {{cite web}}: Check |url= value (help)^{^{[پیوند مرده]}}

[bos-9] ۹٫۰ ^۹٫۱ Bos, H. J. M. (1989). [[۶](http://www.gewina.nl/journals/tractrix/bos89.pdf) "Recognition and Wonder – Huygens, Tractional Motion and Some Thoughts on the History of Mathematics"]. Euclides. 63: 65–76. {{cite journal}}: Check |url= value (help)^{^{[پیوند مرده]}}

[10] Milici, Pietro (2014). Lolli, Gabriele (ed.). From Logic to Practice: Italian Studies in the Philosophy of Mathematics. Springer. ... mechanical devices studied … to solve particular differential equations … We must recollect Leibniz's 'universal tractional machine'

[11] Perks, John (1706). "The construction and properties of a new quadratrix to the hyperbola". Philosophical Transactions. 25: 2253–2262. doi:10.1098/rstl.1706.0017. JSTOR 102681. S2CID 186211499.

[12] Poleni, John (1729). Epistolarum mathematicanim fasciculus. p. letter no. 7.

[۱]

[۲]

[۳]

[۴]

[۵]

[۶]

[۷]

[۸]

[۹]

[۱۰]

[۱۱]

[۱۲]