در زمینه ریاضی آنالیز عددی ، الگوریتم De Casteljau یک روش بازگشتی برای ارزیابی چند جمله ای ها در فرم برنشتاین یا منحنی های Bézier است که به نام مخترع آن Paul de Casteljau نامگذاری شده است. از الگوریتم De Casteljau می توان برای تقسیم منحنی بزیر به دو منحنی بزیر در مقدار پارامتر دلخواه استفاده کرد.
اگرچه الگوریتم در مقایسه با رویکرد مستقیم برای بیشتر معماری ها کندتر است ، اما از نظر عددی پایدارتر است .
منحنی Bézier B (درجه n ، با نقاط کنترل)
β
0
,
…
,
β
n
{\displaystyle \beta _{0},\ldots ,\beta _{n}}
B
(
t
)
=
∑
i
=
0
n
β
i
b
i
,
n
(
t
)
{\displaystyle B(t)=\sum _{i=0}^{n}\beta _{i}b_{i,n}(t)}
جایی که b یک چند جمله ای مبتنی برنشتاین است
b
i
,
n
(
t
)
=
(
n
i
)
(
1
−
t
)
n
−
i
t
i
{\displaystyle b_{i,n}(t)={n \choose i}(1-t)^{n-i}t^{i}}
منحنی در نقطه t 0 را می توان با رابطه بازگشتی ارزیابی کرد
β
i
(
0
)
:=
β
i
,
i
=
0
,
…
,
n
{\displaystyle \beta _{i}^{(0)}:=\beta _{i}{\mbox{, }}i=0,\ldots ,n}
β
i
(
j
)
:=
β
i
(
j
−
1
)
(
1
−
t
0
)
+
β
i
+
1
(
j
−
1
)
t
0
,
i
=
0
,
…
,
n
−
j
,
j
=
1
,
…
,
n
{\displaystyle \beta _{i}^{(j)}:=\beta _{i}^{(j-1)}(1-t_{0})+\beta _{i+1}^{(j-1)}t_{0}{\mbox{, }}i=0,\ldots ,n-j{\mbox{, }}j=1,\ldots ,n}
سپس ، ارزیابی از
B
{\displaystyle B}
t
0
{\displaystyle t_{0}}
(
n
2
)
{\displaystyle {\binom {n}{2}}}
B
(
t
0
)
{\displaystyle B(t_{0})}
B
(
t
0
)
=
β
0
(
n
)
.
{\displaystyle B(t_{0})=\beta _{0}^{(n)}.}
علاوه بر این ، منحنی بزیر
B
{\displaystyle B}
t
0
{\displaystyle t_{0}}
β
0
(
0
)
,
β
0
(
1
)
,
…
,
β
0
(
n
)
{\displaystyle \beta _{0}^{(0)},\beta _{0}^{(1)},\ldots ,\beta _{0}^{(n)}}
β
0
(
n
)
,
β
1
(
n
−
1
)
,
…
,
β
n
(
0
)
{\displaystyle \beta _{0}^{(n)},\beta _{1}^{(n-1)},\ldots ,\beta _{n}^{(0)}}
در اینجا مثالی از پیاده سازی الگوریتم De Casteljau در هاسکل آورده شده است :
deCasteljau :: Double -> [( Double , Double )] -> ( Double , Double )
deCasteljau t [ b ] = b
deCasteljau t coefs = deCasteljau t reduced
where
reduced = zipWith ( lerpP t ) coefs ( tail coefs )
lerpP t ( x0 , y0 ) ( x1 , y1 ) = ( lerp t x0 x1 , lerp t y0 y1 )
lerp t a b = t * b + ( 1 - t ) * a
هنگام انجام محاسبه با دست ، مفید است که ضرایب را در یک طرح مثلث به صورت زیر بنویسید:
β
0
=
β
0
(
0
)
β
0
(
1
)
β
1
=
β
1
(
0
)
⋱
⋮
⋮
β
0
(
n
)
β
n
−
1
=
β
n
−
1
(
0
)
β
n
−
1
(
1
)
β
n
=
β
n
(
0
)
{\displaystyle {\begin{matrix}\beta _{0}&=\beta _{0}^{(0)}&&&\\&&\beta _{0}^{(1)}&&\\\beta _{1}&=\beta _{1}^{(0)}&&&\\&&&\ddots &\\\vdots &&\vdots &&\beta _{0}^{(n)}\\&&&&\\\beta _{n-1}&=\beta _{n-1}^{(0)}&&&\\&&\beta _{n-1}^{(1)}&&\\\beta _{n}&=\beta _{n}^{(0)}&&&\\\end{matrix}}}
هنگام انتخاب نقطه t 0 برای ارزیابی چند جمله ای برنشتاین می توان از دو مورب طرح مثلث برای ساخت تقسیم چند جمله ای استفاده کرد
B
(
t
)
=
∑
i
=
0
n
β
i
(
0
)
b
i
,
n
(
t
)
,
t
∈
[
0
,
1
]
{\displaystyle B(t)=\sum _{i=0}^{n}\beta _{i}^{(0)}b_{i,n}(t){\mbox{, }}\qquad t\in [0,1]}
به
B
1
(
t
)
=
∑
i
=
0
n
β
0
(
i
)
b
i
,
n
(
t
t
0
)
,
t
∈
[
0
,
t
0
]
{\displaystyle B_{1}(t)=\sum _{i=0}^{n}\beta _{0}^{(i)}b_{i,n}\left({\frac {t}{t_{0}}}\right){\mbox{, }}\qquad t\in [0,t_{0}]}
و
B
2
(
t
)
=
∑
i
=
0
n
β
i
(
n
−
i
)
b
i
,
n
(
t
−
t
0
1
−
t
0
)
,
t
∈
[
t
0
,
1
]
{\displaystyle B_{2}(t)=\sum _{i=0}^{n}\beta _{i}^{(n-i)}b_{i,n}\left({\frac {t-t_{0}}{1-t_{0}}}\right){\mbox{, }}\qquad t\in [t_{0},1]}
ما می خواهیم چند جمله ای برنشتاین درجه 2 را با ضرایب برنشتاین ارزیابی کنیم
β
0
(
0
)
=
β
0
{\displaystyle \beta _{0}^{(0)}=\beta _{0}}
β
1
(
0
)
=
β
1
{\displaystyle \beta _{1}^{(0)}=\beta _{1}}
β
2
(
0
)
=
β
2
{\displaystyle \beta _{2}^{(0)}=\beta _{2}}
در نقطه t 0 .
بازگشت را با عبارات زیر شروع می کنیم
β
0
(
1
)
=
β
0
(
0
)
(
1
−
t
0
)
+
β
1
(
0
)
t
0
=
β
0
(
1
−
t
0
)
+
β
1
t
0
{\displaystyle \beta _{0}^{(1)}=\beta _{0}^{(0)}(1-t_{0})+\beta _{1}^{(0)}t_{0}=\beta _{0}(1-t_{0})+\beta _{1}t_{0}}
β
1
(
1
)
=
β
1
(
0
)
(
1
−
t
0
)
+
β
2
(
0
)
t
0
=
β
1
(
1
−
t
0
)
+
β
2
t
0
{\displaystyle \beta _{1}^{(1)}=\beta _{1}^{(0)}(1-t_{0})+\beta _{2}^{(0)}t_{0}=\beta _{1}(1-t_{0})+\beta _{2}t_{0}}
و با تکرار دوم بازگشت متوقف می شود با:
β
0
(
2
)
=
β
0
(
1
)
(
1
−
t
0
)
+
β
1
(
1
)
t
0
=
β
0
(
1
−
t
0
)
(
1
−
t
0
)
+
β
1
t
0
(
1
−
t
0
)
+
β
1
(
1
−
t
0
)
t
0
+
β
2
t
0
t
0
=
β
0
(
1
−
t
0
)
2
+
β
1
2
t
0
(
1
−
t
0
)
+
β
2
t
0
2
{\displaystyle {\begin{aligned}\beta _{0}^{(2)}&=\beta _{0}^{(1)}(1-t_{0})+\beta _{1}^{(1)}t_{0}\\\ &=\beta _{0}(1-t_{0})(1-t_{0})+\beta _{1}t_{0}(1-t_{0})+\beta _{1}(1-t_{0})t_{0}+\beta _{2}t_{0}t_{0}\\\ &=\beta _{0}(1-t_{0})^{2}+\beta _{1}2t_{0}(1-t_{0})+\beta _{2}t_{0}^{2}\end{aligned}}}
که انتظار می رود چند جمله ای درجه 2 برنشتاین باشد
منحنی Bézier هنگام ارزیابی منحنی بزیر از درجه n در فضای 3 بعدی با
n
+
1
{\displaystyle n+1}
P i
B
(
t
)
=
∑
i
=
0
n
P
i
b
i
,
n
(
t
)
,
t
∈
[
0
,
1
]
{\displaystyle \mathbf {B} (t)=\sum _{i=0}^{n}\mathbf {P} _{i}b_{i,n}(t){\mbox{, }}t\in [0,1]}
با
P
i
:=
(
x
i
y
i
z
i
)
{\displaystyle \mathbf {P} _{i}:={\begin{pmatrix}x_{i}\\y_{i}\\z_{i}\end{pmatrix}}}
منحنی بزیر را به سه معادله جداگانه تقسیم می کنیم
B
1
(
t
)
=
∑
i
=
0
n
x
i
b
i
,
n
(
t
)
,
t
∈
[
0
,
1
]
{\displaystyle B_{1}(t)=\sum _{i=0}^{n}x_{i}b_{i,n}(t){\mbox{, }}t\in [0,1]}
B
2
(
t
)
=
∑
i
=
0
n
y
i
b
i
,
n
(
t
)
,
t
∈
[
0
,
1
]
{\displaystyle B_{2}(t)=\sum _{i=0}^{n}y_{i}b_{i,n}(t){\mbox{, }}t\in [0,1]}
B
3
(
t
)
=
∑
i
=
0
n
z
i
b
i
,
n
(
t
)
,
t
∈
[
0
,
1
]
{\displaystyle B_{3}(t)=\sum _{i=0}^{n}z_{i}b_{i,n}(t){\mbox{, }}t\in [0,1]}
که ما به صورت جداگانه با استفاده از الگوریتم De Casteljau ارزیابی می کنیم.
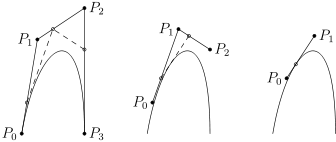
تفسیر هندسی الگوریتم De Casteljau ساده است.
یک منحنی بزیر با نقاط کنترل را در نظر بگیرید
P
0
,
.
.
.
,
P
n
{\displaystyle \scriptstyle P_{0},...,P_{n}}
اکنون هر بخش خط از این چند ضلعی را با نسبت تقسیم کنید
t
:
(
1
−
t
)
{\displaystyle \scriptstyle t:(1-t)}
این فرآیند را تا رسیدن به نقطه واحد تکرار کنید - این نقطه منحنی مربوط به پارامتر است
t
{\displaystyle \scriptstyle t}
تصویر زیر این روند را برای یک منحنی مکعب بزیر نشان می دهد:
توجه داشته باشید که نقاط میانی که ساخته شده اند در واقع نقاط کنترل دو منحنی جدید بزیر هستند ، هر دو دقیقاً با یک منحنی قدیمی مطابقت دارند. این الگوریتم نه تنها منحنی را در ارزیابی می کند
t
{\displaystyle \scriptstyle t}
t
{\displaystyle \scriptstyle t}
تفسیری که در بالا ارائه شد برای یک منحنی غیر منطقی بزیر معتبر است. برای ارزیابی منحنی بیزیر منطقی در
R
n
{\displaystyle \scriptstyle \mathbf {R} ^{n}}
R
n
+
1
{\displaystyle \scriptstyle \mathbf {R} ^{n+1}}
{
(
x
i
,
y
i
,
z
i
)
}
{\displaystyle \scriptstyle \{(x_{i},y_{i},z_{i})\}}
{
w
i
}
{\displaystyle \scriptstyle \{w_{i}\}}
{
(
w
i
x
i
,
w
i
y
i
,
w
i
z
i
,
w
i
)
}
{\displaystyle \scriptstyle \{(w_{i}x_{i},w_{i}y_{i},w_{i}z_{i},w_{i})\}}
R
4
{\displaystyle \scriptstyle \mathbf {R} ^{4}}
به طور کلی ، عملیات روی یک منحنی منطقی (یا سطح) معادل عملیات روی یک منحنی غیر منطقی در یک فضای فرافکنی است . این بازنمایی به عنوان "نقاط کنترل وزنی" و وزن اغلب هنگام ارزیابی منحنی های منطقی راحت است.
Farin, Gerald & Hansford, Dianne (2000). The Essentials of CAGD . Natic, MA: A K Peters, Ltd. شابک ۱−۵۶۸۸۱−۱۲۳−۳ تقریب خطی منحنی های Bézier - شرح الگوریتم De Casteljau ، از جمله یک معیار برای تعیین زمان متوقف کردن جمع کردن [ <span title="similar to recussion (November 2019)">بررسی املا</span> ] منحنی های Bezier و Picasso - شرح و تصویر الگوریتم De Casteljau اعمال شده در منحنی های Bézier مکعب.














![{\displaystyle B(t)=\sum _{i=0}^{n}\beta _{i}^{(0)}b_{i,n}(t){\mbox{, }}\qquad t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e77c39da52ed389bc7312f1ad63533686f9c9d4)
![{\displaystyle B_{1}(t)=\sum _{i=0}^{n}\beta _{0}^{(i)}b_{i,n}\left({\frac {t}{t_{0}}}\right){\mbox{, }}\qquad t\in [0,t_{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e7c0564c2e617cc2f2f6e5b1431f6c0f5ef7eb0)
![{\displaystyle B_{2}(t)=\sum _{i=0}^{n}\beta _{i}^{(n-i)}b_{i,n}\left({\frac {t-t_{0}}{1-t_{0}}}\right){\mbox{, }}\qquad t\in [t_{0},1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c7b65302aae69518c00a19f8bb4e039066f01fd)







![{\displaystyle \mathbf {B} (t)=\sum _{i=0}^{n}\mathbf {P} _{i}b_{i,n}(t){\mbox{, }}t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d2672593e125903fae4edbc4d5d35bbe746d45b)

![{\displaystyle B_{1}(t)=\sum _{i=0}^{n}x_{i}b_{i,n}(t){\mbox{, }}t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8b791f72b3ab68affda225c96a9f6a182c99e1e)
![{\displaystyle B_{2}(t)=\sum _{i=0}^{n}y_{i}b_{i,n}(t){\mbox{, }}t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8522e2e41255cee69b83f7b5d1a617bf15cc9129)
![{\displaystyle B_{3}(t)=\sum _{i=0}^{n}z_{i}b_{i,n}(t){\mbox{, }}t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7dbfae0e2cbda9c867f5b518fd506b3e8287b30e)