هزینه پایداری

در نظریه بازی‌ها، هزینه پایداری (به انگلیسی: price of stability یا PoS) یک بازی به نسبت "بهترین هزینه اجتماعی تعادل‌های نش بازی" به "هزینهٔ اجتماعی حالت بهینه اجتماعی" گفته می‌شود. هدف از تعریف این نسبت پی بردن به این موضوع است که در یک بازی دخالت یک قدرت سوم برای خارج کردن رفتار بازیکنان از "خودخواه محض" بودن، به چه اندازه سودمند است. در کتاب دنیای جدید شجاع اثر آلدوس هاکسلی (Aldous Huxley) نیز اشاره‌ای به این مفهوم شده‌است. همچنین هنگامی که ما می‌خواهیم خوب و مؤثر بودن یک تعادل نش را در یک بازی خاص اندازه بگیریم، غالباً دربارهٔ هزینه آشوب (PoA) حرف می‌زنیم.

تعاریف اولیه

در یک بازی مفروض G با مجموعهٔ بازیکنان P و مجموعهٔ استراتژی‌های S، اگر {E:S^|P| -> {0,1 یک تابع تعادل بوده و f یک تابع هدف باشد که معمولاً سودمحور (به صورت جمع سودهای بازیکنان) یا بیشینه‌محور (به صورت بیشترین مقدار سود یک بازیکن) تعریف می‌شود، آنگاه اگر S1 تا Sn مجموعهٔ همهٔ استراتژی پروفایل‌های تعادل باشند، منظور از هزینهٔ پایداری نسبت ((f(S_i))/(f(S) است که در آن S_i تعادلی است که مقدار f را در میان سایر S_jها بیشینه می‌کند و S استراتژی پروفایلی است که مقدار f را بین همهٔ استراتژی پروفایل‌ها بیشینه می‌کند.

در کنار هزینهٔ پایداری، معیار دیگری نیز با عنوان هزینهٔ آشوب تعریف می‌شود که به معنی نسبت بدترین تعادل به حالت بهینهٔ تابع است.

به عبارتی هزینهٔ پایداری و هزینهٔ آشوب به همراه هم نشان می‌دهند اگر یک قدرت خارج از بازیکنان، آن‌ها را با قرار دادن سیاست‌هایی مجبور به انجام یکی دیگر از تعادلها کند، مقدار سود چقدر خواهد بود و اگر این کار را نکنند مقدار ضرر چقدر خواهد شد و در نهایت مشخص می‌شود که آیا این کار به صرفه هست یا نه. به‌طور خاص، هزینهٔ پایداری وقتی کاربردی است که بازیکنان برای دستیابی به یک حالت بهینه حاضر به همکاری هستند و مثالی خوب از هزینهٔ آشوب در اینترنت است که هر شرکت بدون در نظر گرفتن نفع جهانی در پی بیشینه کردن سود خود است.

مثال‌ها

همانگونه که گفته‌شد هزینه پایداری برابر است با بیشترین مقدار هزینهٔ اجتماعی تعادل‌های نش بازی تقسیم بر هزینهٔ اجتماعی در حالت بهینهٔ اجتماعی.

برای مثال در بازی معمای زندانی‌های زیر، تنها یک تعادل نش وجود دارد که عبارت است از (عدم‌همکاری، عدم‌همکاری) بنابراین داریم: هزینه پایداری = هزینه بی‌نظمی = ۱/۲.

استراتژی‌ها	همکاری	عدم‌همکاری
همکاری	۲، ۲	۰، ۳
عدم‌همکاری	۳، ۰	۱، ۱

اما در مثال زیر که در واقع نسخه‌ای از بازی نبرد دو جنس است، دو تعادل وجود دارد: (A,A) و (R,R) با هزینهٔ اجتماعی ۳ و ۱۵. بنابراین در این بازی مقدار سود اجماعی حالت بهینهٔ اجتماعی ۱۵. بنابراین مقدار هزینه پایداری ۱ خواهد بود و هزینه بی‌نظمی ۱/۱۵.

استراتژی‌ها	A	R
A	۲، ۱	۰، ۰
R	۰، ۰	۵، ۱۰

پیشینه و تاریخ‌شمار

هزینه پایداری نخستین بار توسط آ. شولتزان و م. موزز مورد مطالعه‌ای قرار گرفت که به مطالعات اِ. آنشلویچ مشهور است. آنها نشان دادند که همواره یک تعادل نش خالص در یک بازی وجود دارد و هزینه پایداری یک بازی حداکثر برابر n-اُمین عدد هارمونیک در یک گراف جهتدار است. برای یک گراف بدون جهت آنشلویچ و دیگران نشان دادند یک کران بالای ۴/۳ برای هزینه پایداری در یک گراف با یک منبع و با دو بازیکن وجود دارد. ژیان لی ثابت‌کرده‌است که برای یک گراف بدون‌جهت با یک مقصد مشخص که همهٔ بازیکنان باید به آن متصل شوند، هزینه پایداری این شبکهٔ بازی $O(\log n/\log \log n)$ است که n تعداد بازیکنان است. از طرفی دیگر هزینه بی‌نظمی نیز در این بازی حدود n است.

همچنین در تحقیقی دیگر که توسط آنشلویچ و جمعی دیگر از اعضای دپارتمان علوم کامپیوتر دانشگاه کرنل صورت پذیرفته‌است، نشان داده می‌شود که در یک طراحی شبکه‌ای با تخصیص هزینه عادلانه مقدار هزینه پایداری $O(\log n)$ می‌باشد.

بازی‌های طراحی شبکه

مدل شبکه‌ای ساده پیگو

میزان غیربهینگی تعادل‌ها در بازیها در حالت کلی قابل تخمین زدن نیست، این امر در بازی‌های ساده‌ای نظیر معمای زندانی‌ها هم قابل رویت است که تعادل در آن می‌تواند تا حد دلخواه غیر بهینه اجتماعی باشد. به همین منظور این فکر ایجاد شد تا به دنبال دسته‌هایی از بازیها بگردیم که در آنها تعادل بهینه به مقدار بهینه اجتماعی تا حد قابل قبولی نزدیک باشد. بازی‌های طراحی شبکه از این دسته اند.

مثال روبرو که با عنوان مثال پیگو (Pigou) به نام اقتصاددان پیگو در سال ۱۹۲۰ بیان شد، نشانگر یک مدل شبکه‌ای ساده است. در این مدل تعداد n بازیکن قصد رفتن از مبدأ s به مقصد t را دارند و برای این کار اگر مسیر بالایی را برگزینند یک واحد زمانی هزینه می‌کنند و اگر مسیر پایینی را برگزینند، به ازای هر واحد ترافیکی که از پایین می‌گذرد (که ممکن است نسبتی از کل جمعیت بازیکنان مثلاً ۰٫۱ آن باشد) یک واحد زمانی برای رسیدن به مقصد هزینه خواهند کرد. در این مثال اگر یک واحد ترافیک را کل افراد ایجاد کنند، حالت بهینهٔ اجتماعی زمانی اتفاق می‌افتد که نصف افراد از مسیر بالا و نصف دیگر از مسیر پایین عبور کنند و یک تعادل زمانی است که همهٔ افراد مسیر دوم را انتخاب کنند. در این مثال هم مقدار هزینهٔ آشوب و هم پایداری برابر با ۴/۳ خواهد بود. همچنین اگر شبکه به صورت گرافی جهت دار بزرگ شود اما همچنان تابع هزینهٔ هر مسیر به صورت ax+b باقی بماند، مقدار هزینه پایداری و آشوب حداکثر همین ۴/۳ خواهد بود.

این مثالی بسیار ساده از بازی‌های طراحی شبکه بود، در مثال‌های کلی‌تر به عنوان نمونه افراد این قابلیت را دارند که مبدأ و مقصدهای گوناگون داشته باشند. اما ویژگی‌ای ثابت در تمام چنین بازی‌هایی وجود دارد و آن این است که در تمام این بازی‌ها مقدار هزینهٔ آشوب با مقدار هزینهٔ پایداری یکسان است. این موضوع با استفاده از مفهوم تابع پتانسیل قابل اثبات است.

یک طراحی شبکه‌ای بازی باهزینه بی‌نظمی $\Omega (n)$

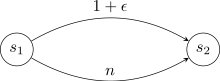
مثال دیگری از چنین بازی‌هایی، بازی طراحی شبکهٔ شپلی (Shapley) است. در این بازی یک گراف جهتدار وجود دارد که هر یال e آن دارای هزینهٔ ثابت 𝑐𝑒 می‌باشد. n بازیکن هر یک دارای مقصد و مبدأ خاص خود است و هدفش رسیدن از مقصد به مبدأ می‌باشد. مجموعهٔ استراتژی‌های هر فرد همهٔ مسیرهایی می‌باشد که آن فرد می‌تواند با آنها به مقصد برسد. در نهایت هزینهٔ هر فرد به این صورت مشخص می‌شود که به ازای هر یالی از گراف که در مسیر طی شده توسط او وجود دارد، هزینهٔ آن یال بین تمام کسانی که در استراتژیشان از آن مسیر عبور می‌کنند، به صورت مساوی تقسیم می‌شود. حال می‌خواهیم در این بازی میزان بهینگی تعادل نش را بسنجیم. به این منظور حالت ساده شده‌ای از این بازی مانند زیر را در نظر می‌گیریم.

در اینجا n بازیکن با مبدأ و مقصد یکسان s و t داریم و n و 1+e به ترتیب میزان هزینهٔ هریک از مسیرها هستند که در آن: e> 0. در این بازی حالتی که همهٔ افراد مسیر پایینی را انتخاب کنند، یک تعادل و حالتی که همگی مسیر بالایی را انتخاب کنند هم یک تعادل است و حالت بهینهٔ اجتماعی در حالت اول اتفاق می‌افتد. پس در اینجا میزان هزینهٔ پایداری برابر ۱ و میزان هزینهی آشوب برابر n است. البته در همهٔ بازی‌های شیپلی مقدار هزینهٔ پایداری برابر ۱ باقی نمی‌ماند.

آماده‌سازی

طراحی شبکه‌ای بازی‌ها بسیار برای هزینه پایداری مفید است. در این بازی‌ها، هزینه بی‌نظمی می‌تواند بدتر از هزینه پایداری باشد.

بازی زیر را در نظر بگیرید.

• n بازیکن؛
• هر بازیکن i قصد دارد که $s_{i}$ را به $t_{i}$ در یک گراف جهتدار $G=(V,E)$ وصل کند؛
• استراتژی‌های $P_{i}$ برای یک بازیکن عبارت‌اند از تمام مسیرهای از $s_{i}$ به $t_{i}$ در $G$؛
• هر یال یک هزینهٔ $c_{i}$؛
• "تخصیص هزینه عادلانه": هنگامی که $n_{e}$ بازیکن یال $e$ را انتخاب می‌کنند، هزینهٔ $\textstyle d_{e}(n_{e})={\frac {c_{e}}{n_{e}}}$ به‌طور مساوی بین آنها تقسیم می‌شود؛
• هزینه هر بازیکن برابر است با: $\textstyle C_{i}(S)=\sum _{e\in P_{i}}{\frac {c_{e}}{n_{e}}}$
• هزینه اجتماعی عبارت است از مجموع سودهای بازیکنان: $\textstyle SC(S)=\sum _{i}C_{i}(S)=\sum _{e\in S}n_{e}{\frac {c_{e}}{n_{e}}}=\sum _{e\in S}c_{e}$.

هزینه بی‌نظمی

هزینه بی‌نظمی می‌تواند $\Omega (n)$ باشد. طراحی شبکه‌ای بازی شیپلی را که در بالا گفته شد، در نظر بگیرید: دو تعادل متفاوت در این بازی وجود دارد؛ اگر همه یال $1+\varepsilon$ به اشتراک بگذارند، هزینهٔ اجتماعی برابر $1+\varepsilon$ خواهد بود. این تعادل در واقع یک هزینهٔ اجتماعی بهینه است. دقت کنید این که همه یال $n$ را به اشتراک بگذارند، نیز، یک تعادل نش است و تغییر به یال دیگر، هزینهٔ فرد موردنظر را افزایش می‌دهد.

بازی آسیب‌شناختی هزینه پایداری

کران پایین هزینه پایداری

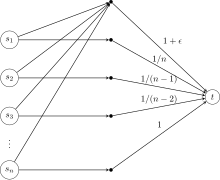
در اینجا یک بازی آسیب‌شناختی با محتوای مشابه برای هزینه پایداری داریم. در نظر بگیرید $n$ بازیکن، هر کدام از $s_{i}$ شروع می‌کنند و سعی در متصل شدن به $t$ دارند. هزینه یال برچسب‌گذاری‌نشده صفر در نظر گرفته می‌شود.

استراتژی بهینهٔ اجتماعی برای هر کس این است که یال $1+\varepsilon$ را به اشتراک بگذارد تا هزینهٔ اجتماعی $1+\varepsilon$ به دست آید. هرچند، تنها یک تعادل نش برای این بازی وجود دارد. باید توجه شود که در حالت بهینهٔ اجتماعی، هر بازیکن هزینهٔ $\textstyle {\frac {1+\varepsilon }{n}}$ می‌پردازد و بازیکن ۱ می‌تواند هزینه‌اش را با تغییر مسیر به یال $\textstyle {\frac {1}{n}}$ کاهش‌دهد. وقتی این اتفاق بیفتد، بازیکن ۲ نیز تمایل دارد یال $\textstyle {\frac {1}{n-1}}$ تغییر مسیر دهد و این روند به این شکل ادامه پیدا خواهد کرد. نهایتاً بازیکنان به تعادل نش برای یال خودشان خواهند رسید. این تخصیص هزینهٔ اجتماعی $\textstyle 1+{\frac {1}{2}}+\cdots +{\frac {1}{n}}=H_{n}$ خواهد داشت که $H_{n}$، $H_{n}$اُمین عدد هارمونیک خواهد بود؛ که برابر است با: $\Theta (\log n)$. بناباین با این که کران نخواهد داشت، هزینه پایداری در این بازی به‌طور نمایی بهتر از هزینه بی‌نظمی است.

کران بالای هزینه پایداری

باید دقت شود که بازی‌های طراحی شبکه‌ای، بازی‌های تراکمی هستند. در نتیجه آنها یک تابع پتانسیل دارند: $\textstyle \Phi =\sum _{e}\sum _{i=1}^{n_{e}}{\frac {c_{e}}{i}}$

قضیه. [قضیه ۱۹٫۱۳ از مرجع ۱] فرض کنید ثابت‌های $A$ و $B$ای برای هر استراتژی $S$ وجود دارد و $A\cdot SC(S)\leq \Phi (S)\leq B\cdot SC(S)$. در این صورت هزینه پایداری کوچک‌تر از $B/A$ خواهد بود.

اثبات. مقدار کمینهٔ $NE$ ِ $\Phi$ یک تعادل نش است؛ بنابراین: $SC(NE)\leq 1/A\cdot \Phi (NE)\leq 1/A\cdot \Phi (OPT)\leq B/A\cdot SC(OPT)$.

حال چون هزینهٔ اجتماعی مجموع هزینه‌های یال‌هاست، در نتیجه: $\Phi (S)=\sum _{e\in S}\sum _{i=1}^{n_{e}}{\frac {c_{e}}{i}}=\sum _{e\in S}c_{e}H_{n_{e}}\leq \sum _{e\in S}c_{e}H_{n}=H_{n}\cdot SC(S)$.

ما معمولاً $A=1$ در نظر می‌گیریم و محاسبات بالا $B=H_{n}$ به‌دست می‌دهد؛ پس ما توانستیم قضیه را ثابت کنیم.

جستارهای وابسته

• نظریه بازی‌ها
• اقتصاد ریاضی

منابع

1. L. Agussurja and H. C. Lau. The Price of Stability in Selfish Scheduling Games. Web Intelligence and Agent Systems: An International Journal, 9:4, 2009.