مسئله ۱۰۰ زندانی

۱۰۰ عدد زندانی موجودند که شماره‌های ۱ تا ۱۰۰ دارند و ۱۰۰ تا کشو وجود دارد که درون هر کدام یکی از اعداد ۱ تا ۱۰۰ وجود دارد هر زندانی می‌تواند بدون اینکه با دیگر زندانی‌ها صحبت کند ۵۰ تا از این کشوها را باز کند. در صورتی جان سالم به در می‌برند که همه زندانی‌ها شماره‌های خود را پیدا کرده باشند (اگر حتی یک نفر شماره خود را پیدا نکند همه زندانی خواهند ماند). دانشمندی دانمارکی به نام پیتر برو میلترسون برای اولین بار در سال ۲۰۰۳ استراتژی ای برای این مسئله ارائه کردند که شانس خوبی برای نجات یافتن همهٔ زندانی‌ها باشد.

رندوم برداشتن کشوها

اگر یک زندانی ۵۰ کشو را با هم به صورت رندوم انتخاب کند به احتمال ۵۰٪ عددش در ۵۰ کشویی است که انتخاب کرده در نتیجه احتمال اینکه همه نجات یابند برابر است با:

(½)¹⁰⁰ ≈ 0.0000000000000000000000000000008

استراتژی اصلی

در این استراتژی ما ۵۰ کشو را با هم انتخاب نمی‌کنیم و از اطلاعات ای که با باز کردن کشو به دست می‌آوریم استفاده می‌کنیم. اول کشوها را به ترتیب ۱ تا ۱۰۰ شماره‌گذاری می‌کنیم.
سپس زندانی شمارهٔ i ام کشوی شمارهٔ i ام را اول باز می‌کند اگر عدد درون آن i بود پس او نجات یافته‌است. اگر نه کشوای که شمارهٔ ان برابر با شمارهٔ درون کشو است را باز می‌کنیم.
این عملیات را تا زمانی که ۵۰ کشو را انتخاب کرده باشید ادامه می‌دهد اگر در حین عملیات به i برسد زندانی نجات می‌یابد.

مثال

فرض کنید اعداد درون کشوها این‌گونه باشند:

شمارهٔ کشو	۱	۲	۳	۴	۵	۶	۷	۸
شمارهٔ زندانی	۷	۴	۶	۸	۱	۳	۵	۲

در استراتژی ما هر زندانی این کارها را انجام می‌دهد:

زندانی ۱ کشو ی شمارهٔ ۱ را باز می‌کند بعد در ان ۷ را می‌بیند. بعد کشو ی شمارهٔ ۷ را باز می‌کند بعد در ان ۵ را می‌بیند. بعد کشو ی شمارهٔ ۵ را باز می‌کند بعد در ان شمارهٔ خود را می‌بیند و نجات می‌یابد.
زندانی ۲ کشو ی شمارهٔ ۲ و ۴و ۸ را باز می‌کند بعد در ۸ شمارهٔ خود را می‌بیند و نجات می‌یابد.
زندانی ۳ کشو ی شمارهٔ ۳ و ۶ را باز می‌کند بعد در ۶ شمارهٔ خود را می‌بیند و نجات می‌یابد.
زندانی ۴ کشو ی شمارهٔ ۴ و ۸و ۲ را باز می‌کند بعد در ۲ شمارهٔ خود را می‌بیند و نجات می‌یابد.
همینگونه زندانی‌های ۵ تا هم شمارهٔ خود را پیدا می‌کنند.

در مثال بالا همه شمارهٔ خود را پیدا کردند اما همیشه اینطور نیست مثلاً فرض کنید اعداد درون کشوها این‌گونه باشد:

شمارهٔ کشو	۱	۲	۳	۴	۵	۶	۷	۸
شمارهٔ زندانی	۳	۱	۷	۵	۸	۶	۴	۲

در این مثال زندانی اول کشوهای ۱ و ۳ و ۷ و۴ را باز می‌کند اما شمارهٔ خود را در آن پیدا نمی‌کند اما زندانی ۶ شمارهٔ خود را در اولین کشویی که باز می‌کند پیدا می‌کند.

احتمال نجات یافتن همه

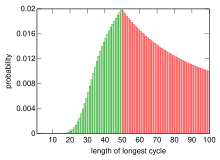
اعداد درون این کشوها در واقع جایگشتی از اعداد ۱ تا ۱۰۰ است. در نتیجه عدد اولی که زندانی i انتخاب می‌کند راس متصل به i در گراف جایگشت ان جایگشت است پس اگر دوری که راس i ام در ان است کوچکتر از ۵۰ باشد زندانی نجات می‌یابد.
در نتیجه اگر تمام دور‌های گراف طولشان کمتر از ۵۰ باشد همه نجات می‌یابند، یا به عبارت دیگر اگر طول ماکسیمم دور گراف کمتر مساوی ۵۰ باشد همه نجات می‌یابند.

اگر $l>50$ تعداد گراف‌هایی که طول بزرگ‌ترین دور ان ۵۰ است برابر است با:

${\binom {100}{l}}\cdot (l-1)!\cdot (100-l)!={\frac {100!}{l}}$ .

اثبات

اگر $l>50$ و l راس از رئوس گراف را انتخاب کنیم طول بزرگترین دور گراف برابر l خواهد بود چون تعداد بقیهٔ رأس‌ها از ۵۰ کمتر است حال l تا از رأس‌ها را انتخاب می‌کنیم $(l-1)!$ تا از گراف‌ها از l راسی که انتخاب کردیم تشکیل یک دور می‌دهند $(100-l)$ راس باقی‌مانده هم تشکیل یک گراف می‌دهند پس $(100-l)!$ حالت برای بقیهٔ رأس‌ها موجود است. احتمال اینکه ماکسیمم دور بزرگتر از ۵۰ باشد برابر است با

${\frac {1}{100!}}\left({\frac {100!}{51}}+\ldots +{\frac {100!}{100}}\right)$ در نتیجه احتمال اینکه ماکسیمم دور کمتر مساوی ۱۰۰ باشد برابر است با

$1-{\frac {1}{100!}}\left({\frac {100!}{51}}+\ldots +{\frac {100!}{100}}\right)=1-\left({\frac {1}{51}}+\ldots +{\frac {1}{100}}\right)=1-(H_{100}-H_{50})\approx 0.31183$ ،

که در ان $H_{n}$ عدد n ام سری هارمونیک است. پس دیدم به طرز شگفت‌آوری در ۳۱٪ مواقع همهٔ زندانی‌ها با این استراتژی نجات می‌یابند.

احتمال نجات یافتن همه در حالت کلی

حالا اگر به جای ۱۰۰ عدد دلخواه 2n را بگذاریم احتمال نجات یافتن همه با استراتژی اصلی برابر است با:

1-(H_{2n}-H_{n})=1-(H_{2n}-\ln 2n)+(H_{n}-\ln n)-\ln 2

.

با استفاده از ثابت اویلر-ماسکرونی $\gamma$ در $n\to \infty$ معادله به این صورت ساده می‌شود:

\lim _{n\to \infty }(H_{n}-\ln n)=\gamma

.

پس از آنجایی که معادله نزولی است به ازای هر n بیش از ۳۰٪ احتمال دارد که همه نجات یابند.

بهینگی

ما بهینگی روش گفته شده را برای سادگی برای $n=10$ . ثابت می‌کنیم و به ازای nهای دیگر اثبات مشابه دارد.
اول یک بازی جدید به نام بازی ۲ را این‌گونه تعریف می‌کنیم نفر اول می‌آید و آنقدر کشو باز می‌کند تا به شمارهٔ ۱ برسد بعد فردی که کوچک‌ترین شماره‌ای که نفر اول برنداشته را دارد می‌آید و همین کار را می‌کند و این روند ادامه پیدا می‌کند. حالا اگر یک نفر بیش از ۵ کشو باز کند بازی را باخته‌ایم.
حالا وقتی تمام ۱۰ کشو باز شد ۱۰ عدد انتخاب شده تشکیل یک جایگشت از اعداد ۱ تا ۱۰ می‌دهند مثلاً ۲٬۶٬۱٬۴٬۹٬۷٬۱۰٬۸٬۳٬۵ حالا احتمال اینکه نفر اول کشوی شامل ۲ را انتخاب کند برابر است با $1/10$ و همین‌طور احتمال اینکه بعد آن ۱۰ را انتخاب کند برابر است با $1/9$ در نتیجه احتمال اینکه هر جایگشت دلخواه انتخاب شود برابر $1/10!$ است. در نتیجه پیروزی در بازی دوم مستقل از استراتژی است
حال همهٔ اعدادی که یک نفر انتخاب کرده را در یک دسته قرار می‌دهیم برای مثال ارائه شده در بالا این‌گونه می‌شود: (۵)(۴٬۹٬۷٬۱۰٬۸٬۳)(۲٬۶٬۱) حال اثبات می‌کنیم هر دسته‌بندی این شکلی را می‌توان با دورهای یک گراف جایگشت تناظر یک به یک داد. اثبات: دورهای یک گراف جایگشت را در نظر گیرید اعداد هر دور را طوری بچرخانید که عدد مینیمم آخر قرار گیرد و دورها را به ترتیب مینیمم‌هایشان مرتب کنید این معادل یک دسته‌بندی از بازی ۲ می‌شود
مثال: (۲٬۴٬۶)(۱٬۳٬۱۰٬۵)(۹٬۷٬۸) -> (۸٬۹٬۷)(۴٬۶٬۲)(۳٬۱۰٬۵٬۱) = ۷ ۹ ۸ ۲ ۶ ۴ ۱ ۵ ۱۰ ۳
پس نتیجه می‌گیریم که احتمال اینکه در بازی دوم پیروز شویم برابر با احتمال این است که گراف دور بزرگتر از ۵ نداشته باشئ که احتمال ان در بالا محاسبه شده‌است.
حال یک استراتژی در بازی اول (همان استراتژی اصلی) را در نظر بگیرید هر کاری که یک زندانی در این استراتژی انجام می‌دهد می‌تواند در بازی دوم انجام دهد و اگر نفری قبل از او یک کشو را باز کرده بود دیگر لازم نیست باز کند در هر استراتژی ای که با آن بازی اول را بتوان برد بازی دوم هم می‌توان برد.
در نتیجه احتمال اینکه به ازای هر استرتژی بتوان بازی اول را برد کمتر از احتمال بردن بازی دوم است (که مستقل از استراتژی است) در نتیجه استراتژی ای که ارائه کردیم بهترین استراتژی است.^[۱]