مدل موریس-لکار

مدل موریس-لکار یک مدل زیستی از نورون است که توسط کاترین موریس و هارولد لکار توسعه یافته است. این مدل برای شبیه‌سازی انواع رفتارهای نوسانی در ارتباط با هدایت کلسیم (Ca++) و پتاسیم (K+) در تارهای عضلانی صدف بزرگ طراحی شده است. نورون‌های موریس-لکار توانایی نمایش هر دو نوع تحریک‌پذیری نورون کلاس I و کلاس II را دارند.

تاریخچه

کاترین موریس (متولد ۲۴ دسامبر ۱۹۴۹) یک زیست‌شناس کانادایی است. او با دریافت بورس تحصیلی مشترک‌المنافع به دانشگاه کمبریج رفت و در سال ۱۹۷۷ دکترای خود را دریافت کرد. موریس در اوایل دهه ۱۹۸۰ به عنوان استاد در دانشگاه اتاوا مشغول به کار شد. از سال ۲۰۱۵، او استاد بازنشسته این دانشگاه است.

هارولد لکار (۱۸ اکتبر ۱۹۳۵ – ۴ فوریه ۲۰۱۴) استاد زیست‌فیزیک و عصب‌شناسی در دانشگاه کالیفرنیا، برکلی بود. او در سال ۱۹۶۳ دکترای خود در رشته فیزیک را از دانشگاه کلمبیا دریافت کرد.

روش تجربی

آزمایش‌های موریس-لکار بر روش گیره ولتاژ ایجاد شده توسط کینز و همکاران تکیه داشتند. (1973).[1]

از نمونه‌های بزرگ صدف دریایی Balanus nubilus (از Pacific Bio-Marine Laboratories Inc., ونیز، کالیفرنیا) استفاده شد. صدف به دو نیمه جانبی برش داده شد و عضلات depressor scutorum rostralis به دقت نمایان شدند. فیبرهای جداگانه از محل تاندون برش داده شدند. انتهای دیگر عضله نزدیک به نقطه اتصال آن به صدف بریده شده و گره زده شد. فیبرهای جدا شده یا بلافاصله مورد استفاده قرار گرفتند یا تا حداکثر ۳۰ دقیقه در آب دریا مصنوعی استاندارد (ASW؛ توضیحات در ادامه) نگهداری شدند. آزمایش‌ها در دمای اتاق ۲۲ درجه سانتی‌گراد انجام شدند.

مفروضات اصلی زیربنای مدل موریس-لکار

معادلات برای یک تکه ایزو پتانسیل فضایی غشاء اعمال می شود. دو جریان ثابت (غیرغیرفعال) دردار ولتاژ با پتانسیل معکوس بایاس مخالف وجود دارد. جریان دپولاریزه توسط یون های Na+ یا Ca2+ (یا هر دو)، بسته به سیستمی که باید مدل سازی شود، حمل می شود، و جریان هایپرپولاریزه توسط K+ حمل می شود.
گیت‌های فعال‌سازی تغییرات پتانسیل غشا را به‌قدری سریع دنبال می‌کنند که رسانایی فعال‌کننده می‌تواند فوراً در هر ولتاژی به مقدار حالت پایدار خود رها شود.
دینامیک متغیر بازیابی را می توان با یک معادله دیفرانسیل خطی مرتبه اول برای احتمال باز شدن کانال تقریب زد. ^[۱]

توضیحات فیزیولوژیکی

مدل موریس-لکار یک سیستم دو‌بُعدی از معادلات دیفرانسیل غیرخطی است. این مدل در مقایسه با مدل چهار‌بُعدی هاجکین-هاکسلی به عنوان مدلی ساده‌تر در نظر گرفته می‌شود.

این سیستم معادلات به صورت کیفی رابطه پیچیده بین پتانسیل غشاء و فعال‌سازی کانال‌های یونی درون غشاء را توصیف می‌کند: پتانسیل به فعالیت کانال‌های یونی وابسته است و فعالیت کانال‌های یونی نیز به ولتاژ بستگی دارد. با تغییر پارامترهای چند شاخگی، انواع مختلفی از رفتارهای نورونی نمایش داده می‌شوند. τN با مقیاس‌های زمانی نسبی دینامیک شلیک مرتبط است که به طور گسترده‌ای از یک سلول به سلول دیگر متغیر است و وابستگی قابل توجهی به دما نشان می‌دهد.

از نظر کمی:

{\begin{aligned}C{\frac {dV}{dt}}&~=~I-g_{\mathrm {L} }(V-V_{\mathrm {L} })-g_{\mathrm {Ca} }M_{\mathrm {ss} }(V-V_{\mathrm {Ca} })-g_{\mathrm {K} }N(V-V_{\mathrm {K} })\\[5pt]{\frac {dN}{dt}}&~=~{\frac {N_{\mathrm {ss} }-N}{\tau _{N}}}\end{aligned}}

{\begin{aligned}M_{\mathrm {ss} }&~=~{\frac {1}{2}}\cdot \left(1+\tanh \left[{\frac {V-V_{1}}{V_{2}}}\right]\right)\\[5pt]N_{\mathrm {ss} }&~=~{\frac {1}{2}}\cdot \left(1+\tanh \left[{\frac {V-V_{3}}{V_{4}}}\right]\right)\\[5pt]\tau _{N}&~=~1/\left(\varphi \cosh \left[{\frac {V-V_{3}}{2V_{4}}}\right]\right)\end{aligned}}

توجه داشته باشید که معادلات Mss و Nss می‌توانند به صورت زیر نیز بیان شوند:

Mss = (1 + exp[−2(V − V1) / V2])−1

Nss = (1 + exp[−2(V − V3) / V4])−1

با این حال، بیشتر نویسندگان ترجیح می‌دهند از شکل معادلات با استفاده از توابع هذلولوی استفاده کنند.

متغیرها

V: پتانسیل غشایی
N:متغیر بازیابی: احتمالی که کانال K+ در حال انجام است

پارامترها و ثابت ها

I: جریان اعمال شده
C: ظرفیت غشا
gL، gCa، gK : رسانایی نشت، Ca++ و K+ از طریق کانال غشاء
VL، VCa، VK : پتانسیل تعادل کانال‌های یونی مربوطه
V1، V2، V3، V4: پارامترهای تنظیم برای حالت پایدار و ثابت زمانی
φ: فرکانس مرجع

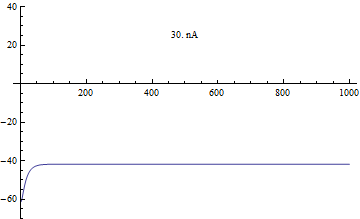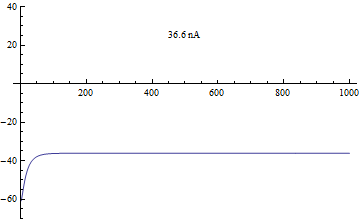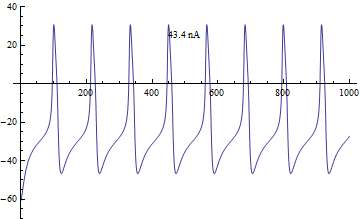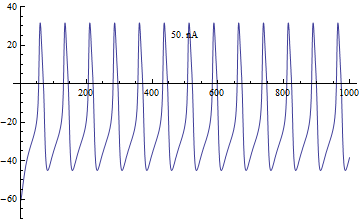
چندشاخگی ها

↑ این فرض هرگز دقیقاً درست نیست، زیرا پروتئین های کانال از زیر واحدهایی تشکیل شده اند که برای رسیدن به حالت باز باید هماهنگ عمل کنند. علیرغم عدم تأخیر در شروع بازیابی، به نظر می رسد این مدل برای ملاحظات صفحه فاز برای بسیاری از سیستم های تحریک پذیر کافی است.

Possible Bifurcations

Hopf Bifurcation

SNIC bifurcation

Homoclinic bifurcation

Current clamp simulations of the Morris–Lecar model. The injected current for the SNIC bifurcation and the homoclinic bifurcation is varied between 30 nA and 50 nA, while the current for the Hopf bifurcation is varied between 80nA and 100nA

همچنین ببینید

مراجع

[scholar-1] این فرض هرگز دقیقاً درست نیست، زیرا پروتئین های کانال از زیر واحدهایی تشکیل شده اند که برای رسیدن به حالت باز باید هماهنگ عمل کنند. علیرغم عدم تأخیر در شروع بازیابی، به نظر می رسد این مدل برای ملاحظات صفحه فاز برای بسیاری از سیستم های تحریک پذیر کافی است.

[۱]