دستگاه مختصات کروی

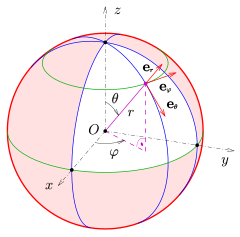
نقطه‌ای که با دستگاه مختصات کروی نمایش داده شده‌است

در ریاضیات، دستگاه مختصات کروی یک دستگاه مختصات برای نمایش حساب‌ها و اعداد هندسی در فضای سه بعدی با استفاده از سه مختصه است:

• فاصلهٔ شعاعی یک نقطه از یک مبدأ ثابت (اصطلاحا رو $\rho$)
• زاویهٔ سمت‌الرأس (zenith angle) از قسمت مثبت محور z (اصطلاحاً فی $\varphi$ یا $\phi$)
• زاویهٔ گرایی (azimuth angle) از قسمت مثبت محور x (اصطلاحاً تتا $\theta$)

تعریف

در ریاضیات مختصات کروی،برای فضای سه بعدی است که در آن موقعیت یک نقطه با سه عدد مشخص می شود: فاصله شعاعی آن نقطه از یک مبدأ ثابت، زاویه قطبی آن اندازه گیری شده از یک جهت اوج ثابت ، و زاویه متعامد برآمدگی متعامد آن بر روی صفحه مرجعی که از مبدا می گذرد و متعامد به نقطه اوج است، از یک جهت مرجع ثابت در آن صفحه اندازه گیری می شود. می توان آن را نسخه سه بعدی سیستم مختصات قطبی دید .

استفاده از نمادها و ترتیب مختصات در منابع و رشته ها متفاوت است. این مقاله از کنوانسیون ISO  که اغلب در فیزیک با آن مواجه می‌شود، استفاده می‌کند :فاصله شعاعی، زاویه قطبی و زاویه ازیموت را نشان می دهد. در بسیاری از کتاب های ریاضی،یافاصله شعاعی، زاویه ازیموتال و زاویه قطبی را نشان می‌دهد و معانی θ و φ را تغییر می‌دهد . قراردادهای دیگری نیز استفاده می شود، مانند r برای شعاع از محور z ، بنابراین باید دقت زیادی برای بررسی معنای نمادها انجام شود.

طبق قراردادهای سیستم های مختصات جغرافیایی ، موقعیت ها با طول و عرض جغرافیایی و ارتفاع (ارتفاع) اندازه گیری می شوند. تعدادی سیستم مختصات آسمانی بر اساس صفحات بنیادی مختلف و با اصطلاحات مختلف برای مختصات مختلف وجود دارد. سیستم های مختصات کروی مورد استفاده در ریاضیات معمولاً به جای درجه از رادیان استفاده می کنند و زاویه آزیموتال را در خلاف جهت عقربه های ساعت از محور x به محور y اندازه می گیرند نه در جهت عقربه های ساعت از شمال (0 درجه) به شرق (90 درجه) مانند سیستم مختصات افقی . .  زاویه قطبی اغلب با زاویه جایگزین می شودزاویه ارتفاع از صفحه مرجع اندازه گیری می شود، به طوری که زاویه ارتفاع صفر در افق باشد.

سیستم مختصات کروی سیستم مختصات قطبی دو بعدی را تعمیم می دهد. همچنین می توان آن را به فضاهای با ابعاد بالاتر گسترش داد و سپس به عنوان یک سیستم مختصات ابرکره ای نامیده می شود .

مشخصات

دستگاه مختصات کروی، دستگاه مختصاتی با سه مختصه‌است:

• مختصه $\rho$ (یا $r$) که روی کره‌های هم مرکز حول مبدأ است.
• مختصه $\theta$ روی مخروط‌های دوار قائم حول محور $z$ با راس واقع در مبدأ.
• مختصه $\phi$ که روی نیم صفحاتی که از محور قطبی $z$ می‌گذرد.

در فیزیک بنا به سنت جای $\theta$ و $\phi$ معکوس است یعنی $\theta$ زاویه با محور $z$ است.

تعمیم

در مختصات کروی،همچنین می توان با استفاده از نسخه اصلاح شده مختصات کروی با بیضی ها در مختصات دکارتی مقابله کرد.فرض کنید P یک بیضی مشخص شده توسط مجموعه سطح باشد

$ax^{2}+by^{2}+cz^{2}=d.$

مختصات کروی اصلاح شده یک نقطه در P در کنوانسیون ISO (یعنی برای فیزیک: شعاع r، تمایل θ، آزیموت φ) را می توان از مختصات دکارتی آن (x, y, z) با فرمول بدست آورد.

${\begin{aligned}x&={\frac {1}{\sqrt {a}}}r\sin \theta \,\cos \varphi ,\\y&={\frac {1}{\sqrt {b}}}r\sin \theta \,\sin \varphi ,\\z&={\frac {1}{\sqrt {c}}}r\cos \theta ,\\r^{2}&=ax^{2}+by^{2}+cz^{2}.\end{aligned}}$

یک عنصر حجم بی نهایت کوچک توسط

$\mathrm {d} V=\left|{\frac {\partial (x,y,z)}{\partial (r,\theta ,\varphi )}}\right|\,dr\,d\theta \,d\varphi ={\frac {1}{\sqrt {abc}}}r^{2}\sin \theta \,\mathrm {d} r\,\mathrm {d} \theta \,\mathrm {d} \varphi ={\frac {1}{\sqrt {abc}}}r^{2}\,\mathrm {d} r\,\mathrm {d} \Omega .$

ضریب ریشه مربع از خاصیت دترمینان می آید که اجازه می دهد یک ثابت از یک ستون خارج شود:

${\begin{vmatrix}ka&b&c\\kd&e&f\\kg&h&i\end{vmatrix}}=k{\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}.$

محدوده مختصات

سه مختصه در محدوده‌های زیر می‌توانند باشند:

• مختصه $\rho$ (یا $r$):

$0\leq \rho$

• مختصه زاویه قطبی $\theta$:

$0\leq \theta \leq 2\pi$

• مختصه زاویه سمتی $\phi$:

$0\leq \phi \leq \pi$

رابطه با مختصات دکارتی

مختصات دستگاه کروی را با استفاده از روابط زیر به دستگاه مختصات دکارتی می‌توان تبدیل کرد:

• برای مختصه $\rho$:

${\rho }={\sqrt {x^{2}+y^{2}+z^{2}}}$

• برای مختصه زاویه قطبی $\theta$:

${\theta }=\arctan \left({\frac {y}{x}}\right)$

• برای مختصه زاویه سمتی $\phi$:

${\phi }=\arccos \left({\frac {z}{\sqrt {x^{2}+y^{2}+z^{2}}}}\right)$

مختصات دکارتی نیز را با روابط زیر می‌توان به دستگاه مختصات کروی برد:

• مختصه $x$:

${x}=\rho \,\sin \phi \,\cos \theta \quad$

• مختصه $y$:

${y}=\rho \,\sin \phi \,\sin \theta \quad$

• مختصه $z$:

${z}=\rho \,\cos \phi \quad$

فاصله بین دونقطه

در مختصات کروی، با توجه به دو نقطه که φ مختصات ازیموتال است:

${\begin{aligned}{\mathbf {r} }&=(r,\theta ,\varphi ),\\{\mathbf {r} '}&=(r',\theta ',\varphi ')\end{aligned}}$

فاصله بین دو نقطه را می توان به روش زیر بیان کرد:${\begin{aligned}{\mathbf {D} }&={\sqrt {r^{2}+r'^{2}-2rr'(\sin {\theta }\sin {\theta '}\cos {(\varphi -\varphi ')}+\cos {\theta }\cos {\theta '})}}\end{aligned}}$

تبدیل سیستم مختصات های دیگر به مختصات کروی

از آنجایی که،سیستم مختصات کروی تنها یکی از سیستم های مختصات سه بعدی است، معادلاتی برای تبدیل مختصات های دیگر بین سیستم مختصات کروی و سایرین وجود دارد.

مختصات کارتزین

درمختصات کروی یک نقطه را در کنوانسیون ISO (یعنی برای فیزیک: شعاع:r، شیب:θ، آزیموت:φ)را می توان از مختصات دکارتی آن(x، y، z)بافرمول بدست آورد.

${\begin{aligned}r&={\sqrt {x^{2}+y^{2}+z^{2}}}\\\theta &=\arccos {\frac {z}{\sqrt {x^{2}+y^{2}+z^{2}}}}=\arccos {\frac {z}{r}}=\arctan {\frac {\sqrt {x^{2}+y^{2}}}{z}}\\\varphi &={\begin{cases}\arctan({\frac {y}{x}})&{\text{if }}x>0,\\\arctan({\frac {y}{x}})+\pi &{\text{if }}x<0{\text{ and }}y\geq 0,\\\arctan({\frac {y}{x}})-\pi &{\text{if }}x<0{\text{ and }}y<0,\\+{\frac {\pi }{2}}&{\text{if }}x=0{\text{ and }}y>0,\\-{\frac {\pi }{2}}&{\text{if }}x=0{\text{ and }}y<0,\\{\text{undefined}}&{\text{if }}x=0{\text{ and }}y=0.\end{cases}}\end{aligned}}$در اینجا مماس معکوسφبا آرکتانژانتy/xنشان داده است که باید با در نظر گرفتن ربع صحیح (x,y) به طور مناسب تعریف شود.

از طرف دیگر،این تبدیل را می توان به عنوان دو تبدیل متوالی مستطیلی به قطبی درنظر گرفت: اولین مورد در صفحه x,y دکارتی از(x,y) به(R,φ)است،که درآنR طرح ریزیr بر روی صفحه x,y است و دوم در صفحه z,R دکارتی از (z,R) تا (r,θ). ربع صحیح برای φوθ با صحت تبدیل مستطیل مسطح به قطبی مشخص می شود. این فرمول ها فرض می کنند که دو سیستم منشأ یکسانی دارند، صفحه مرجع کروی صفحه xy دکارتی است، θ از جهت z تمایل دارد، و زوایای آزیموت از محور x دکارتی اندازه گیری می شود (به طوری که محور y دارای φ = +90 درجه). اگر θ ارتفاع را از صفحه مرجع به جای شیب از نقطه اوج اندازه گیری کند، آرکوس بالا به یک کمان تبدیل می شود، و cos θ و sin θ پایین سوئیچ می شوند. برعکس، مختصات دکارتی ممکن است از مختصات کروی (شعاع r، تمایل θ، آزیموت φ)، جایی که:

[r∈ [0، ∞)، θ∈ [0، π]، φ∈ [0، 2π]

واحد های مختصاتی(y,x,z)طبق مختصات کروی به صورت زیر محاسبه می گردد:

${\begin{aligned}x&=r\cos \varphi \,\sin \theta ,\\y&=r\sin \varphi \,\sin \theta ,\\z&=r\cos \theta .\end{aligned}}$

مختصات استوانه ای

مختصات استوانه ای (شعاع محوری ρ، آزیموت φ، ارتفاع z) ممکن است با فرمول ها به مختصات کروی (شعاع مرکزی r، تمایل θ، آزیموت φ) تبدیل شوند.

${\begin{aligned}r&={\sqrt {\rho ^{2}+z^{2}}},\\\theta &=\arctan {\frac {\rho }{z}}=\arccos {\frac {z}{\sqrt {\rho ^{2}+z^{2}}}},\\\varphi &=\varphi .\end{aligned}}$

مختصات استوانه ای به هیچ دستگاهی تبدیل نمی شود حتی مختصات کروی،ولی برعکس؛مختصات کروی ممکن است بر اساس فرمول ها یه مختصات ها الخصوص مختصات استوانه اس تبدیل شود.

حساب برداری

• بردار $A$ در مختصات کروی به صورت زیر نمایش داده می‌شود:

${\overrightarrow {A}}=A_{r}{\boldsymbol {\hat {r}}}+A_{\theta }{\boldsymbol {\hat {\theta }}}+A_{\phi }{\boldsymbol {\hat {\phi }}}$

• ضرب داخلی و ضرب خارجی بردارها مانند تمامی دستگاه‌های مختصّات متعامد به همان فرمولبندی دستگاه مختصات دکارتی انجام می‌شود.
• گرادیان تابع اسکالر $f$ به صورت زیر است:

$\nabla f={\partial f \over \partial r}{\boldsymbol {\hat {r}}}+{1 \over r}{\partial f \over \partial \theta }{\boldsymbol {\hat {\theta }}}+{1 \over r\sin \theta }{\partial f \over \partial \phi }{\boldsymbol {\hat {\phi }}}$

• واگرایی بردار $A$:

$\nabla \cdot \mathbf {A} ={1 \over r^{2}}{\partial \left(r^{2}A_{r}\right) \over \partial r}+{1 \over r\sin \theta }{\partial \over \partial \theta }\left(A_{\theta }\sin \theta \right)+{1 \over r\sin \theta }{\partial A_{\phi } \over \partial \phi }$

• کرل بردار $A$ در دستگاه کروی:

$\nabla \times \mathbf {A} ={1 \over r\sin \theta }\left({\partial \over \partial \theta }(A_{\phi }\sin \theta )-{\partial A_{\theta } \over \partial \phi }\right){\boldsymbol {\hat {r}}}+{1 \over r}\left({1 \over \sin \theta }{\partial A_{r} \over \partial \phi }-{\partial \over \partial r}\left(rA_{\phi }\right)\right){\boldsymbol {\hat {\theta }}}+{1 \over r}\left({\partial \over \partial r}\left(rA_{\theta }\right)-{\partial A_{r} \over \partial \theta }\right){\boldsymbol {\hat {\phi }}}$

• عملگر لاپلاس بر روی $f$ در مختصات کروی:

$\Delta f=\nabla ^{2}f={1 \over r^{2}}{\partial \over \partial r}\left(r^{2}{\partial f \over \partial r}\right)+{1 \over r^{2}\sin \theta }{\partial \over \partial \theta }\left(\sin \theta {\partial f \over \partial \theta }\right)+{1 \over r^{2}\sin ^{2}\theta }{\partial ^{2}f \over \partial \phi ^{2}}$

تبدیل‌های دستگاه مختصات

دستگاه مختصات جغرافیایی

دستگاه مختصات جغرافیایی بک مدل دیگر از دستگاه مختصات کروی است که کاربرد اصلی آن در جغرافیا است اما در ریاضیات و فیزیک نیز استفاده‌هایی دارد. در جغرافی، ρ معمولاً حذف یا با مقداری که ارتفاع یا بلندی از سطح دریا را نشان می‌دهد جایگزین می‌شود.

عرض جغرافیایی ${\delta }\,$، مکمل سمت‌الرأس یا متمم عرض جغرافیایی است و می‌تواند با این روابط تبدیل شود:

${\delta }=90^{\circ }-\phi$

یا

${\phi }=90^{\circ }-\delta$

با این وجود عرض جغرافیایی عمدتاً با φ نیز نمایش داده می‌شود. این، یک زاویه سمت‌الرأس را که از صفحهٔ xy سرچشمه می‌گیرد با دامنهٔ ‎ -۹۰° ≤ φ ≤ ۹۰° ‏ بیان می‌کند. طول جغرافیایی به وسیلهٔ درجه به شرق یا به غرب از °۰ اندازه‌گیری می‌شود، بنابراین دامنه‌اش ‎ -۱۸۰° ≤ θ ≤ ۱۸۰° ‏ است.

دیفرانسیل‌ها

بردار واحد در مختصات کروی

المان خط برای جابه جایی بینهایت کوچک از (r, θ, φ) به (r + dr, θ + dθ, φ + dφ)برابر است با:

• دیفرانسیل خطی:

$d\mathbf {l} =dr\mathbf {\hat {r}} +rd\theta {\boldsymbol {\hat {\theta }}}+r\sin \theta d\phi {\boldsymbol {\hat {\phi }}}$

• دیفرانسیل سطحی:

$d\mathbf {S} =r^{2}\sin \phi d\theta d\phi \mathbf {\hat {r}} +r\sin \phi drd\phi {\boldsymbol {\hat {\theta }}}+rdrd\theta {\boldsymbol {\hat {\phi }}}$

• دیفرانسیل حجمی:

$dv=r^{2}\sin \phi drd\theta d\phi \,$

به ترتیب بردارهای واحد متعامد محلی در جهت افزایش r، θ و φ و هستند. x̂، ŷ و ẑ بردارهای واحد در مختصات دکارتی هستند. تبدیل خطی به این سه گانه مختصات راست دست یک ماتریس چرخش است،$$R={\begin{pmatrix}\sin \theta \cos \varphi &\sin \theta \sin \varphi &\cos \theta \\\cos \theta \cos \varphi &\cos \theta \sin \varphi &-\sin \theta \\-\sin \varphi &\cos \varphi &0\end{pmatrix}}.$$این تبدیل از کروی به دکارتی را می دهد، برعکس آن با معکوس آن مشخص می شود. نکته: ماتریس یک ماتریس متعامد است، یعنی معکوس آن به سادگی جابجایی آن است. بنابراین، بردارهای واحد دکارتی با بردارهای واحد کروی مرتبط هستند:$${\begin{bmatrix}\mathbf {\hat {x}} \\\mathbf {\hat {y}} \\\mathbf {\hat {z}} \end{bmatrix}}={\begin{bmatrix}\sin \theta \cos \varphi &\cos \theta \cos \varphi &-\sin \varphi \\\sin \theta \sin \varphi &\cos \theta \sin \varphi &\cos \varphi \\\cos \theta &-\sin \theta &0\end{bmatrix}}{\begin{bmatrix}{\boldsymbol {\hat {r}}}\\{\boldsymbol {\hat {\theta }}}\\{\boldsymbol {\hat {\varphi }}}\end{bmatrix}}$$شکل کلی فرمول برای اثبات عنصر خط دیفرانسیل، است:$$\mathrm {d} \mathbf {r} =\sum _{i}{\frac {\partial \mathbf {r} }{\partial x_{i}}}\,\mathrm {d} x_{i}=\sum _{i}\left|{\frac {\partial \mathbf {r} }{\partial x_{i}}}\right|{\frac {\frac {\partial \mathbf {r} }{\partial x_{i}}}{\left|{\frac {\partial \mathbf {r} }{\partial x_{i}}}\right|}}\,\mathrm {d} x_{i}=\sum _{i}\left|{\frac {\partial \mathbf {r} }{\partial x_{i}}}\right|\,\mathrm {d} x_{i}\,{\hat {\boldsymbol {x}}}_{i},$$یعنی تغییر در $\mathbf {r}$ به تغییرات فردی مربوط به تغییرات در مختصات فردی تجزیه می شود.

برای اعمال این مورد در مورد حاضر، باید محاسبه کرد که $\mathbf {r}$ چگونه با هر یک از مختصات در کنوانسیون های مورد استفاده تغییر می کند؟

جواب به این صورت است:$$\mathbf {r} ={\begin{bmatrix}r\sin \theta \,\cos \varphi \\r\sin \theta \,\sin \varphi \\r\cos \theta \end{bmatrix}}.$$بدین ترتیب:$${\frac {\partial \mathbf {r} }{\partial r}}={\begin{bmatrix}\sin \theta \,\cos \varphi \\\sin \theta \,\sin \varphi \\\cos \theta \end{bmatrix}},\quad {\frac {\partial \mathbf {r} }{\partial \theta }}={\begin{bmatrix}r\cos \theta \,\cos \varphi \\r\cos \theta \,\sin \varphi \\-r\sin \theta \end{bmatrix}},\quad {\frac {\partial \mathbf {r} }{\partial \varphi }}={\begin{bmatrix}-r\sin \theta \,\sin \varphi \\r\sin \theta \,\cos \varphi \\0\end{bmatrix}}.$$ضرایب مورد نظر، بزرگی این بردارها هستند:$$\left|{\frac {\partial \mathbf {r} }{\partial r}}\right|=1,\quad \left|{\frac {\partial \mathbf {r} }{\partial \theta }}\right|=r,\quad \left|{\frac {\partial \mathbf {r} }{\partial \varphi }}\right|=r\sin \theta .$$عنصر سطحی که از θ تا θ + dθ و φ تا φ + dφ را در یک سطح کروی در شعاع r (ثابت) پوشانده است، سپس:$$\mathrm {d} S_{r}=\left\|{\frac {\partial {\mathbf {r} }}{\partial \theta }}\times {\frac {\partial {\mathbf {r} }}{\partial \varphi }}\right\|\mathrm {d} \theta \,\mathrm {d} \varphi =\left|r{\hat {\boldsymbol {\theta }}}\times r\sin \theta {\boldsymbol {\hat {\varphi }}}\right|=r^{2}\sin \theta \,\mathrm {d} \theta \,\mathrm {d} \varphi ~.$$بنابراین زاویه جامد دیفرانسیل برابر است با:$$\mathrm {d} \Omega ={\frac {\mathrm {d} S_{r}}{r^{2}}}=\sin \theta \,\mathrm {d} \theta \,\mathrm {d} \varphi .$$عنصر سطح در سطحی با زاویه قطبی θ ثابت (یک مخروط با راس مبدأ) است$$\mathrm {d} S_{\theta }=r\sin \theta \,\mathrm {d} \varphi \,\mathrm {d} r.$$عنصر سطح در سطحی با آزیموت φ ثابت (نیم صفحه عمودی) است:$$\mathrm {d} S_{\varphi }=r\,\mathrm {d} r\,\mathrm {d} \theta .$$عنصر حجمی که از r تا r + dr، θ تا θ + dθ، و φ تا φ + dφ را شامل می‌شود، توسط تعیین‌کننده ماتریس ژاکوبین مشتقات جزئی مشخص می‌شود:$$J={\frac {\partial (x,y,z)}{\partial (r,\theta ,\varphi )}}={\begin{pmatrix}\sin \theta \cos \varphi &r\cos \theta \cos \varphi &-r\sin \theta \sin \varphi \\\sin \theta \sin \varphi &r\cos \theta \sin \varphi &r\sin \theta \cos \varphi \\\cos \theta &-r\sin \theta &0\end{pmatrix}},$$برای مثال:$$\mathrm {d} V=\left|{\frac {\partial (x,y,z)}{\partial (r,\theta ,\varphi )}}\right|\,\mathrm {d} r\,\mathrm {d} \theta \,\mathrm {d} \varphi =r^{2}\sin \theta \,\mathrm {d} r\,\mathrm {d} \theta \,\mathrm {d} \varphi =r^{2}\,\mathrm {d} r\,\mathrm {d} \Omega ~.$$بنابراین، برای مثال، یک تابع f(r، θ، φ) را می توان در هر نقطه در R³ توسط انتگرال سه گانه ادغام کرد.$$\int \limits _{0}^{2\pi }\int \limits _{0}^{\pi }\int \limits _{0}^{\infty }f(r,\theta ,\varphi )r^{2}\sin \theta \,\mathrm {d} r\,\mathrm {d} \theta \,\mathrm {d} \varphi ~.$$عملگر del در این سیستم به عبارات زیر برای گرادیان، واگرایی، کرل و (اسکالر) لاپلاسین منجر می شود.$${\begin{aligned}\nabla f={}&{\partial f \over \partial r}{\hat {\mathbf {r} }}+{1 \over r}{\partial f \over \partial \theta }{\hat {\boldsymbol {\theta }}}+{1 \over r\sin \theta }{\partial f \over \partial \varphi }{\hat {\boldsymbol {\varphi }}},\\[8pt]\nabla \cdot \mathbf {A} ={}&{\frac {1}{r^{2}}}{\partial \over \partial r}\left(r^{2}A_{r}\right)+{\frac {1}{r\sin \theta }}{\partial \over \partial \theta }\left(\sin \theta A_{\theta }\right)+{\frac {1}{r\sin \theta }}{\partial A_{\varphi } \over \partial \varphi },\\[8pt]\nabla \times \mathbf {A} ={}&{\frac {1}{r\sin \theta }}\left({\partial \over \partial \theta }\left(A_{\varphi }\sin \theta \right)-{\partial A_{\theta } \over \partial \varphi }\right){\hat {\mathbf {r} }}\\[8pt]&{}+{\frac {1}{r}}\left({1 \over \sin \theta }{\partial A_{r} \over \partial \varphi }-{\partial \over \partial r}\left(rA_{\varphi }\right)\right){\hat {\boldsymbol {\theta }}}\\[8pt]&{}+{\frac {1}{r}}\left({\partial \over \partial r}\left(rA_{\theta }\right)-{\partial A_{r} \over \partial \theta }\right){\hat {\boldsymbol {\varphi }}},\\[8pt]\nabla ^{2}f={}&{1 \over r^{2}}{\partial \over \partial r}\left(r^{2}{\partial f \over \partial r}\right)+{1 \over r^{2}\sin \theta }{\partial \over \partial \theta }\left(\sin \theta {\partial f \over \partial \theta }\right)+{1 \over r^{2}\sin ^{2}\theta }{\partial ^{2}f \over \partial \varphi ^{2}}\\[8pt]={}&\left({\frac {\partial ^{2}}{\partial r^{2}}}+{\frac {2}{r}}{\frac {\partial }{\partial r}}\right)f+{1 \over r^{2}\sin \theta }{\partial \over \partial \theta }\left(\sin \theta {\frac {\partial }{\partial \theta }}\right)f+{\frac {1}{r^{2}\sin ^{2}\theta }}{\frac {\partial ^{2}}{\partial \varphi ^{2}}}f~.\end{aligned}}$$علاوه بر این، ژاکوبین معکوس در مختصات دکارتی است$$J^{-1}={\begin{pmatrix}{\dfrac {x}{r}}&{\dfrac {y}{r}}&{\dfrac {z}{r}}\\\\{\dfrac {xz}{r^{2}{\sqrt {x^{2}+y^{2}}}}}&{\dfrac {yz}{r^{2}{\sqrt {x^{2}+y^{2}}}}}&{\dfrac {-(x^{2}+y^{2})}{r^{2}{\sqrt {x^{2}+y^{2}}}}}\\\\{\dfrac {-y}{x^{2}+y^{2}}}&{\dfrac {x}{x^{2}+y^{2}}}&0\end{pmatrix}}.$$تانسور متریک در سیستم مختصات کروی است:

$g=J^{T}J$.

تعمیم پ مختصات کروی به صورت n بعدی

تعمیم مختصات کروی به ابعاد $n$ اینگونه است:

${\begin{aligned}x_{1}&=r\cos(\phi _{1})\\x_{2}&=r\sin(\phi _{1})\cos(\phi _{2})\\x_{3}&=r\sin(\phi _{1})\sin(\phi _{2})\cos(\phi _{3})\\&{}\,\,\,\vdots \\x_{n-1}&=r\sin(\phi _{1})\cdots \sin(\phi _{n-2})\cos(\phi _{n-1})\\x_{n}&=r\sin(\phi _{1})\cdots \sin(\phi _{n-2})\sin(\phi _{n-1})\end{aligned}}$

زاویه ها بر اساس زیر توسعه می یابند:

${\begin{aligned}\tan(\phi _{n-1})&={\frac {x_{n}}{x_{n-1}}}\\\tan(\phi _{n-2})&={\frac {\sqrt {{x_{n}}^{2}+{x_{n-1}}^{2}}}{x_{n-2}}}\\&{}\,\,\,\vdots \\\tan(\phi _{1})&={\frac {\sqrt {{x_{n}}^{2}+{x_{n-1}}^{2}+\cdots +{x_{2}}^{2}}}{x_{1}}}\end{aligned}}$

شماره گذاری مجدد یک فرمول بازگشتی برای زوایا به دست می دهد:

${\begin{aligned}x_{n}&=r\cos(\phi _{n-1})\\x_{n-1}&=r\sin(\phi _{n-1})\cos(\phi _{n-2})\\x_{n-2}&=r\sin(\phi _{n-1})\sin(\phi _{n-2})\cos(\phi _{n-3})\\&{}\,\,\,\vdots \\x_{2}&=r\sin(\phi _{n-1})\cdots \sin(\phi _{2})\cos(\phi _{1})\\x_{1}&=r\sin(\phi _{n-1})\cdots \sin(\phi _{2})\sin(\phi _{1})\end{aligned}}$

که منجر به زوایای زیر می شود:

$\left\Vert {\vec {L}}_{k}\right\Vert =\operatorname {sgn}(x_{k}){\sqrt {x_{k}^{2}+\left\Vert {\vec {L}}_{k-1}\right\Vert ^{2}}}={\frac {x_{k}}{\left\Vert x_{k}\right\Vert }}{\sqrt {x_{k}^{2}+\left\Vert {\vec {L}}_{k-1}\right\Vert ^{2}}}$

mit $\left\Vert {\vec {L}}_{0}\right\Vert =0$ und

$\tan(\phi _{k})={\frac {\sqrt {x_{k}^{2}+\left\Vert {\vec {L}}_{k-1}\right\Vert ^{2}}}{x_{k+1}}}={\frac {\left\Vert {\vec {L}}_{k}\right\Vert }{x_{k+1}}}$

شعاع عبارت است از:

$r=\left\Vert {\vec {L}}_{n}\right\Vert$

تمایز موردی زاویه مناسب را به مختصات دکارتی با استفاده از Arcutangent برمی‌گرداند، جایی که $\arctan(\pm \,\infty )=\pm \,{\tfrac {\pi }{2}}$:

${\begin{aligned}\phi _{k}={\begin{cases}\arctan \left({\frac {\left\Vert {\vec {L}}_{k}\right\Vert }{x_{k+1}}}\right)+\pi ,&{\text{(1) wenn: }}x_{k+1}<0\;\land \;k=n-1\\\arctan \left({\frac {\left\Vert {\vec {L}}_{k}\right\Vert }{x_{k+1}}}\right),&{\text{(2) wenn: }}{\text{nicht (1)}}\land \;{\text{nicht (3)}}\\0,&{\text{(3) wenn: }}x_{k+1}=\left\Vert {\vec {L}}_{k}\right\Vert =0\\\end{cases}}\end{aligned}}$

Dabei fällt auf, dass ${\begin{aligned}{\vec {L}}_{k}\end{aligned}}$ immer ein zweidimensionaler Vektor ist für ${\begin{aligned}k>0\end{aligned}}$.

ماتریس ژاکوبین

ماتریس ژاکوبین مختصات کروی با توجه به شماره گذاری بالا می گوید:

$J=\left({\begin{matrix}\cos(\phi _{1})&-r\sin(\phi _{1})&0&0&\cdots &0\\\sin(\phi _{1})\cos(\phi _{2})&r\cos(\phi _{1})\cos(\phi _{2})&-r\sin(\phi _{1})\sin(\phi _{2})&0&\cdots &0\\\vdots &\vdots &\ddots &\ddots &\ddots &\vdots \\\vdots &\vdots &\ddots &\ddots &\ddots &0\\\sin(\phi _{1})\cdots \sin(\phi _{n-2})\cos(\phi _{n-1})&r\cos(\phi _{1})\cdots \sin(\phi _{n-2})\cos(\phi _{n-1})&\cdots &\cdots &\cdots &-r\sin(\phi _{1})\cdots \sin(\phi _{n-2})\sin(\phi _{n-1})\\\sin(\phi _{1})\cdots \sin(\phi _{n-2})\sin(\phi _{n-1})&r\cos(\phi _{1})\cdots \sin(\phi _{n-2})\sin(\phi _{n-1})&\cdots &\cdots &\cdots &r\sin(\phi _{1})\cdots \sin(\phi _{n-2})\cos(\phi _{n-1})\end{matrix}}\right)$

عامل تعیین کننده آن است:

$\det J_{(n)}=r^{n-1}\sin(\phi _{1})^{n-2}\sin(\phi _{2})^{n-3}\cdots \sin(\phi _{n-2})=\displaystyle r^{n-1}\cdot \prod _{k=2}^{n-1}\left(\sin(\phi _{n-k})\right)^{k-1}\quad n\geq 2$

انتگرال بیش از مقدار مطلق این تعیین کننده را می توان با تابع گاما $\Gamma$ به دست آورد:$\int _{0}^{R}\int _{0}^{2\pi }\int _{0}^{\pi }\dots \int _{0}^{\pi }|\det J_{(n)}|\,{\text{d}}\phi _{1}\dots {\text{d}}\phi _{n-2}{\text{d}}\phi _{n-1}{\text{d}}r={\frac {2\pi R^{n}}{n}}\cdot \prod _{k=2}^{n-1}\int _{0}^{\pi }(\sin(\phi _{n-k}))^{k-1}{\text{d}}\phi _{n-k}={\frac {2\pi R^{n}}{n}}\cdot \prod _{k=2}^{n-1}{\frac {{\sqrt {\pi }}\;\Gamma \left({\frac {k}{2}}\right)}{\Gamma \left({\frac {k+1}{2}}\right)}}={\frac {{\sqrt {\pi }}^{n}R^{n}}{\Gamma \left({\frac {n}{2}}+1\right)}}\quad n\geq 2$

این مربوط به حجم کروی یک $n$-بعدی hypersphere است:

$V_{n}(R)={\frac {{\sqrt {\pi }}^{n}R^{n}}{\Gamma \left({\frac {n}{2}}+1\right)}}$

مثال ها

2D:

$\int _{0}^{R}\int _{0}^{2\pi }r\mathrm {d} \phi _{1}\mathrm {d} r=\pi R^{2}$

3D:

$\int _{0}^{R}\int _{0}^{2\pi }\int _{0}^{\pi }r^{2}\sin(\phi _{2}){\text{d}}\phi _{2}{\text{d}}\phi _{1}{\text{d}}r={\frac {4\pi R^{3}}{3}}$

4D:

$\int _{0}^{R}\int _{0}^{2\pi }\int _{0}^{\pi }\int _{0}^{\pi }r^{3}\sin ^{2}(\phi _{1})\sin(\phi _{2}){\text{d}}\phi _{1}{\text{d}}\phi _{2}{\text{d}}\phi _{3}{\text{d}}r={\frac {\pi ^{2}R^{4}}{2}}$

مثال

تکلیف با استفاده از $n=3$ به عنوان مثال با محورهای مختصات مشترک $x,y,z$:

${\begin{aligned}x_{3}&=z=r\cos(\phi _{2})\\x_{2}&=x=r\sin(\phi _{2})\cos(\phi _{1})\\x_{1}&=y=r\sin(\phi _{2})\sin(\phi _{1})\\\end{aligned}}$

سپس زوایا عبارتند از:

${\begin{aligned}\tan(\phi _{2})={\frac {\left\Vert {\vec {L}}_{2}\right\Vert }{x_{3}}}&={\frac {\sqrt {x_{2}^{2}+x_{1}^{2}}}{x_{3}}}={\frac {\sqrt {x^{2}+y^{2}}}{z}}\\\tan(\phi _{1})={\frac {\left\Vert {\vec {L}}_{1}\right\Vert }{x_{2}}}&={\frac {\sqrt {x_{1}^{2}}}{x_{2}}}={\frac {y}{x}}\end{aligned}}$

جستارهای وابسته

• دستگاه مختصات خمیده خط
• دستگاه مختصات دکارتی
• دستگاه مختصات استوانه‌ای
• دستگاه مختصات قطبی
• کُره

منابع

• جورج براون آرفکن، روشهای ریاضی در فیزیک، ترجمهٔ اعظم پورقاضی، مرکز نشر دانشگاهی، شابک &#۸۲۰۶;۹۶۴-۰۱-۰۹۱۴-۲

• Wikipedia contributors, "Spherical coordinate system," Wikipedia, The Free Encyclopedia, http://en.wikipedia.org/w/index.php?title=Spherical_coordinate_system&oldid=172958916 (accessed November 22, 2007).