مختصات خمیدهخطی
در هندسه، دستگاه مختصات خمیدهخطی (به انگلیسی: Curvilinear Coordinates)، یک دستگاه مختصات در فضای اقلیدسی است که در آن، خطوط مختصات میتوانند خمیده باشند. دستگاههای مختصات دکارتی، استوانهای و کروی، نمونههایی خاص از دستگاه مختصات خمیدهخط هستند.
مختصات، اغلب برای تعریف مکان یا توزیع کمیتهای فیزیکی که ممکن است نردهای، برداری یا تانسوری باشند، بهکار میرود. بسته به کاربرد، ممکن است یک دستگاه مختصات خمیدهخط سادهتر از مختصات دکارتی باشد. برای مثال، یک مسئلهٔ فیزیکی با تقارن کروی در فضای R3 (مانند حرکت یک ذره در یک میدان)، در دستگاه مختصات کروی، آسانتر از دستگاه دکارتی حل میشود. دستگاه مختصات کروی، یکی از پرکاربردترین دستگاههای مختصات خمیدهخط در مباحثی مانند علوم زمین، نقشهنگاری، مهندسی و فیزیک (بهویژه مکانیک کوانتوم و نسبیت) بهشمار میرود.
دستگاه مختصات خمیدهخط، توصیفی کلی و یکپارچه از دستگاههای مختصات استاندارد ارائه میدهد. اصطلاحات عمومی حساب برداری و تانسورها مانند گرادیان، دیورژانس، کرل و عملگر لاپلاس برای مختصات خمیدهخط هم معتبرند.
دستگاه مختصات خمیدهخط متعامد در فضای سهبعدی
[ویرایش]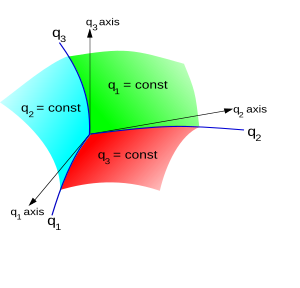
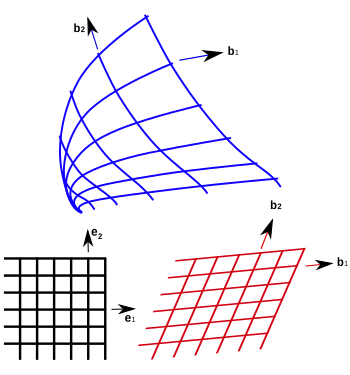
هر نقطه دلخواه p در فضای سهبعدی با استفاده از مختصات دکارتی به صورت یک سهتایی (x،y،z) نشان داده میشود. سطوح ثابت=x، ثابت=y و ثابت=z مسطح و عمود بر یکدیگرند؛ بنابراین از فصل مشترک این سه صفحه عمود برهم محورهای راستخط این دستگاه مختصات بدست میآیند. اکنون فرض کنید سه دسته سطح ثابت=q۱، ثابت=q۲ و ثابت=q۳ داشته باشید که این بار الزاماً عمود برهم یا مسطح نباشند، یعنی این سه دسته سطح میتوانند خمیده شکل بوده و عمود برهم نباشند. چون فصل مشترک سه دسته سطح q۱ و q۲ و q۳ با یکدیگر به صورت خطهای خمیده شکلاند، مختصات (q۱، q۲، q۳) را مختصات خمیدهخط مینامند.
ارتباط بین مختصات خمیدهخط و دکارتی، با استفاده از تبدیلهای وارونپذیر زیر برقرار میشود:
هر نقطه میتواند به صورت یک بردار مکان r در هر دستگاه مختصات نشان داده شود. برای دستگاه مختصات دکارتی:
که x, y, z مختصههای بردار مکان نسبت به بردارهای پایه ex, ey, ez هستند. بردارهای پایه مختصات دکارتی، پایه استاندارد بردارها هستند.
برای مختصات خمیدهخط، بردار مکان r به صورت زیر نوشته میشود:
که h1, h2, h3 ضرایب مقیاس بوده و نشاندهندهٔ تغییر شکل ایجادشده از مختصات دکارتی به مختصات خمیدهخط هستند و h1q1, h2q2, h3q3 مختصههای بردار مکان و b1, b2, b3 بردارهای پایه مختصات خمیدهخط هستند.
در دستگاه مختصات خمیدهخط، بردارهای پایه bi به مختصات qi وابسته بوده و لزوماً بر یکدیگر عمود نیستند. اگر این بردارهای پایه بر یکدیگر عمود باشند، پایه متعامد نامیده شده و دستگاه مختصات هم مختصات متعامد نامیده میشود. دستگاه خمیدهخط اجازه میدهد که بردارهای پایه بر یکدیگر عمود نبوده و طول آنها هم برابر واحد طول نباشد. یعنی بردارهای پایه در این دستگاه مختصات میتوانند اندازه و جهت دلخواه داشته باشند. استفاده از پایههای متعامد، محاسبات برداری را آسانتر میکند؛ ولی برخی موضوعات فیزیک و مهندسی، بهویژه مکانیک شارهها و مکانیک محیطهای پیوسته به بردارهای پایه نامتعامد نیاز دارند تا تغییر شکلها و جابجایی سیال را با در نظر گرفتن وابستگیهای جهتدار پیچیده کمیتهای فیزیکی توصیف کنند.
یک پایه که جهت و/یا اندازه بردارهایش از یک نقطه به نقطهٔ دیگر تغییر میکند، پایه موضعی نامیده میشود. بردارهای پایه مختصات خمیدهخط، موضعی هستند. بردارهای پایهای که در همه نقاط یکساناند، پایه سراسری نامیده شده و تنها در دستگاههای مختصات دکارتی و افاین مشاهده میشوند.
منابع
[ویرایش]- ریاضیفیزیک۱(رشته فیزیک)/ دکتر رحیم کوهیفایق و مهندس علیرضا بینش / دانشگاه پیامنور



