قضایای یکریختی
در ریاضیات، بخصوص در جبر مجرد، قضایای یکریختی (که به قضایای یکریختی نوتری نیز معروفند)، قضایایی اند که رابطه بین خارج قسمتها، همریختیها، و زیراشیاء را بیان می دارند. نسخههایی از قضایای یکریختی برای گروهها، حلقهها، فضاهای برداری، مدولها، جبرهای لی، و انواع دیگری از ساختارهای جبری به کار می روند. در جبر جهانی، قضایای یکریختی را می توان به جبرها و همنهشتیها نیز تعمیم داد.
گروه
[ویرایش]ابتدا قضایا یکریختی مربوط به گروهها را شرح میدهیم.
توضیحی در مورد اسامی و شماره قضایا
[ویرایش]در زیر چهار قضیه را با نامهای الف، ب، ج و د ارائه میکنیم. با این حال، توافق خاصی در مورد شماره گذاری وجود ندارد. در اینجا نمونههایی از قضایای یکریختی گروهها در این باب را ارائه می دهیم. توجه داشته باشید که این قضایا مشابه حلقهها و مدولها هستند.
| توضیحات | نویسنده | قضیه (الف) | قضیه (ب) | قضیه (ج) |
|---|---|---|---|---|
| بدون قضیه «سوم». | Jacobson[۱] | قضیه اساسی همریختی | قضیه دوم یکریختی | "عموما از آن به عنوان قضیه اول یکریختی یاد میشود." |
| van der Waerden,[۲] Durbin[۴] | قضیه اساسی همریختی | قضیه اول یکریختی | قضیه دوم یکریختی | |
| Knapp[۵] | بدون نام | قضیه دوم یکریختی | قضیه اول یکریختی | |
| Grillet[۶] | قضیه همریختی | قضیه دوم یکریختی | قضیه اول یکریختی | |
| قضایا سهگانه | (Other convention per Grillet) | قضیه اول یکریختی | قضیه سوم یکریختی | قضیه دوم یکریختی |
| Rotman[۷] | قضیه اول یکریختی | قضیه دوم یکریختی | قضیه سوم یکریختی | |
| Fraleigh[۸] | بدون نام | قضیه دوم یکریختی | قضیه سوم یکریختی | |
| Dummit & Foote[۹] | قضیه اول یکریختی | قضیه دوم یکریختی یا قضیه الماس یکریختی | قضیه سوم یکریختی | |
| بدون شمارهگذاری | Milne[۱۰] | قضیه همریختی | قضیه یکریختی | قضیه تناظر زیرگروهها |
| Scott[۱۱] | قضیه همریختی | قضیه یکریختی | قضیه تازهکار "Freshman" |
کمتر متداول است که قضیه (د)، که معمولاً به عنوان قضیه شبکه یا قضیه تناظر زیرگروهها شناخته می شود، در یکی از قضایای یکریختی قرار گیرد، اما زمانی که انجام می شود، آخرین مورد است.
صورت قضایا
[ویرایش]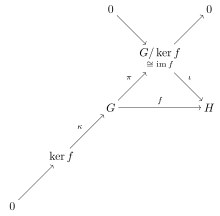
قضیه الف
[ویرایش]گروههای G و H مفروضند بطوری که f:G→H یک همریختی باشد. آنگاه:
- هسته f یک زیرگروه نرمال از G است.
- تصویر f یک زیرگروه از H است.
- تصویر f با گروه خارج قسمتی G/ker(f) یکریخت است.
به طور خاص اگر f پوشا باشد، آنگاه G/ker(f) با H یکریخت است.

قضیه ب
[ویرایش]اجازه دهید یک گروه باشد. بگذارید زیرگروهی از باشد، و فرض کنید یک زیرگروه عادی از باشد. آنگاه خواهیم داشت:
- حاصل ضرب زیرگروهی از است.
- اشتراک یک زیرگروه نرمال از است.
- گروههای خارجقسمتی و هم شکل هستند.
توجه شود، لزومی ندارد یک زیرگروه نرمال باشد، تا زمانی که زیرگروهی از نرمالساز در باشد. در این مورد، اشتراک یک زیرگروه نرمال از نیست، اما همچنان یک زیرگروهی نرمال از است.
این قضیه با اسامی قضیه یکریختی،[۱۳] قضیه الماس[۱۴] و لوزی[۱۲] شناخته میشود.
قضیه ج
[ویرایش]فرض کنید یک گروه و زیرگروه نرمالی از آن باشد. داریم:
- اگر یک زیرگروه از باشد بطوری که ، آنگاه شامل یک زیرگروه یکریخت با است.
- هر زیرگروه یکریخت با است بطوری که یک زیرگروه است که .
- اگر یک زیرگروه نرمال از باشد بطوری که ، آنگاه شامل یک زیرگروه نرمال یکریخت با است.
- هر زیرگروه نرمال یکریخت با است بطوری که یک زیرگروه نرمال است که .
- اگر یک زیرگروه نرمال از باشد بطوری که ، آنگاه گروه خارجقسمتی یکریخت با است.
قضیه د
[ویرایش]قضیه تناظر (همچنین به عنوان قضیه شبکه (lattice) شناخته می شود) گاهی اوقات قضیه یکریختی سوم یا چهارم نیز نامیده میشود.
لم زاسنهاوس (همچنین به عنوان لم پروانه شناخته می شود) گاهی اوقات قضیه چهارم یکریختی نامیده میشود.[۱۵]
حلقه
[ویرایش]این مقاله نیازمند ویکیسازی است. لطفاً با توجه به راهنمای ویرایش و شیوهنامه، محتوای آن را بهبود بخشید. |
ارجاعات
[ویرایش]- ↑ Jacobson (2009), sec 1.10
- ↑ van der Waerden, Algebra (1994).
- ↑ Durbin (2009), sec. 54
- ↑ [the names are] essentially the same as [van der Waerden 1994][۳]
- ↑ Knapp (2016), sec IV 2
- ↑ Grillet (2007), sec. I 5
- ↑ Rotman (2003), sec. 2.6
- ↑ Fraleigh (2003), Chap. 34
- ↑ Dummit, David Steven (2004). Abstract algebra. Richard M. Foote (Third ed.). Hoboken, NJ. pp. 97–98. ISBN 0-471-43334-9. OCLC 52559229.
- ↑ Milne (2013), Chap. 1, sec. Theorems concerning homomorphisms
- ↑ Scott (1964), secs 2.2 and 2.3
- ↑ ۱۲٫۰ ۱۲٫۱ Paul Moritz Cohn (2000). Classic Algebra. Wiley. p. 245. ISBN 978-0-471-87731-8.
- ↑ Milne (2013), Chap. 1, sec. Theorems concerning homomorphisms
- ↑ I. Martin Isaacs (1994). Algebra: A Graduate Course. American Mathematical Soc. p. 33. ISBN 978-0-8218-4799-2.
- ↑ Wilson, Robert A. (2009). The Finite Simple Groups. Graduate Texts in Mathematics 251. Springer-Verlag London. p. 7. doi:10.1007/978-1-84800-988-2. ISBN 978-1-4471-2527-3.
منابع
[ویرایش]- Emmy Noether, Abstrakter Aufbau der Idealtheorie in algebraischen Zahl- und Funktionenkörpern, Mathematische Annalen 96 (1927) pp. 26–61
- Colin McLarty, "Emmy Noether's 'Set Theoretic' Topology: From Dedekind to the rise of functors". The Architecture of Modern Mathematics: Essays in history and philosophy (edited by Jeremy Gray and José Ferreirós), Oxford University Press (2006) pp. 211–35.
- Jacobson, Nathan (2009), Basic algebra, vol. 1 (2nd ed.), Dover, ISBN 9780486471891
- Paul M. Cohn, Universal algebra, Chapter II.3 p. 57
- Milne, James S. (2013), Group Theory, 3.13
- van der Waerden, B. I. (1994), Algebra, vol. 1 (9 ed.), Springer-Verlag
- Dummit, David S.; Foote, Richard M. (2004). Abstract algebra. Hoboken, NJ: Wiley. ISBN 978-0-471-43334-7.
- Burris, Stanley; Sankappanavar, H. P. (2012). A Course in Universal Algebra (PDF). ISBN 978-0-9880552-0-9.
- W. R. Scott (1964), Group Theory, Prentice Hall
- John R. Durbin (2009). Modern Algebra: An Introduction (6 ed.). Wiley. ISBN 978-0-470-38443-5.
- Anthony W. Knapp (2016), Basic Algebra (Digital second ed.)
- Pierre Antoine Grillet (2007), Abstract Algebra (2 ed.), Springer
- Joseph J. Rotman (2003), Advanced Modern Algebra (2 ed.), Prentice Hall, ISBN 0130878685
- مشارکتکنندگان ویکیپدیا. «Isomorphism Theorems». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۱ مهٔ ۲۰۲۱.













