فهرست برخی گراف‌های خاص

این مقاله به معرفی و بیان خواص برخی گراف‌های خاص می‌پردازد. این گراف‌ها شامل گراف هی وود، گراف پترسن، گراف کنزر، گراف‌های $n$ -بعدی و ماز همپتون می‌باشند.

گراف هی وود

نامگذاری به نام: پرسی جان هیوود
تعداد رأس‌ها:۱۴
تعداد یال‌ها:۲۱
عدد رنگی:۲
اندیس رنگی:۳
مینیمم طول دور:۶
منتظم

گراف هی وود یک گراف بدون جهت با14 رأس و 21 یال است .

گراف هی وود ۳-منتظم است و این یعنی از هر راس آن سه یال بیرون آمده است، و همهٔ دورها در آن حداقل 6 و حد اکثر 14 یال دارد . عدد تقاطع گراف 3 است و کوچکترین گراف منتظم با این عدد تقاطع است. این گراف به نام پرسی جان هی وود نامگذاری شده‌است.

این گراف را هم به صورت دایره مانند می‌توان مشاهده نمود و هم به صورت بیضی مانند، در درون این گراف هر جفت از رأس‌هایش که به هم متصل اند در میانشان چهار راس وجود دارد و به تعداد راس‌هایش در داخل خود مثلث به وجود آورده‌است .

گراف پترسن

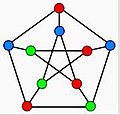
گراف پترسن یک گراف بدون جهت با ۱۰ رأس و ۱۵ یال است. گرافی کوچک که مثال و مثال نقض مفیدی برای خیلی از مسائل در نظریه گراف است. این گراف به جولیوس پترسن نسبت داده شده ولی در حقیقت برای اولین بار، ۱۲ سال زودتر در سال ۱۸۸۶ به وجود آمده بود.

نامگذاری به نام: جولیوس پترسن
تعداد رأس‌ها:10
تعداد یال‌ها: 15
قطر:2
مینیمم طول دور:5
عدد رنگی:۳
اندیس رنگی:۴
منتظم
غیرمسطح
عدد تقاطع گراف پترسن 2 است.
گراف پترسن در صفحه می‌تواند به گونه‌ای رسم شود که طول هر یال برابر واحد باشد
گراف پترسن شبه هامیلتونی است.
عدد رنگی گراف پترسن 3 است. یک نمونه رنگ آمیزی با 3 رنگ.

ساخت

گراف پترسن، گراف مکمل گراف خط $K_{5}$ است. همچنین گراف کنزر $KG_{5,2}$ است به این معنا که اگر برای هر کدام از زیرمجموعه‌های دو عضوی یک مجموعهٔ ۵ عضوی یک رأس در نظر بگیریم و بین هر دو رأسی که زیرمجموعه‌ها ی نظیرشان ناسازگار باشند یک یال وصل کنیم، گراف پترسن ساخته می‌شود.
گراف پترسن هم با گراف کامل $K_{5}$ و هم با گراف دوبخشی کامل $K_{3,3}$ همومورف است.
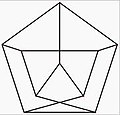
متداول‌ترین شیوهٔ رسم گراف پترسن در یک صفحه، یک پنج ضلعی با یک ستارهٔ پنج رأسی درون آن است که هر یک از رأس‌های ستاره به رأس‌های پنج ضلعی با یک یال وصل می‌شود.این شیوهٔ نمایش متقارن است. در این شکل یال‌ها در ۵ نقطه یکدیگر را قطع می‌کنند.(شکل۱) این روش ترسیم بهترین روش برای مینیمم کردن تعداد تقاطع‌ها نیست. روشی دیگر برای کشیدن گراف پترسن با دو نقطهٔ تقاطع وجود دارد که در شکل۲ نشان داده شده‌است. بنابراین عدد تقاطع گراف پترسن ۲ است.
گراف پترسن همچنین می‌تواند در صفحه به گونه‌ای رسم شود که همهٔ یال‌ها طول یکسان برابر واحد داشته باشند.(شکل۳)

مسیرها و دورهای همیلتونی

گراف پترسن مسیر هامیلتونی دارد ولی دور هامیلتونی ندارد. گراف پترسن کوچکترین گراف شبه هامیلتونی است یعنی اگرچه دور هامیلتونی ندارد، هر کدام از رأس‌هایش که حذف شوند می‌توان یک دور هامیلتونی در آن پیدا کرد.(شکل۴)

گراف نسر(Kneser)

در نظریه گراف گراف نسر، $KG_{n,k}$ ، گرافی است که رأس‌های آن نظیر زیرمجموعه‌های k عضوی از یک مجموعه ی n عضوی است. بین دو رأس یک یال وجود دارد اگر و تنها اگر زیرمجموعه‌های نظیر رأس‌ها ناسازگار باشند(اشتراکشان تهی باشد). این گراف‌ها به نام مارتین کنزر نامگذاری شده‌اند که برای اولین بار آن‌ها را در سال ۱۹۵۵ بررسی کرد.

مثال‌ها

گراف کامل n رأسی گراف نسر $KG_{n,1}$ است.
گراف $KG_{5,2}$ با گراف پترسن ایزومورف است.

خصوصیات

در گراف نسر هر رأس با انتخاب k از n-k رأس دیگر مجاور است.
همانگونه که نسر حدس زد عدد رنگی گراف $KG_{n,k}$ دقیقاً برابر n-۲k+۲ است. Lovasz در سال ۱۹۷۸ و Joshua در سال ۲۰۰۲ برای این فرمول اثبات‌هایی توپولوژیکی ارائه دادند. در سال ۲۰۰۴ Matoušek اثباتی کاملاً ترکیبیاتی برای آن پیدا کرد.
وقتی n بزرگتر مساوی ۳k باشد گراف نسر همیشه دور هامیلتونی خواهد داشت (چن ۲۰۰۰). محاسبات نشان داده‌اند که همهٔ گراف‌های همبند کنزر با n‌های کوچکتر مساوی ۲۷ به جز گراف پترسن، همیلتونی هستند.
اگر n کوچکتر از ۳k باشد گراف نسر هیچ مثلثی نخواهد داشت.

گراف‌های n- بعدی

مکعب‌ها با ابعاد مختلف می‌توانند گراف در نظر گرفته شوند. مکعب با بعد n را با $Q_{n}$ نشان می‌دهیم. کد گری کدی است که هر کد با کد قبلی فقط در یک بیت تفاوت دارد و کد آخر با کد اول نیز در یک بیت متفاوت است. می‌توانیم این مسئله را با استفاده از $Q_{n}$ حل کنیم. هر کدگری دور هامیلتونی در $Q_{n}$ است. می‌توانیم $Q_{n}$ را از روی $Q_{n-1}$ بسازیم. ابتدا یک کپی از $Q_{n-1}$ رسم می‌کنیم( $P_{n-1}$ ). ابتدای بیت‌های $Q_{n-1}$ ، صفر و ابتدای بیت‌های
$P_{n-1}$ ، یک می‌گذاریم. سپس رأس‌های متناظر $Q_{n-1}$ و $P_{n-1}$ را به هم وصل می‌کنیم.

سفیروت

درخت زندگی سمبل اصلی آئین کابالا است. در شکل رأس‌ها، ۱۰ سفیروت (مظهر خدایی) را نمایش می‌دهند(به عقیدهٔ Zohar، جهان در ده کلمه خلق شده‌است). ۲۲ یال(برابر ۲۲ تا حرف عبری کانال‌هایی هستند که نیروهای یزدانی از نیان آن‌ها عبور می‌کنند.) این شکل به‌طور عمده بدنهٔ جهان یا نقشه خلقت را نشان می‌دهد.

ماز همپتون

هر مازی نظیر یک گراف است. رأس‌ها را محل‌های تقاطع راه‌ها، و یال‌ها را معادل مسیرها در نظر می‌گیریم. قدیمی‌ترین ماز باقی مانده در بریتانیا در قصر همپتون قرار دارد. قابلیت عبور از مازها یک زمانی مسئلهٔ مهمی بود. سؤال این است که آیا الگوریتمی وجود دارد که کسی بتواند بدون آنکه از قبل ساختار ماز را بداند، از ماز عبور کند و از هر مسیر دو بار در جهت مخالف عبور کند؟ اولین الگوریتم برای عبور از یک ماز به C.Wiener نسبت داده شده‌است. Tremaux الگوریتمی بهینه تر در سال ۱۸۸۲ ارائه داد. ساده‌ترین و بهترین الگوریتم را Tarry در سال ۱۸۹۵ پیشنهاد داد.

منابع