فاکتور پرتی محلی

در تشخیص ناهنجاری، فاکتور پَرتی محلی یا انزوای محلی (LOF) الگوریتمی است که توسط Markus M. Breunig , Hans-Peter Kriegel , Raymond T. Ng و Jörg Sander در سال ۲۰۰۰ برای یافتن نقاط داده‌های نابه هنجار یا غیرمعمول توسط اندازه‌گیری انحراف محلی یک داده نسبت به همسایگان آن نقطه ارائه شده‌است^[۱]

LOF دارای برخی مفاهیم مشترک با DBSCAN و OPTICS است که به عنوان مثال می‌توان از مفاهیم "فاصله هسته" و "فاصله قابل دسترسی (reachability distance)" که برای تخمین تراکم محلی (چگالی محلی) از آن استفاده می‌شود، نام برد.^[۲]

ایده پایه

فاکتور پَرتی محلی یا دور افتادگی محلی بر اساس مفهومی از تراکم محلی پایه‌گذاری شده‌است، جایی که محلی بودن نقطه توسط k تا از نزدیکترین نقطه‌های همسایه ارائه می‌شود، که فاصله آنها برای تخمین زدن تراکم استفاده می‌شود. با مقایسه تراکم محلی یک شی با تراکم محلی همسایگان آن، می‌توان مناطقی با چگالی مشابه و نقاطی را که به مراتب چگالی پایین‌تر از همسایگان خود دارند؛ شناسایی کرد. این نقاط به عنوان نقاط پرت محسوب می‌شوند.

تراکم محلی را با فاصله معمول ای که توسط آن می‌توان از همسایگان خود به یک نقطه «رسید» تخمین زده می‌شود.

تعریف «فاصله قابل دستیابی» مورد استفاده در LOF معیار دیگری برای تولید نتایج پایدارتر در خوشه‌ها است. «فاصله دستیابی» که توسط LOF استفاده می‌شود دارای برخی جزئیات ظریف است که اغلب در منابع ثانویه نادرست پیدا می‌شود مانند کتاب درسی آیثم آلپایدین.^[۳]

تعریف رسمی

اگر $k -distance(A)$ فاصله شی A تا k امین نزدیکترین همسایه باشد. (توجه داشته باشید که مجموعه k نزدیکترین همسایگان شامل تمامی اشیای در این فاصله است که در حالت «تساوی» می‌تواند بیش از k شی باشد) مجموعه k نزدیکترین همسایگان را به عنوان $N k (A)$ مشخص می‌کنیم.

تصویر فاصله قابل دسترسی اجسام B و C فاصله قابلیت دسترسی یکسانی دارند ( $k=۳$ )، در حالی که $D$ نزدیکترین همسایه *k نیست*

این فاصله برای تعریف آنچه که از آن به عنوان فاصله قابلیت دسترسی نام برده می‌شود استفاده می‌شود:

$reachability-distance k (A, B)=max{k -distance(B), d(A, B)}$

به‌طور توصیفی، فاصله قابلیت دسترسی (reachability distance) جسم A از B، فاصله واقعی دو جسم است، اما حداقل $k -distance$ متعلق به B است. اشیاء ایی که متعلق به k نزدیکترین همسایگان B هستند

(«هسته» متعلق به B، و تجزیه و تحلیل خوشه DBSCAN را بررسی کنید) در نظر گرفته می‌شود که به اندازه یکسان از B دور هستند.

دلیل این فاصله دستیابی به پاسخ‌های پایدارتر است

توجه داشته باشید که این فاصله در تعریف ریاضی نیست، زیرا که متقارن نیست. (اگرچه استفاده از $k -distance(A)$ یک اشتباه معمول است^[۴]) اما این یک روش کمی متفاوت تر است که از آن به عنوان LOF ساده نام برده می‌شود

تراکم قابل دسترسی محلی (چگالی قابل دسترسی محلی) یک جسم A به این ترتیب تعریف می‌شود

$lrdk(A):=۱/(.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}ΣB ∈ Nk(A)reachability-distancek(A, B)/|Nk(A)|)$

که معکوس میانگین فاصله قابل دسترسی شی A از همسایگان آن است. توجه داشته باشید که میانگین قابلیت دسترسی همسایگان از A نیست (میانگین قابلیت دسترسی طبق تعریف $k -distance(A)$ می‌باشد)، بلکه فاصله ای است که از همسایگان A می‌توان به A رسید.

که با نقطه‌های تکراری، این مقدار امکان دارد بی‌نهایت شود.

سپس تراکم قابلیت دسترسی محلی با تراکم همسایگان توسط فرمول زیر مقایسه می‌شود

$LOF k (A):= Σ B \in N k (A) lrd k (B) / lrd k (A) / |N k (A)| = Σ B \in N k (A) lrd k (B) / |N k (A)| \cdot lrd k (A)$

که میانگین تراکم قابلیت دسترسی(local reachability density) محلی همسایگان تقسیم بر تراکم قابلیت دسترسی محلی خود جسم است.

مقدار تقریبی $۱$ نشان می‌دهد که این جسم با همسایگان خود قابل مقایسه است (و بنابراین جسمی غیر پَرت است). مقدار زیر $۱$ نشانگر یک منطقه متراکم تر است (که یک مقدار نزدیک و غیر پَرت است)، در حالی که مقادیر به‌طور قابل توجهی بزرگتر از $۱$ نشان دهنده پَرت بودن است.

$LOF(k) ~ ۱$ به معنای تراکم (چگالی) مشابه با همسایگان است,

$LOF(k) <1$ یه معنای تراکم بیشتر از همسایگان است (Inlier، غیر پَرت),

$LOF(k)> 1$ به معنای چگالی کمتر از همسایگان است (Outlier و پرت بودن)

مزایا

امتیازات LOF همان‌طور که توسط ELKI تجسم شده‌است. در حالی که خوشه فوقانی سمت راست دارای تراکم قابل مقایسه با نقاط پرت نزدیک به خوشه پایین سمت چپ است، اما آنها به درستی شناسایی می‌شوند.

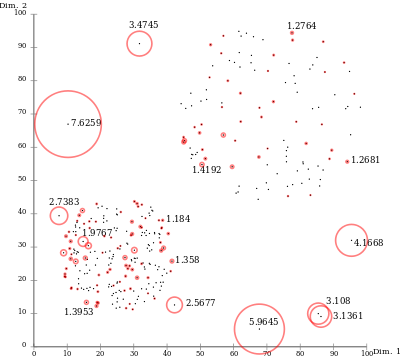
به خاطر رویکرد محلی الگوریتم، LOF قادر است تا نقاط پرتی را در یک مجموعه داده شناسایی کند که به‌طور عادی در منطقه دیگری از آن مجموعه داده پَرت حساب نخواهد شد.

به عنوان مثال، یک نقطه در یک فاصله کم از یک خوشه بسیار متراکم یک نقطه پَرت است، در حالی که یک نقطه در درون یک خوشه پراکنده ممکن است مسافت‌های یکسان و مشابه ایی با همسایگان خود را نشان دهد.

در حالی که شهود هندسی LOF فقط برای فضاهای برداری با ابعاد کم کاربرد دارد، می‌توان این الگوریتم را در هر زمینه ای که توانایی تعریف یک تابع عدم تشابه وجود داشته باشد اعمال کرد.

به‌طور تجربی نشان داده شده‌است که در وضعیت‌های متعدد بسیار خوب عمل می‌کند، و اغلب عملکرد به مراتب بهتری از رقبایش دارد، به عنوان مثال می‌توان از تشخیص نفوذ شبکه^[۵] و طبقه‌بندی داده‌های معیار پردازش شده نام برد.^[۶]

خانواده متدهای LOF را می‌توان به راحتی تعمیم داد و سپس آنها را برای مشکلات متفاوت اعمال کرد که به‌طور مثال می‌توان از شناسایی نقاط دور یا پرت در داده‌های جغرافیایی یا استریم‌های ویدویی نام برد.^[۷]

معایب و اکستنشن‌ها

مقادیر حاصل در واقع به نسبت پاسخ‌های مطلوب به نامطلوب هستند (quotient-values) که تفسیر آنها دشوار است. مقدار ۱ یا حتی کمتر نشان دهنده یک مقدار نزدیک و غیر پرت (inlier) واضح است، اما هیچ قانون مشخصی برای زمانی که یک نقطه پَرت و دور است وجود ندارد. به‌طور مثال:

در یک مجموعه داده، مقدار ۱٫۱ ممکن است پَرت و دور باشد، اما در مجموعه داده دیگر و پارامتر سازی متفاوت (با نوسانات محلی شدید) مقدار ۲ می‌تواند یک مقدار نزدیک و غیر پَرت باشد. همچنین این تفاوت‌ها به دلیل محلی بودن رویکرد الگوریتم می‌توانند در یک مجموعه داده رخ دهند.

برای حل مشکلات اکستنشن‌های LOF ای وجود دارد که سعی در بهبود بیشتر LOF در این جنبه‌ها دارد:

Feature Bagging for Outlier Detection^[۸] الگوریتم را در چندین پیش‌بینی اجرا می‌کند و نتایج را برای بهبود کیفیت تشخیص در ابعاد بالا ترکیب می‌کند. این اولین رویکرد یادگیری گروه برای تشخیص دور است، برای سایر گزینه‌ها به رجوع شود.^[۹]
احتمال پرتی محلی (LoOP)^[۱۰] روشی است که از LOF مشتق شده اما با استفاده از آمار محلی ارزان قیمت نسبت به انتخاب پارامتر k حساسیت کمتری پیدا می‌کند. بعلاوه، مقادیر بدست آمده در محدوده مقداری $[۰:۱]$ مقیاس بندی می‌شوند.
تفسیر و یکپارچه سازی امتیازات دور از انتظار^[۱۱] یک عادی سازی نمره‌های دور افتاده LOF را به فاصله $[۰:۱]$ با استفاده از مقیاس سازی آماری برای افزایش قابلیت استفاده پیشنهاد می‌کند و می‌توان نسخه بهبود یافته ایده‌های (LoOP) را مشاهده کرد.
در ارزیابی رتبه‌بندی Outlier و امتیازات Outlier^[۱۲] روشهایی را برای اندازه‌گیری شباهت و تنوع روشها برای ساخت گروه‌های پیشرفته تشخیص خارج از خانه با استفاده از انواع LOF و الگوریتم‌های دیگر و بهبود رویکرد Feature Bagging که در بالا بحث شد، پیشنهاد می‌کند.
بازنگری شناسایی پَرتی محلی : یک دیدگاه کلی در مورد مکان با برنامه‌های کاربردی برای شناسایی فضایی، ویدئویی و شبکه^[۱۳] مورد الگوی کلی در روش‌های مختلف شناسایی محلی دوردست (از جمله، به عنوان مثال، LOF، یک نسخه ساده از LOF و LoOP) و چکیده از این به یک چارچوب کلی است. این چارچوب سپس به عنوان مثال، برای شناسایی نقاط دور در داده‌های جغرافیایی، جریان‌های ویدئویی و شبکه‌های تألیف اعمال می‌شود.

منابع

↑ Breunig, M. M. ; Kriegel, H. -P. ; Ng, R. T. ; Sander, J. (2000). LOF: Identifying Density-based Local Outliers (PDF). Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data. SIGMOD. pp. 93–104. doi:10.1145/335191.335388. ISBN 1-58113-217-4.
↑ Breunig, M. M. ; Kriegel, H. -P. ; Ng, R. T. ; Sander, J. R. (1999). "OPTICS-OF: Identifying Local Outliers" (PDF). Principles of Data Mining and Knowledge Discovery. Lecture Notes in Computer Science. 1704. p. 262. doi:10.1007/978-3-540-48247-5_28. ISBN 978-3-540-66490-1.
↑ Alpaydin, Ethem (2020). Introduction to machine learning (Fourth ed.). Cambridge, Massachusetts. ISBN 978-0-262-04379-3. OCLC 1108782604.
↑ Schubert, E.; Zimek, A.; Kriegel, H. -P. (2012). "Local outlier detection reconsidered: A generalized view on locality with applications to spatial, video, and network outlier detection". Data Mining and Knowledge Discovery. 28: 190–237. doi:10.1007/s10618-012-0300-z.
↑ Lazarevic, A. ; Ozgur, A. ; Ertoz, L. ; Srivastava, J. ; Kumar, V. (2003). "A comparative study of anomaly detection schemes in network intrusion detection" (PDF). Proc. 3rd SIAM International Conference on Data Mining: 25–36. Archived from the original (PDF) on 2013-07-17. Retrieved 2010-05-14.{{cite journal}}: نگهداری یادکرد:نام‌های متعدد:فهرست نویسندگان (link)
↑ Campos, Guilherme O.; Zimek, Arthur; Sander, Jörg; Campello, Ricardo J. G. B.; Micenková, Barbora; Schubert, Erich; Assent, Ira; Houle, Michael E. (2016). "On the evaluation of unsupervised outlier detection: measures, datasets, and an empirical study". Data Mining and Knowledge Discovery. 30 (4): 891–927. doi:10.1007/s10618-015-0444-8. ISSN 1384-5810.
↑ Schubert, E.; Zimek, A.; Kriegel, H. -P. (2012). "Local outlier detection reconsidered: A generalized view on locality with applications to spatial, video, and network outlier detection". Data Mining and Knowledge Discovery. 28: 190–237. doi:10.1007/s10618-012-0300-z.
↑ Lazarevic, A.; Kumar, V. (2005). "Feature bagging for outlier detection". Proc. 11th ACM SIGKDD International Conference on Knowledge Discovery in Data Mining: 157–166. doi:10.1145/1081870.1081891. ISBN 1-59593-135-X.
↑ Zimek, A.; Campello, R. J. G. B.; Sander, J. R. (2014). "Ensembles for unsupervised outlier detection". ACM SIGKDD Explorations Newsletter. 15: 11–22. doi:10.1145/2594473.2594476.
↑ Kriegel, H. -P. ; Kröger, P. ; Schubert, E. ; Zimek, A. (2009). LoOP: Local Outlier Probabilities (PDF). Proceedings of the 18th ACM Conference on Information and Knowledge Management. CIKM '09. pp. 1649–1652. doi:10.1145/1645953.1646195. ISBN 978-1-60558-512-3.
↑ Kriegel, H. P. ; Kröger, P. ; Schubert, E. ; Zimek, A. (2011). Interpreting and Unifying Outlier Scores. Proceedings of the 2011 SIAM International Conference on Data Mining. pp. 13–24. CiteSeerX 10.1.1.232.2719. doi:10.1137/1.9781611972818.2. ISBN 978-0-89871-992-5.
↑ Schubert, E. ; Wojdanowski, R. ; Zimek, A. ; Kriegel, H. P. (2012). On Evaluation of Outlier Rankings and Outlier Scores. Proceedings of the 2012 SIAM International Conference on Data Mining. pp. 1047–1058. CiteSeerX 10.1.1.300.7205. doi:10.1137/1.9781611972825.90. ISBN 978-1-61197-232-0.
↑ Schubert, E.; Zimek, A.; Kriegel, H. -P. (2012). "Local outlier detection reconsidered: A generalized view on locality with applications to spatial, video, and network outlier detection". Data Mining and Knowledge Discovery. 28: 190–237. doi:10.1007/s10618-012-0300-z.

[1] Breunig, M. M. ; Kriegel, H. -P. ; Ng, R. T. ; Sander, J. (2000). LOF: Identifying Density-based Local Outliers (PDF). Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data. SIGMOD. pp. 93–104. doi:10.1145/335191.335388. ISBN 1-58113-217-4.

[2] Breunig, M. M. ; Kriegel, H. -P. ; Ng, R. T. ; Sander, J. R. (1999). "OPTICS-OF: Identifying Local Outliers" (PDF). Principles of Data Mining and Knowledge Discovery. Lecture Notes in Computer Science. 1704. p. 262. doi:10.1007/978-3-540-48247-5_28. ISBN 978-3-540-66490-1.

[3] Alpaydin, Ethem (2020). Introduction to machine learning (Fourth ed.). Cambridge, Massachusetts. ISBN 978-0-262-04379-3. OCLC 1108782604.

[4] Schubert, E.; Zimek, A.; Kriegel, H. -P. (2012). "Local outlier detection reconsidered: A generalized view on locality with applications to spatial, video, and network outlier detection". Data Mining and Knowledge Discovery. 28: 190–237. doi:10.1007/s10618-012-0300-z.

[5] Lazarevic, A. ; Ozgur, A. ; Ertoz, L. ; Srivastava, J. ; Kumar, V. (2003). "A comparative study of anomaly detection schemes in network intrusion detection" (PDF). Proc. 3rd SIAM International Conference on Data Mining: 25–36. Archived from the original (PDF) on 2013-07-17. Retrieved 2010-05-14.{{cite journal}}: نگهداری یادکرد:نام‌های متعدد:فهرست نویسندگان (link)

[CamposZimek2016-6] Campos, Guilherme O.; Zimek, Arthur; Sander, Jörg; Campello, Ricardo J. G. B.; Micenková, Barbora; Schubert, Erich; Assent, Ira; Houle, Michael E. (2016). "On the evaluation of unsupervised outlier detection: measures, datasets, and an empirical study". Data Mining and Knowledge Discovery. 30 (4): 891–927. doi:10.1007/s10618-015-0444-8. ISSN 1384-5810.

[7] Schubert, E.; Zimek, A.; Kriegel, H. -P. (2012). "Local outlier detection reconsidered: A generalized view on locality with applications to spatial, video, and network outlier detection". Data Mining and Knowledge Discovery. 28: 190–237. doi:10.1007/s10618-012-0300-z.

[8] Lazarevic, A.; Kumar, V. (2005). "Feature bagging for outlier detection". Proc. 11th ACM SIGKDD International Conference on Knowledge Discovery in Data Mining: 157–166. doi:10.1145/1081870.1081891. ISBN 1-59593-135-X.

[9] Zimek, A.; Campello, R. J. G. B.; Sander, J. R. (2014). "Ensembles for unsupervised outlier detection". ACM SIGKDD Explorations Newsletter. 15: 11–22. doi:10.1145/2594473.2594476.

[10] Kriegel, H. -P. ; Kröger, P. ; Schubert, E. ; Zimek, A. (2009). LoOP: Local Outlier Probabilities (PDF). Proceedings of the 18th ACM Conference on Information and Knowledge Management. CIKM '09. pp. 1649–1652. doi:10.1145/1645953.1646195. ISBN 978-1-60558-512-3.

[11] Kriegel, H. P. ; Kröger, P. ; Schubert, E. ; Zimek, A. (2011). Interpreting and Unifying Outlier Scores. Proceedings of the 2011 SIAM International Conference on Data Mining. pp. 13–24. CiteSeerX 10.1.1.232.2719. doi:10.1137/1.9781611972818.2. ISBN 978-0-89871-992-5.

[12] Schubert, E. ; Wojdanowski, R. ; Zimek, A. ; Kriegel, H. P. (2012). On Evaluation of Outlier Rankings and Outlier Scores. Proceedings of the 2012 SIAM International Conference on Data Mining. pp. 1047–1058. CiteSeerX 10.1.1.300.7205. doi:10.1137/1.9781611972825.90. ISBN 978-1-61197-232-0.

[generalized-13] Schubert, E.; Zimek, A.; Kriegel, H. -P. (2012). "Local outlier detection reconsidered: A generalized view on locality with applications to spatial, video, and network outlier detection". Data Mining and Knowledge Discovery. 28: 190–237. doi:10.1007/s10618-012-0300-z.

[۱]

[۲]

[۳]

[۴]

[۵]

[۶]

[۷]

[۸]

[۹]

[۱۰]

[۱۱]

[۱۲]

[۱۳]