ضریب شدت تنش

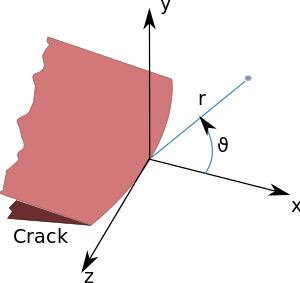
مختصات قطبی در نوک ترک.

ضریب شدت تنش، $K$، در مکانیک شکست برای پیش بینی وضعیت تنش (شدت تنش) در نزدیکی نوک ترک یا شکاف ناشی از بار از راه دور یا تنش‌های پسماند به کار می‌رود. ضریب شدت تنش یک ساختهٔ نظری است که معمولاً برای یک ماده الاستیک خطی و همگن اعمال می شود و به عنوان یک معیار شکست برای مواد ترد استفاده می‌شود. همچنین یک تکنیک مهم در مبحث حد مجاز آسیب است. این مفهوم همچنین برای موادی که تسلیم در مقیاس کوچک در نوک ترک دارند می‌تواند به کار رود.

بزرگی $K$ به هندسه نمونه، اندازه و محل ترک یا شکاف، و بزرگی و توزیع بار روی ماده بستگی دارد.که می توان آن را به صورت زیر نوشت:

$$K=\sigma {\sqrt {\pi a}}\,f(a/W)$$

که $f(a/W)$ تابعی از طول ترک، $a$، و عرض نمونه، $W$، و تنش اعمال شده،$\sigma$ ، است که وابسته به هندسه نمونه می‌باشد.

تئوری الاستیک خطی پیش‌بینی می‌کند که توزیع تنش ($\sigma _{ij}$) نزدیک نوک ترک، در مختصات قطبی ( $r,\theta$ ) با مبدأ نوک ترک، به شکل زیر است

$\sigma _{ij}(r,\theta )={\frac {K}{\sqrt {2\pi r}}}\,f_{ij}(\theta )+\,\,{\rm {higher\,order\,terms}}$

که $K$ ضریب شدت تنش است (با واحد تنش $\times$ طول ^1/2 ) و $f_{ij}$ یک کمیت بدون بعد است که با بارگذاری و هندسه تغییر می کند. از لحاظ نظری، هنگامی که $r$ به سمت 0 می‌رود، استرس $\sigma _{ij}$ به سمت $\infty$ می‌رود و منجر به تکین شدن استرس می شود. با این حال، در عمل، این رابطه در نزدیکی نوک ($r$ کوچک) برقرار نیست. زیرا پلاستیسیته در تنش‌های بیشتر از استحکام تسلیم ماده رخ می‌دهد و روش الاستیک خطی کارایی خود را از دست می‌دهد. با این وجود، اگر ناحیه پلاستیک نوک ترک در مقایسه با طول ترک کوچک باشد، توزیع تنش مجانبی در نزدیکی نوک ترک همچنان قابل اعمال است.

ضریب شدت تنش برای حالت‌های مختلف

حالت I، حالت II و حالت III در بارگذاری ترک.

در سال 1957، جی. اروین دریافت که تنش‌های اطراف ترک را می‌توان بر حسب یک عامل مقیاس به نام ضریب شدت تنش بیان کرد . او دریافت که یک ترک تحت هر بارگذاری دلخواه می تواند به سه نوع حالت مستقل خطی تجزیه شود. این نوع بارگذاری‌ها همانطور که در شکل نشان داده شده است با عنوان حالت‌های I یا II یا III طبقه‌بندی می‌شوند. حالت I یک حالت باز‌شونده (کششی) است که در آن سطوح ترک مستقیماً از هم جدا می شوند. حالت II یک حالت لغزشی ( برشی درون صفحه) است که در آن سطوح ترک بر روی یکدیگر در جهت عمود بر لبه جلویی ترک می‌لغزند. حالت III حالت پارگی (برشی برون صفحه) است که در آن سطوح ترک نسبت به یکدیگر و موازی با لبه جلویی ترک، حرکت می کنند. حالت I رایج ترین نوع بارگذاری است که در طراحی مهندسی با آن مواجه می‌شویم.

پایین‌نویس‌های مختلفی برای تمایز ضریب شدت تنش برای سه حالت مختلف استفاده می‌شود. ضریب شدت تنش برای حالت I، $K_{\rm {I}}$ تعیین شده است و در حالت باز شدن ترک استفاده می‌شود. ضریب شدت تنش حالت II، $K_{\rm {II}}$، برای حالت لغزش ترک و ضریب شدت تنش حالت III، $K_{\rm {III}}$، برای حالت پارگی استفاده می‌شود. این عوامل به این صورت تعریف می شوند:

${\begin{aligned}K_{\rm {I}}&=\lim _{r\rightarrow 0}{\sqrt {2\pi r}}\,\sigma _{yy}(r,0)\\K_{\rm {II}}&=\lim _{r\rightarrow 0}{\sqrt {2\pi r}}\,\sigma _{yx}(r,0)\\K_{\rm {III}}&=\lim _{r\rightarrow 0}{\sqrt {2\pi r}}\,\sigma _{yz}(r,0)\,.\end{aligned}}$

معادلات میدان برای میدان‌های تنش و جابجایی

میدان تنش حالت I بیان شده بر حسب $K_{\rm {I}}$ $\left\{{\begin{aligned}\sigma _{xx}\\\sigma _{yy}\\\sigma _{xy}\end{aligned}}\right\}={\frac {K_{\rm {I}}}{\sqrt {2\pi r}}}\cos {\frac {\theta }{2}}\left\{{\begin{aligned}1-\sin {\frac {\theta }{2}}\sin {\frac {3\theta }{2}}\\1+\sin {\frac {\theta }{2}}\sin {\frac {3\theta }{2}}\\\sin {\frac {\theta }{2}}\cos {\frac {3\theta }{2}}\end{aligned}}\right\}$, است. و $\left\{{\begin{aligned}\sigma _{rr}\\\sigma _{\theta \theta }\\\sigma _{r\theta }\end{aligned}}\right\}={\frac {K_{\rm {I}}}{\sqrt {2\pi r}}}\cos {\frac {\theta }{2}}\left\{{\begin{aligned}1+\sin ^{2}{\frac {\theta }{2}}\\\cos ^{2}{\frac {\theta }{2}}\\\sin {\frac {\theta }{2}}\cos {\frac {\theta }{2}}\end{aligned}}\right\}$. $\sigma _{zz}=\nu _{1}(\sigma _{xx}+\sigma _{yy})=\nu _{1}(\sigma _{rr}+\sigma _{\theta \theta })$, $\sigma _{xz}=\sigma _{yz}=\sigma _{rz}=\sigma _{\theta z}=0$. جابجایی‌ها $\left\{{\begin{aligned}u_{x}\\u_{y}\end{aligned}}\right\}={\frac {K_{\rm {I}}}{2E}}{\sqrt {\frac {r}{2\pi }}}\left\{{\begin{aligned}(1+\nu )\left[(2\kappa -1)\cos {\frac {\theta }{2}}-\cos {\frac {3\theta }{2}}\right]\\(1+\nu )\left[(2\kappa +1)\sin {\frac {\theta }{2}}-\sin {\frac {3\theta }{2}}\right]\end{aligned}}\right\}$ $\left\{{\begin{aligned}u_{r}\\u_{\theta }\end{aligned}}\right\}={\frac {K_{\rm {I}}}{2E}}{\sqrt {\frac {r}{2\pi }}}\left\{{\begin{aligned}(1+\nu )\left[(2\kappa -1)\cos {\frac {\theta }{2}}-\cos {\frac {3\theta }{2}}\right]\\(1+\nu )\left[-(2\kappa +1)\sin {\frac {\theta }{2}}+\sin {\frac {3\theta }{2}}\right]\end{aligned}}\right\}$ $u_{z}=-\left({\frac {\nu _{2}z}{E}}\right)(\sigma _{xx}+\sigma _{yy})=-\left({\frac {\nu _{2}z}{E}}\right)(\sigma _{rr}+\sigma _{\theta \theta })$ هستند که برای شرایط تنش صفحه‌ای $\kappa ={\frac {(3-\nu )}{(1+\nu )}}$, $\nu _{1}=0$, $\nu _{2}=\nu$, و برای کرنش صفحه‌ای $\kappa =(3-4\nu )$, $\nu _{1}=\nu$, $\nu _{2}=0$. برای حالت II $\left\{{\begin{aligned}\sigma _{xx}\\\sigma _{yy}\\\sigma _{xy}\end{aligned}}\right\}={\frac {K_{\rm {II}}}{\sqrt {2\pi r}}}\left\{{\begin{aligned}-\sin {\frac {\theta }{2}}(2+\cos {\frac {\theta }{2}}\cos {\frac {3\theta }{2}})\\\sin {\frac {\theta }{2}}\cos {\frac {\theta }{2}}\sin {\frac {3\theta }{2}}\\\cos {\frac {\theta }{2}}(1-\sin {\frac {\theta }{2}}\sin {\frac {3\theta }{2}})\end{aligned}}\right\}$ و $\left\{{\begin{aligned}\sigma _{rr}\\\sigma _{\theta \theta }\\\sigma _{r\theta }\end{aligned}}\right\}={\frac {K_{\rm {II}}}{\sqrt {2\pi r}}}\left\{{\begin{aligned}\sin {\frac {\theta }{2}}(1-3\sin ^{2}{\frac {\theta }{2}})\\-3\sin {\frac {\theta }{2}}\cos ^{2}{\frac {\theta }{2}}\\\cos {\frac {\theta }{2}}(1-3\sin ^{2}{\frac {\theta }{2}})\end{aligned}}\right\}$, $\sigma _{zz}=\nu _{1}(\sigma _{xx}+\sigma _{yy})=\nu _{1}(\sigma _{rr}+\sigma _{\theta \theta })$, $\sigma _{xz}=\sigma _{yz}=\sigma _{rz}=\sigma _{\theta z}=0$. $\left\{{\begin{aligned}u_{x}\\u_{y}\end{aligned}}\right\}={\frac {K_{\rm {II}}}{2E}}{\sqrt {\frac {r}{2\pi }}}\left\{{\begin{aligned}(1+\nu )\left[(2\kappa +3)\sin {\frac {\theta }{2}}+\sin {\frac {3\theta }{2}}\right]\\-(1+\nu )\left[(2\kappa -3)\cos {\frac {\theta }{2}}+\cos {\frac {3\theta }{2}}\right]\end{aligned}}\right\}$ $\left\{{\begin{aligned}u_{r}\\u_{\theta }\end{aligned}}\right\}={\frac {K_{\rm {II}}}{2E}}{\sqrt {\frac {r}{2\pi }}}\left\{{\begin{aligned}(1+\nu )\left[-(2\kappa -1)\sin {\frac {\theta }{2}}+3\sin {\frac {3\theta }{2}}\right]\\(1+\nu )\left[-(2\kappa +1)\cos {\frac {\theta }{2}}+3\cos {\frac {3\theta }{2}}\right]\end{aligned}}\right\}$ $u_{z}=-\left({\frac {\nu _{2}z}{E}}\right)(\sigma _{xx}+\sigma _{yy})=-\left({\frac {\nu _{2}z}{E}}\right)(\sigma _{rr}+\sigma _{\theta \theta })$ و در نهایت برای حالت III $\left\{{\begin{aligned}\sigma _{xz}\\\sigma _{yz}\end{aligned}}\right\}={\frac {K_{\rm {III}}}{\sqrt {2\pi r}}}\left\{{\begin{aligned}-\sin {\frac {\theta }{2}}\\\cos {\frac {\theta }{2}}\end{aligned}}\right\}$ $\left\{{\begin{aligned}\sigma _{rz}\\\sigma _{\theta z}\end{aligned}}\right\}={\frac {K_{\rm {III}}}{\sqrt {2\pi r}}}\left\{{\begin{aligned}\sin {\frac {\theta }{2}}\\\cos {\frac {\theta }{2}}\end{aligned}}\right\}$ با $\sigma _{xx}=\sigma _{yy}=\sigma _{rr}=\sigma _{\theta \theta }=\sigma _{zz}=\sigma _{xy}=\sigma _{r\theta }=0$. $u_{z}={\frac {2K_{\rm {III}}}{E}}{\sqrt {\frac {r}{2\pi }}}\left\{2(1+\nu )\sin {\frac {\theta }{2}}\right\}$, $u_{x}=u_{y}=u_{r}=u_{\theta }=0$.

رابطه با سرعت آزادسازی انرژی و J-انتگرال

در شرایط تنش صفحه‌ای، نرخ آزادسازی انرژی کرنش ($G$) برای یک ترک در حالت خالص I یا II با ضریب شدت تنش مرتبط است:

$G_{\rm {I}}=K_{\rm {I}}^{2}\left({\frac {1}{E}}\right)$

$G_{\rm {II}}=K_{\rm {II}}^{2}\left({\frac {1}{E}}\right)$

که $E$ مدول یانگ و $\nu$ نسبت پواسون ماده است. که همسانگرد، همگن و الاستیک خطی فرض می‌شود. همچنین فرض شده است که ترک در امتداد جهت ترک اولیه رشد می‌کند.

برای شرایط کرنش صفحه‌ای، رابطهٔ معادل، کمی پیچیده‌تر است:

$G_{\rm {I}}=K_{\rm {I}}^{2}\left({\frac {1-\nu ^{2}}{E}}\right)\,$

$G_{\rm {II}}=K_{\rm {II}}^{2}\left({\frac {1-\nu ^{2}}{E}}\right)\,.$

برای بارگذاری خالص حالت III،

$G_{\rm {III}}=K_{\rm {III}}^{2}\left({\frac {1}{2\mu }}\right)=K_{\rm {III}}^{2}\left({\frac {1+\nu }{E}}\right)$

که $\mu$ مدول برشی است. برای حالت کلی بارگذاری در کرنش صفحه‌ای، ترکیب خطی برقرار است:

$G=G_{\rm {I}}+G_{\rm {II}}+G_{\rm {III}}\,.$

رابطهٔ مشابهی برای تنش صفحه‌ای، با جمع کردن مقدار هر سه حالت به دست می‌آید.

روابط فوق می‌تواند برای مربوط کردن انتگرال J به ضریب شدت تنش استفاده شود. زیرا

$G=J=\int _{\Gamma }\left(W~dx_{2}-\mathbf {t} \cdot {\cfrac {\partial \mathbf {u} }{\partial x_{1}}}~ds\right)\,.$

ضریب شدت تنش بحرانی

  ضریب شدت تنش، $K$، پارامتری است که بزرگی تنش اعمال شده را بیشتر می‌کند که شامل پارامتر هندسی $Y$ (نوع بار) است. شدت تنش در هر حالت مستقیماً با بار اعمال شده به ماده متناسب است. اگر بتوان یک ترک بسیار تیز، یا یک شکاف V شکل در یک ماده ایجاد کرد، حداقل مقدار $K_{\mathrm {I} }$ را می‌توان به صورت تجربی تعیین کرد، که همان مقدار بحرانی شدت تنش مورد نیاز برای انتشار ترک است. این مقدار بحرانی که برای بارگذاری حالت I در کرنش صفحه‌ای تعیین شده، چقرمگی شکست بحرانی ($K_{\mathrm {Ic} }$) ماده نامیده می شود. واحد $K_{\mathrm {Ic} }$ تنش ضربدر ریشه طول است (مثلاً MN/m ^3/2). واحد $K_{\mathrm {Ic} }$ نشان می‌دهد که تنش شکست ماده در فاصله‌ای بحرانی باید به $K_{\mathrm {Ic} }$ برسد تا ترک منتشر شود. ضریب شدت تنش بحرانی حالت I، $K_{\mathrm {Ic} }$، متداول ترین پارامتر طراحی مهندسی در مکانیک شکست است و از این رو اگر بخواهیم مواد مقاوم به شکست را طراحی کنیم که در پل ها، ساختمان‌ها، هواپیماها یا حتی ناقوس‌ها استفاده می‌شود، باید آن را درک کنیم.

با پولیش کردن نمی‌توان ترک را تشخیص داد. به طور معمول، اگر یک ترک را بتوان دید، بسیار نزدیک به حالت تنش بحرانی است که توسط ضریب شدت تنش پیش‌بینی می‌شود.

معیار G

معیار G یک معیار شکست است که ضریب شدت تنش بحرانی (یا چقرمگی شکست) را به ضرایب شدت تنش برای سه حالت مرتبط می‌کند. این معیار شکست به صورت

$K_{\rm {c}}^{2}=K_{\rm {I}}^{2}+K_{\rm {II}}^{2}+{\frac {E'}{2\mu }}\,K_{\rm {III}}^{2}$

نوشته می‌شود که $K_{\rm {c}}$ چقرمگی شکست، $E'=E/(1-\nu ^{2})$ (برای کرنش صفحه‌ای) و $E'=E$ (برای تنش صفحه‌ای) است. ضریب شدت تنش بحرانی برای تنش صفحه‌ای اغلب به صورت $K_{\rm {c}}$ نوشته می‌شود.

مثال‌ها

صفحهٔ نامتناهی: تنش تک محوری یکنواخت

ضریب شدت تنش برای یک ترک مستقیم فرضی به طول $2a$ و عمود بر جهت بارگذاری، در یک صفحه نامتناهی، دارای میدان تنش یکنواخت $K_{\mathrm {I} }=\sigma {\sqrt {\pi a}}$ است.

ترک در یک صفحهٔ نامتناهی در حالت بارگذاری I.

ترک سکه مانند در دامنهٔ نامتناهی

ضریب شدت تنش در نوک یک ترک سکه مانند با شعاع $a$ در یک دامنه نامتناهی تحت کشش تک محوری $\sigma$برابر $K_{\rm {I}}={\frac {2}{\pi }}\sigma {\sqrt {\pi a}}\,.$ است.

ترک سکه مانند در یک دامنهٔ نامتناهی تحت کشش تک محوری.

صفحه محدود: تنش تک محوری یکنواخت

اگر ترک در مرکز در یک صفحهٔ محدود با عرض $2b$ و ارتفاع $2h$ قرار گرفته باشد، یک رابطه تقریبی برای ضریب شدت تنش $K_{\rm {I}}=\sigma {\sqrt {\pi a}}\left[{\cfrac {1-{\frac {a}{2b}}+0.326\left({\frac {a}{b}}\right)^{2}}{\sqrt {1-{\frac {a}{b}}}}}\right]\,.$ است. اگر ترک در مرکز عرض قرار نگیرد($d\neq b$)، ضریب شدت تنش در مکان A را می‌توان با بسط سری $K_{\rm {IA}}=\sigma {\sqrt {\pi a}}\left[1+\sum _{n=2}^{M}C_{n}\left({\frac {a}{b}}\right)^{n}\right]$ که در آن ضرایب $C_{n}$ را می‌توان از طریق برازش به منحنی‌های شدت تنش، برای مقادیر مختلف $d$ پیدا کرد. یک رابطهٔ مشابه (اما نه یکسان) را می‌توان برای نوک B ترک یافت. رابطه‌های جایگزین برای ضرایب شدت تنش در A و B عبارتند از $K_{\rm {IA}}=\sigma {\sqrt {\pi a}}\,\Phi _{A}\,\,,K_{\rm {IB}}=\sigma {\sqrt {\pi a}}\,\Phi _{B}$ که در آن ${\begin{aligned}\Phi _{A}&:=\left[\beta +\left({\frac {1-\beta }{4}}\right)\left(1+{\frac {1}{4{\sqrt {\sec \alpha _{A}}}}}\right)^{2}\right]{\sqrt {\sec \alpha _{A}}}\\\Phi _{B}&:=1+\left[{\frac {{\sqrt {\sec \alpha _{AB}}}-1}{1+0.21\sin \left\{8\,\tan ^{-1}\left[\left({\frac {\alpha _{A}-\alpha _{B}}{\alpha _{A}+\alpha _{B}}}\right)^{0.9}\right]\right\}}}\right]\end{aligned}}$ با $\beta :=\sin \left({\frac {\pi \alpha _{B}}{\alpha _{A}+\alpha _{B}}}\right)~,~~\alpha _{A}:={\frac {\pi a}{2d}}~,~~\alpha _{B}:={\frac {\pi a}{4b-2d}}~;~~\alpha _{AB}:={\frac {4}{7}}\,\alpha _{A}+{\frac {3}{7}}\,\alpha _{B}\,.$ در عبارات فوق $d$، فاصلهٔ مرکز ترک تا نزدیکترین مرز به نقطه A است. توجه داشته باشید که وقتی $d=b$ عبارات بالا به عبارت تقریبی برای یک ترک مرکزی ساده نمی‌شوند.

ترک در یک صفحهٔ محدود در حالت بارگذاری I.

ترک روی لبه در صفحه تحت تنش تک محوری

برای یک صفحه دارای ابعاد $2h\times b$ دارای یک ترک لبه‌ای به طول $a$، در صورتی که ابعاد صفحه به گونه ای باشد که $h/b\geq 0.5$ و $a/b\leq 0.6$ ضریب شدت تنش در نوک ترک تحت تنش تک محوری $\sigma$ است $K_{\rm {I}}=\sigma {\sqrt {\pi a}}\left[1.122-0.231\left({\frac {a}{b}}\right)+10.55\left({\frac {a}{b}}\right)^{2}-21.71\left({\frac {a}{b}}\right)^{3}+30.382\left({\frac {a}{b}}\right)^{4}\right]\,.$ برای هنگامی که $h/b\geq 1$ و $a/b\geq 0.3$، ضریب شدت تنش را می‌توان توسط رابطه $K_{\rm {I}}=\sigma {\sqrt {\pi a}}\left[{\frac {1+3{\frac {a}{b}}}{2{\sqrt {\pi {\frac {a}{b}}}}\left(1-{\frac {a}{b}}\right)^{3/2}}}\right]\,$ تقریب زد.

ترک روی لبه در صفحهٔ محدود تحت تنش تک محوری

صفحهٔ نامتناهی: ترک مورب در میدان تنش دو محوری

برای یک ترک مورب به طول $2a$ در یک میدان تنش دو محوره با تنش $\sigma$ در جهت $y$ و $\alpha \sigma$ در جهت $x$، ضرایب شدت تنش ${\begin{aligned}K_{\rm {I}}&=\sigma {\sqrt {\pi a}}\left(\cos ^{2}\beta +\alpha \sin ^{2}\beta \right)\\K_{\rm {II}}&=\sigma {\sqrt {\pi a}}\left(1-\alpha \right)\sin \beta \cos \beta \end{aligned}}$ هستند به طوری که $\beta$، زاویه ایجاد شده توسط ترک با محور $x$ است.

یک ترک اریب در یک صفحه نازک تحت بارگذاری دو محوره.

ترک در یک صفحه تحت نیروی نقطه‌ای در صفحه

یک صفحه با ابعاد $2h\times 2b$ حاوی یک ترک به طول $2a$ را در نظر بگیرید. یک نیروی نقطه‌ای با مؤلفه‌های $F_{x}$ و $F_{y}$ در نقطه ( $x,y$ ) در صفحه اعمال می‌شود. برای شرایطی که صفحه در مقایسه با اندازه ترک بزرگ است و محل نیرو نسبتاً نزدیک به ترک است، یعنی $h\gg a$ ، $b\gg a$ ، $x\ll b$ ، $y\ll h$ ، صفحه را می توان نا‌متناهی در نظر گرفت. در آن صورت، برای ضریب شدت تنش حاصل از $F_{x}$ در نوک ترک B ( $x=a$) ${\begin{aligned}K_{\rm {I}}&={\frac {F_{x}}{2{\sqrt {\pi a}}}}\left({\frac {\kappa -1}{\kappa +1}}\right)\left[G_{1}+{\frac {1}{\kappa -1}}H_{1}\right]\\K_{\rm {II}}&={\frac {F_{x}}{2{\sqrt {\pi a}}}}\left[G_{2}+{\frac {1}{\kappa +1}}H_{2}\right]\end{aligned}}$ هستند. به طوری که ${\begin{aligned}G_{1}&=1-{\text{Re}}\left[{\frac {a+z}{\sqrt {z^{2}-a^{2}}}}\right]\,,\,\,G_{2}=-{\text{Im}}\left[{\frac {a+z}{\sqrt {z^{2}-a^{2}}}}\right]\\H_{1}&={\text{Re}}\left[{\frac {a({\bar {z}}-z)}{({\bar {z}}-a){\sqrt {{\bar {z}}^{2}-a^{2}}}}}\right]\,,\,\,H_{2}=-{\text{Im}}\left[{\frac {a({\bar {z}}-z)}{({\bar {z}}-a){\sqrt {{\bar {z}}^{2}-a^{2}}}}}\right]\end{aligned}}$ با $z=x+iy$ ، ${\bar {z}}=x-iy$ ، $\kappa =3-4\nu$ برای کرنش صفحه‌ای، $\kappa =(3-\nu )/(1+\nu )$ برای تنش صفحه‌ای، و $\nu$ نسبت پواسون. ضرایب شدت تنش برای $F_{y}$ در نوک B ${\begin{aligned}K_{\rm {I}}&={\frac {F_{y}}{2{\sqrt {\pi a}}}}\left[G_{2}-{\frac {1}{\kappa +1}}H_{2}\right]\\K_{\rm {II}}&=-{\frac {F_{y}}{2{\sqrt {\pi a}}}}\left({\frac {\kappa -1}{\kappa +1}}\right)\left[G_{1}-{\frac {1}{\kappa -1}}H_{1}\right]\,.\end{aligned}}$ هستند. ضرایب شدت تنش در نوک A ($x=-a$) را می توان از روابط فوق تعیین کرد. برای بار $F_{x}$ در محل $(x,y)$، $K_{\rm {I}}(-a;x,y)=-K_{\rm {I}}(a;-x,y)\,,\,\,K_{\rm {II}}(-a;x,y)=K_{\rm {II}}(a;-x,y)\,.$ به طور مشابه برای بار $F_{y}$، $K_{\rm {I}}(-a;x,y)=K_{\rm {I}}(a;-x,y)\,,\,\,K_{\rm {II}}(-a;x,y)=-K_{\rm {II}}(a;-x,y)\,.$

یک ترک در یک صفحه تحت اثر یک نیروی موضعی با اجزاء $F_{x}$ و $F_{y}$ .

ترک بارگذاری شده در صفحه

اگر ترک توسط نیروی نقطه‌ای $F_{y}$ واقع شده در $y=0$ و $-a<x<a$ بارگذاری شود، ضرایب شدت تنش در نقطه B عبارتند از $K_{\rm {I}}={\frac {F_{y}}{2{\sqrt {\pi a}}}}{\sqrt {\frac {a+x}{a-x}}}\,,\,\,K_{\rm {II}}=-{\frac {F_{x}}{2{\sqrt {\pi a}}}}\left({\frac {\kappa -1}{\kappa +1}}\right)\,.$ اگر نیرو به طور یکنواخت بین $-a<x<a$ توزیع شده باشد، سپس ضریب شدت تنش در نوک B برابر است با $K_{\rm {I}}={\frac {1}{2{\sqrt {\pi a}}}}\int _{-a}^{a}F_{y}(x)\,{\sqrt {\frac {a+x}{a-x}}}\,{\rm {d}}x\,,\,\,K_{\rm {II}}=-{\frac {1}{2{\sqrt {\pi a}}}}\left({\frac {\kappa -1}{\kappa +1}}\right)\int _{-a}^{a}F_{y}(x)\,{\rm {d}}x,\,.$

یک ترک بارگذاری شده در صفحه.

نمونه کششی فشرده

ضریب شدت تنش در نوک ترک یک نمونه کششی فشرده ${\begin{aligned}K_{\rm {I}}&={\frac {P}{B}}{\sqrt {\frac {\pi }{W}}}\left[16.7\left({\frac {a}{W}}\right)^{1/2}-104.7\left({\frac {a}{W}}\right)^{3/2}+369.9\left({\frac {a}{W}}\right)^{5/2}\right.\\&\qquad \left.-573.8\left({\frac {a}{W}}\right)^{7/2}+360.5\left({\frac {a}{W}}\right)^{9/2}\right]\end{aligned}}$ است که $P$ بار اعمال شده، $B$ ضخامت نمونه، $a$ طول ترک و $W$ عرض نمونه است.

نمونه کششی فشرده برای تست چقرمگی شکست.

نمونه خمشی شکاف تک لبه

ضریب شدت تنش در نوک ترک یک نمونه خمشی شکاف تک لبه ${\begin{aligned}K_{\rm {I}}&={\frac {4P}{B}}{\sqrt {\frac {\pi }{W}}}\left[1.6\left({\frac {a}{W}}\right)^{1/2}-2.6\left({\frac {a}{W}}\right)^{3/2}+12.3\left({\frac {a}{W}}\right)^{5/2}\right.\\&\qquad \left.-21.2\left({\frac {a}{W}}\right)^{7/2}+21.8\left({\frac {a}{W}}\right)^{9/2}\right]\end{aligned}}$ که $P$ بار اعمال شده، $B$ ضخامت نمونه، $a$ طول ترک و $W$ عرض نمونه است.

نمونه خمشی تک لبه (که نمونه خمشی سه نقطه نیز نامیده می شود) برای تست چقرمگی شکست.

جستارهای وابسته

• مکانیک شکست
• چقرمگی شکست
• نرخ آزاد شدن انرژی کرنش
• J-انتگرال
• تئوری شکست مواد
• قانون پاریس