سمت‌گشت

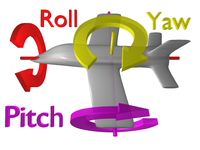
سَمت‌گَشت^[۱] (انگلیسی: Yaw) به چرخش یک جسم حول محور عمودی آن اشاره دارد. این محور عمودی معمولاً به عنوان محور z شناخته می‌شود. برای تجسم این حرکت، یک هواپیما را تصور کنید که دماغه‌اش را به چپ یا راست می‌چرخاند، در حالی که ارتفاع و شیب آن ثابت می‌ماند. در این مثال، هواپیما در حال انجام حرکت سمت‌گشت است.

به تعریف دیگر، چرخش سمتی یا سمت‌گشت، یک حرکت حول محور سمت‌گشت یک جسم صلب است که جهت اشاره آن را به چپ یا راست جهت حرکت آن تغییر می‌دهد. آهنگ سمت‌گشت^[۲] یا سرعت سمت‌گشت یک خودرو، هواپیما، پرتابه یا جسم صلب دیگر، سرعت زاویه‌ای این چرخش یا نرخ تغییر زاویه عنوان زمانی است که هواپیما افقی است. معمولاً بر حسب درجه بر ثانیه یا رادیان بر ثانیه اندازه‌گیری می‌شود.

مفهوم مهم دیگر گشتاور سمت‌گشت است که مؤلفه گشتاور نیرو حول محور سمت‌گشت است.

اندازه‌گیری

سرعت سمت‌گشت را می‌توان با اندازه‌گیری سرعت زمین در دو نقطه هندسی جدا شده روی بدنه، یا با ژیروسکوپ اندازه‌گیری کرد، یا می‌توان آن را از شتاب‌سنج و موارد مشابه ترکیب کرد. این معیار اصلی نحوه درک بصری رانندگان از چرخش خودرو است.

در کنترل پایداری الکترونیکی وسایل نقلیه مهم است. آهنگ سمت‌گشت مستقیماً با شتاب جانبی وسیله نقلیه که با سرعت ثابت در اطراف یک شعاع ثابت می‌چرخد، با رابطه زیر مرتبط است:

سرعت مماسی * سرعت سمت‌گشت = شتاب جانبی = سرعت مماسی ^ ۲ / شعاع چرخش، در واحدهای مناسب

قرارداد علامت را می‌توان با توجه دقیق به دستگاه‌های مختصات ایجاد کرد.

در یک مانور کلی‌تر که شعاع تغییر می‌کند و/یا سرعت تغییر می‌کند، رابطه فوق دیگر برقرار نیست.

کنترل آهنگ سمت‌گشت

آهنگ سمت‌گشت را می‌توان با شتاب‌سنج‌ها در محور عمودی اندازه‌گیری کرد. هر وسیله‌ای که برای اندازه‌گیری آهنگ سمت‌گشت در نظر گرفته شده است، حسگر آهنگ سمت‌گشت نامیده می‌شود.

وسایل نقلیه جاده‌ای

مطالعه پایداری یک وسیله نقلیه جاده‌ای نیازمند تقریب معقولی برای معادلات حرکت است.

نمودار یک وسیله نقلیه چهار چرخ را نشان می‌دهد که در آن محور جلو a متر جلوتر از مرکز جرم و محور عقب b متر به سمت عقب از مرکز ثقل قرار دارد. بدنه خودرو در جهت $\theta$ (theta) است در حالی که در جهت $\psi$ (psi) حرکت می‌کند. به‌طورکلی، این‌ها یکسان نیستند. آج لاستیک‌ها در ناحیه نقطه تماس در جهت حرکت است، اما توپی‌ها با بدنه خودرو تراز می‌شوند و فرمان در مرکز نگه داشته می‌شود. لاستیک‌ها با چرخش برای تطبیق با این ناهماهنگی، منحرف می‌شوند و در نتیجه نیروهای جانبی ایجاد می‌کنند.

از مطالعه پایداری جهتی، با نشان دادن سرعت زاویه‌ای $\omega$ ، معادلات حرکت عبارتند از:

{\frac {d\omega }{dt}}=2k{\frac {(a-b)}{I}}\beta -2k{\frac {(a^{2}+b^{2})}{VI}}\omega

{\frac {d\beta }{dt}}=-{\frac {4k}{MV}}\beta +(1-2k){\frac {(b-a)}{MV^{2}}}\omega

با $M$ جرم وسیله نقلیه، $V$ سرعت وسیله نقلیه و $\beta =\theta -\psi$ زاویه کلی وسیله نقلیه.

ضریب ${\frac {d\beta }{dt}}$ را با تشبیه به یک دمپر جرم-فنر که معادله حرکت مشابهی دارد، 'میرایی' می‌نامیم. با همین قیاس، ضریب $\beta$ را 'سختی' می‌نامیم، زیرا عملکرد آن بازگرداندن سیستم به انحراف صفر است، به همان شیوه یک فنر.

شکل راه‌حل فقط به علائم عبارات میرایی و سختی بستگی دارد. چهار نوع راه‌حل ممکن در شکل ارائه شده است.

تنها راه حل رضایت بخش مستلزم مثبت بودن هم سختی و هم میرایی است. اگر مرکز ثقل جلوتر از مرکز فاصله بین محورها $(b>a)$ باشد، این همیشه مثبت خواهد بود و وسیله نقلیه در همه سرعت‌ها پایدار خواهد بود. با این حال، اگر دورتر عقب باشد، این عبارت پتانسیل منفی شدن در بالای سرعت داده شده توسط:

V^{2}={\frac {2k(a+b)^{2}}{M(a-b)}}

بالاتر از این سرعت، وسیله نقلیه از نظر جهتی (سمت‌گشت) ناپایدار خواهد بود. اصلاحات برای اثر نسبی لاستیک‌های جلو و عقب و نیروهای فرمان در مقاله اصلی موجود است.

رابطه با سایر سیستم‌های چرخشی

این چرخش‌ها چرخش‌های ذاتی هستند و حساب پشت آن‌ها شبیه به فرمول‌های فرنت-سرت است. انجام چرخش در یک چارچوب مرجع ذاتی معادل ضرب راست ماتریس مشخصه آن (ماتریسی که بردار قاب مرجع را به عنوان ستون دارد) در ماتریس چرخش است.

تاریخچه

اولین هواپیمایی که کنترل فعال در هر سه محور را نشان داد، گلایدر برادران رایت در سال ۱۹۰۲ بود.^[۳]

جستارهای وابسته

منابع

↑ Toolforge.org. “جستجوی واژه‌های مصوب فرهنگستان زبان و ادب فارسی، ” 2024. https://farhangestan.toolforge.org/results?word=yaw&wordstart=&wordend=&hozeh=&daftar=همهٔ+دفترها.
↑ Toolforge.org. “جستجوی واژه‌های مصوب فرهنگستان زبان و ادب فارسی، ” 2024. https://farhangestan.toolforge.org/results?word=yaw&wordstart=&wordend=&hozeh=&daftar=همهٔ+دفترها.
↑ [[۱](https://www.grc.nasa.gov/WWW/K-12/airplane/rotations.html) "Aircraft rotations"]. مرکز تحقیقات گلن. 2015-05-05. Retrieved 2018-10-13. {{cite web}}: Check |url= value (help)

مشارکت‌کنندگان ویکی‌پدیا. «Yaw (rotation)». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۳ اوت ۲۰۲۴.

[1] Toolforge.org. “جستجوی واژه‌های مصوب فرهنگستان زبان و ادب فارسی، ” 2024. https://farhangestan.toolforge.org/results?word=yaw&wordstart=&wordend=&hozeh=&daftar=همهٔ+دفترها.

[2] Toolforge.org. “جستجوی واژه‌های مصوب فرهنگستان زبان و ادب فارسی، ” 2024. https://farhangestan.toolforge.org/results?word=yaw&wordstart=&wordend=&hozeh=&daftar=همهٔ+دفترها.

[3] [[۱](https://www.grc.nasa.gov/WWW/K-12/airplane/rotations.html) "Aircraft rotations"]. مرکز تحقیقات گلن. 2015-05-05. Retrieved 2018-10-13. {{cite web}}: Check |url= value (help)

[۱]

[۲]

[۳]