سطح مقطع پراکندگی

مساحت فرضی ای که احتمال پراکنده شدن نور یا تابش‌های دیگر را به وسیله ذرات در مرکز پراکندگی شرح می‌دهد، سطح مقطع پراکندگی می‌گویند؛ که اندازه‌گیریی از برهم کنش بین ذره پراکنده شده و یک یا چند مرکز پراکندگی است.

تعریف

پراکندگی یک ذره از یک مرکز پراکندگی یگانه ساده‌ترین نوع تعریف سطح مقطع دیفرانسیلی پراکندگی ست:

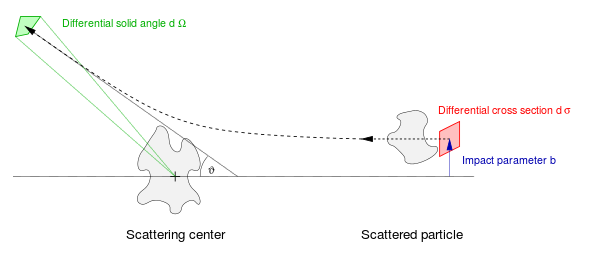
پارامتر برخورد فاصله عمودی از خط سیر ذره ورودی است. سطح مقطع دیفرانسیلی المان مساحت در صفحه پارامتر برخورد است $d\sigma =d^{2}b$ ، که در آن b پارامتر برخورد است. سطح مقطع دیفرانسیلی حاصل تقسیم المان دیفرانسیلی مساحت بر المان دیفرانسیلی زاویه فضایی در جهت مسیر خروجی ذرات است: $\left|{\frac {d\sigma }{d\Omega }}\right|$

این کسر تغییرات در پارامتر برخورد که لازمه تغییرات در جهت مسیر خروجی است را شرح می‌دهد. تعریف کمی با این موضوع که متغیر مستقل (مخرج کسر) متغیر وابسته به شرایط اولیه (صورت کسر) را شرح می‌دهد متضاد است. سطح مقطع دیفرانسیلی همیشه باید مثبت باشد، حتی در موارد با فرکانس بالا در برهم کنش‌ها دفعی ناحیه محدود، پارامتر برخورد بزرگ انحرافهای کوچکی را موجب می‌شوند. در مسائل با تقارن چرخشی، زاویه سمتی $\varphi$ در فرایند پراکندگی تغییر نمی‌کند و سطح مقطع دیفرانسیلی تبدیل می‌شود به:

{\frac {b}{\sin \vartheta }}\;\left|{\frac {db}{d\vartheta }}\right|\ ,

همان‌طور که در شکل نشان داده شده‌است $\vartheta$ زاویه بین جهت پرتو ورودی و خروجی است.

سطح مقطع کل انتگرال سطح مقطع دیفرانسیلی روی همه زاویه فضایی است.

\sigma _{\text{tot}}=\oint d\Omega \;{\frac {d\sigma }{d\Omega }}

سطح مقطع کل اندازه مشخص معنی داری از برهم کنش بین ذره پراکنده شده و مرکز پراکندگی فراهم می‌کند.

وقتی فقط برخورد بین پرتو و نمونه در نظر گرفته شود، یک اتم از نمونه معمولاً به عنوان مرکز پراکندگی شناخته می‌شود. در آزمایش‌های شتابدهنده‌ها هر دو ذره برخورد کننده شتاب داده شده‌اند، پس هر دو ذره می‌توانند ذره پراکنده شده یا مرکز پراگندگی باشند. وقتی یک ذره به وسیله یک قسمت گسترده پراکنده می‌شود، مرکز پراکندگی چند گانه در نظر گرفته می‌شود.

مثال: برخورد الاستیک دو کره سخت

برخورد الاستیک دو کره سخت یک مثال آموزنده است که درک درستی از نامیدن کمیت سطح مقطع به ما می‌دهد. $R$ و $r$ به ترتیب شعاع‌های مرکز پراکندگی و کره پراکنده شده هستند، $b$ پارامتر برخورد و $\vartheta$ همان‌طور که در بالا گفته شد زاویه قطبی مسیر خروجی است. پس سطح مقطع دیفرانسیلی خواهد شد

\left|{\frac {d\sigma }{d\Omega }}\right|={\frac {1}{4}}(r+R)^{2}

و سطح مقطع کل چنین است

\sigma _{\text{tot}}=\pi \;(r+R)^{2}\ .

پس در این مورد سطح مقطع کل پراکندگی متناسب با مساحت دایره‌ای با شعاع ( $r+R$ ) است که در آن مر کز جرم کره ورودی منحرف شده، و پس از آن با یک مرکز پراکندگی ثابت به راه خود ادامه می‌دهد.

فیزیک پراکندگی با مرکز پراکندگی یگانه

مکانیک کلاسیک

در مکانیک کلاسیک، سطح مقطع دیفرانسیلی به صورت زیر تعریف می‌شود: شدت پرتو ورودی به یک مرکز پراکندگی $I_{0}$ (تعداد ذرات اندازه‌گیری شده در واحد مساحت در واحد زمان) است. عموماً، زاویه‌ای که از آن یک ذره پراکنده می‌شود تابعی از پارامتر برخورد است. تعداد ذرات پراکنده شده در واحد زاویه فضایی در واحد زمان شدت تابش $I_{\text{s}}$ نامیده می‌شود. سطح مقطع دیفرانسیلی تعریف می‌شود

{d\sigma  \over d\Omega }={\frac {I_{\text{s}}}{I_{0}}}.

دقت کنید واحد این کمیت مساحت است. بنابراین فقط به شکل هندسی مر کز پراکندگی وابسته است، و به تابش ورودی یا فاصله آشکار ساز از مرکز پراکندگی وابسته نیست. تفسیر هندسی آن: ذراتی را در نظر بگیرید که در یک زاویه فضایی $d\Omega$ پراکنده می‌شود و سؤال اینجاست پارامتر برخورد چه مقدار از آنها را تولید می‌کند. این پارامترهای برخورد از یک مساحت دیفرانسیلی در فضا $d\sigma$ نامیده می‌شود. پس سطح مقطع دیفرانسیلی خواهد شد: ${d\sigma \over d\Omega }.$

مکانیک کوانتومی

در مکانیک کوانتومی، تابع موج ذرات ورودی یک موج تخت با دامنه $e^{ikz}$ است. به‌طور کلی موج پراکنده شده به فرم: $f(\theta ,\phi ){\frac {e^{ikr}}{r}}.$ خواهد شد.

سطح مقطع دیفرانسیلی طبق تعریف خواهد شد

{d\sigma  \over d\Omega }=|f|^{2}.

که تفسیر ساده‌ای از احتمال پیدا کردن ذرات پراکنده شده در یک زاویه فضایی را می‌دهد. انتگرال سطح مقطع انتگرال سطح مقطع دیفرانسیلی روی همه فضا است (۴π steradian):

\sigma =\int {d\sigma  \over d\Omega }\,d\Omega .

سطح مقطع بنابراین اندازه مؤثر مساحتی است که بوسیله ذرات تماسی دیده می‌شود و با واحد مساحت نشان داده می‌شود. واحد مورد استفاده معمولاً cm² است، بارن (1b=10⁻²⁸ m²) و شد(1shed=10⁻²⁴ b)واحدهای مناسب تری برای سطح مقطع هستند. سطح مقطع دو ذره (وقتی که دو ذره با هم برخورد کنند) اندازه برهم‌کنش بین دو ذره است. سطح مقطع متناسب با احتمال وقوع برخورد است؛ برای مثال در یک آزمایش پراکندگی تعداد ذراتی که در واحد زمان پراکنده شده‌اند (جربان ذرات پراکنده شده I_r) فقط به تعداد ذرات ورودی در واحد زمان بستگی دارد (جریان ذرات ورودی I_i). نوع برهمکنش و تعداد ذرات در واحد سطح N مشخصات نمونه هستند. برای $N\sigma \ll 1$ داریم:

$I_{\text{r}}=I_{\text{i}}N\sigma \,$

$\sigma ={{I{\text{r}}} \over {I_{\text{i}}}}{{1} \over {N}}$

که‌درآن ${I_{\text{r}}} \over {I_{\text{i}}}$ احتمال برهم کنش است.

ارتباط با ماتریس S

اگر جرم کاهش یافته و اندازه حرکت سیستم برخورد m_i، p_i و m_f، p_f به ترتیب قبل و بعد از برخورد باشند، سطح مقطع دیفرانسیلی خواهد شد:

${d\sigma \over d\Omega }=(2\pi )^{4}m_{i}m_{f}{p_{f} \over p_{i}}|T_{fi}|^{2},$

و جایی که روی سطح باشد ماتریس T به این صورت تعریف می‌شود:

$S_{fi}=\delta _{fi}-2\pi i\delta (E_{f}-E_{i})\delta (\mathbf {p} _{i}-\mathbf {p} _{f})T_{fi}$

در عبارت ماتریس پراکندگی S, $\delta$ تابع دلتای دیراک است. محاسبه ماتریس S هدف اصلی تئوری پراکندگی است.

فیزیک ذرات

سطح مقطع دیفرانسیلی و سطح مقطع کل مهم‌ترین کمیتهای قابل اندازه‌گیری در فیزیک ذرات هستند. به جای زاویه فضایی، تکانه انتقالی اغلب به عنوان متغیر مستقل از سطح مقطع دیفرانسیلی انتخاب می‌شود. سطح مقطع‌های دیفرانسیلی در پراکندگی غیر الاستیک شامل پیک‌هایی است که تعیین کننده ذرات با انرژی و طول عمر مشخص هستند. به عنوان نتیجه، سطح مقطع کلی از هدرن‌ها (ذرات با برهم‌کنش قوی) بک فاکتور ۳ از تقارن رنگی کوارک‌ها می‌گیرد، و دانشمندان این تقارن را کشف می‌کنند.

پراکندگی نور روی سطوح گسترده

در زمینه پراکندگی نور روی سطوح گسترده، سطح مقطع پراکندگی σ_scat احتمال این است که نور به وسیله ذرات میکروسکوپی پراکنده شود. عموماً سطح مقطع پراکندگی با سطح مقطع هندسی یک ذره تفاوت دارد چراکه سطح مقطع پراکندگی علاوه بر طول موج و ثابت دی‌الکتریک، به شکل و اندازه ذره نیز بستگی دارد. سطح مقطع کل σ، مجموع سطح مقطع‌های جذب و پراکندگی و تابش است.

$\sigma =\sigma _{\text{A}}+\sigma _{\text{S}}+\sigma _{\text{L}}.\$

سطح مقطع کل به شدت نور جذب شده بر طبق قانون لامبرت، که بیان می‌کند جذب متناسب با غلظت است، بستگی دارد: $A_{\lambda }=Cl\sigma$ که A_λ جذب در طول موج داده شده‌است، C غلظت و l طول مسیر است. فرایند جذب نور لگاریتمی است:^[۱]

$A_{\lambda }=-\log {\mathcal {T}}.\$

ارتباط با اندازه فیزیکی

ارتباط ساده‌ای بین سطح مقطع پراکندگی و اندازه فیزیکی ذرات وجود ندارد چنان‌که سطح مقطع پراکندگی بستگی به طول موج تابش دارد. این موضوع در هنگام رانندگی در هوای مه‌آلود دیده می‌شود: قطرات ریز آب نور قرمز را کمتراز طول موج‌های کوتاه‌تر پراکنده می‌کنند. نور قرمز وسایل نقلیه واضح‌تر از نور سفید آنهاست. پس سطح مقطع پراکندگی قطرات آب برای نور قرمز، از طول موج‌های کوتاه‌تر کوچک‌ترند. هرچند ذرات اندازه فیزیکی یکسانی دارند.

گستره هواسنجی

سطح مقطع پراکندگی به گستره هواسنجی ارتباط دارد، L_V:

$L_{\text{V}}={\frac {3.9}{C\sigma _{\text{scat}}}}.\$

کمیت C σ_scat در بعضی مواقع b_scat را نشان می‌دهد (ضریب پراکندگی در واحد طول).^[۲]

منابع

↑ Bajpai, P.K. "2. Spectrophotometry". Biological Instrumentation and Biology. ISBN 81-219-2633-5.
↑ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "Scattering cross-section, σ_scat".

مشارکت‌کنندگان ویکی‌پدیا. «Scattering_cross-section». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۱۴ می ۲۰۱۴.

Wikipedia contributors, "Scattering cross section," Wikipedia, The Free Encyclopedia

جستارهای وابسته

پراکندگی

[1] Bajpai, P.K. "2. Spectrophotometry". Biological Instrumentation and Biology. ISBN 81-219-2633-5.

[2] IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "Scattering cross-section, σ_scat".

[۱]

[۲]