روش شیب افت

روش شیب افت یکی از روش‌های تحلیل سازه‌ها برای تحلیل تیرها و قاب ها می‌باشد که در سال ۱۹۱۵ توسط جورج منی ابداع شده‌است. تا قبل از معرفی روش توزیع لنگر، روش شیب افت به مدت یک دهه به صورت گسترده ای برای تحلیل سازه ها مورد استفاده قرار می‌گرفت.

آشنایی

در روش شیب افت با جایگزینی معادلات شیب افت در معادلات تعادل، میزان دوران در گره‌های سازه به دست می آید و سپس با جایگزینی دوران‌های به دست آمده در معادلات شیب افت، مقدار لنگر در انتهای عضوهای سازه تعیین می‌شود.

معادلات شیب افت

معادلات شیب افت مقدار لنگر در انتهای اعضای سازه را بر حسب دوران گره‌های سازه بیان می‌کنند. معادلات شیب افت برای عضو ab به طول $L_{ab}$ و سختی خمشی $E_{ab}I_{ab}$ به صورت زیر نوشته می‌شوند:

$M_{ab}=2{\frac {E_{ab}I_{ab}}{L_{ab}}}\left(2\theta _{a}+\theta _{b}-3{\frac {\Delta }{L_{ab}}}\right)$

$M_{ba}=2{\frac {E_{ab}I_{ab}}{L_{ab}}}\left(\theta _{a}+2\theta _{b}-3{\frac {\Delta }{L_{ab}}}\right)$

در این معادلات $\theta _{a}$, $\theta _{b}$ به ترتیب نشان دهنده شیب در انتهای a و b عضو (دوران گره‌های a و b) هستند و $\Delta$ میزان تغییر مکان نسبی بین دو انتهای a و b عضو می‌باشد . عدم وجود سطح مقطع عضو در این معادلات بیانگر آنست که روش شیب افت از اثر تغییرشکل‌های محوری و برشی چشم پوشی می‌کند. معادلات شیب افت همچنین می‌توانند با استفاده از ضریب سختی $K={\frac {I_{ab}}{L_{ab}}}$ و زاویه دوران عضو $\psi ={\frac {\Delta }{L_{ab}}}$ به این شکل نوشته شوند:

$M_{ab}=2E_{ab}K\left(2\theta _{a}+\theta _{b}-3\psi \right)$

$M_{ba}=2E_{ab}K\left(\theta _{a}+2\theta _{b}-3\psi \right)$

به دست آوردن معادلات شیب افت

هنگامی که لنگرهای متمرکز $M_{ab}$ و $M_{ba}$ در جهت عقربه‌های ساعت در دو انتهای یک تیر به طول $L_{ab}$ و سختی خمشی $E_{ab}I_{ab}$ وارد می‌شوند، دوران دو انتهای تیر نیز در همان جهت عقربه‌های ساعت خواهد بود. مقدار این دوران‌ها با استفاده از روش کار مجازی به صورت زیر محاسبه می‌شود:

$\theta _{a}-{\frac {\Delta }{L_{ab}}}={\frac {L_{ab}}{3E_{ab}I_{ab}}}M_{ab}-{\frac {L_{ab}}{6E_{ab}I_{ab}}}M_{ba}$

$\theta _{b}-{\frac {\Delta }{L_{ab}}}=-{\frac {L_{ab}}{6E_{ab}I_{ab}}}M_{ab}+{\frac {L_{ab}}{3E_{ab}I_{ab}}}M_{ba}$

با مرتب کردن این دو معادله، معادلات شیب افت به دست می آیند.

شرایط تعادل

تعادل در گره ها

شرایط تعادل گره‌ها ایجاب می‌کند که لنگرهای وارد به هر گره با یک درجه آزادی باید در تعادل باشند. بنابراین:

$\Sigma \left(M^{f}+M_{member}\right)=\Sigma M_{joint}$

در معادله بالا $M_{member}$ لنگرهای انتهای عضو، $M^{f}$ لنگرهای گیرداری و $M_{joint}$ لنگرهای خارجی وارد بر عضو هستند.

تعادل برش

وقتی کل عضو به عنوان یک جسم صلب دوران دارد (تغییرمکان نسبی دو انتهای عضو مخالف صفر است)، علاوه بر معادلات تعادل لنگر، تعادل برش نیز باید نوشته شود تا تعداد معادلات و مجهولات با هم برابر گردد.

مراحل گام به گام

تحلیل سازه‌ها به روش شیب افت شامل مراحل گام به گام زیر است:

۱- مجهول‌های مسئله را تعیین کنید. دوران در تمام گره‌ها (به غیر از گره‌های گیردار) مجهول هستند. همچنین تغییر مکان نسبی دو سر اعضا نیز مجهول محسوب می‌شوند.

۲- نمودار آزاد تمام اعضا و گره‌ها را رسم کنید و لنگر، برش و نیروی محوری را در انتهای اعضا و روی گره‌ها نشان دهید. قرار داد علامت را فراموش نکنید. لنگر و دوران ساعتگرد در انتهای اعضا مثبت محسوب می‌شود.

۳- به ازای هر مجهول یک معادله تعادل بنویسید. برای مجهولات دوران باید تعادل لنگر در گره مربوطه را بنویسید. برای مجهولات تغییر مکان باید معادله تعادل برش را در همان جهت تغییرمکان برای نمودار آزاد عضو متناظر و گره‌های متصل به آن بنویسید و سپس با استفاده از نمودار آزاد عضو، برش‌ها را در معادله به صورت مجموع لنگر دو انتهای عضو تقسیم بر طول عضو بنویسید.

۴- معادلات شیب افت را برای لنگرهای انتهای اعضا بنویسید و آن‌ها را در معادلات تعادل که در گام ۳ به دست آورده اید جایگزین نمایید.

۵- با حل سیستم معادلات به دست آمده، مقدار مجهولاتی را که در گام ۱ تعیین کرده اید به دست آورید. توجه کنید که جواب‌های مثبت نشان دهنده دوران ساعتگرد و جواب‌های منفی نشان دهنده دوران‌های پاد ساعتگرد هستند.

۶- مقادیر به دست آمده برای مجهولات را در معادلات شیب افت که در مرحلۀ ۴ نوشته اید جایگزین کنید تا مقادیر لنگرهای انتهای اعضا را به دست آورید.

۷- با استفاده از نمودارهای آزاد که در مرحله ۲ رسم کرده اید، مقادیر برش و نیروی محوری در انتهای اعضا و همچنین عکس‌العمل‌های سازه را تعیین کنید.

مثال

مثال

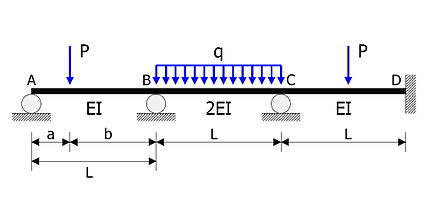
می خواهیم تیر نشان داده شده در شکل را که دارای مشخصات زیر است تحلیل کنیم. اعضای CD، BC ،AB دارای طول یکسان برابر با $L=10\ m$ هستند. سختی خمشی اعضا به ترتیب برابر با EI و EI، 2EI است. بار متمرکز $P=10\ kN$ در فاصله $a=3\ m$ از تکیه گاه A وارد می‌شود. بار گسترده $q=1\ kN/m$ روی دهانه BC وارد می‌شود. بار متمرکز $P=10\ kN$ در وسط دهانه CD وارد می‌گردد. طبق قرارداد لنگرها و دوران‌های ساعتگرد را با علامت مثبت در نظر می‌گیریم.

درجات آزادی

دوران‌های $\theta _{A}$, $\theta _{B}$, $\theta _{C}$ در گره‌های C، B، A مجهول‌های مسئله هستند. دوران گره D به دلیل گیرداری برابر با صفر است. تغییر مکان نسبی بین گره‌ها نیز در این مسئله صفر است.

لنگرهای گیرداری

لنگرهای گیرداری در این مسئله در زیر محاسبه شده اند:

$M_{AB}^{f}=-{\frac {Pab^{2}}{L^{2}}}=-{\frac {10\times 3\times 7^{2}}{10^{2}}}=-14.7\mathrm {\,kN\,m}$

$M_{BA}^{f}={\frac {Pa^{2}b}{L^{2}}}={\frac {10\times 3^{2}\times 7}{10^{2}}}=6.3\mathrm {\,kN\,m}$

$M_{BC}^{f}=-{\frac {qL^{2}}{12}}=-{\frac {1\times 10^{2}}{12}}=-8.333\mathrm {\,kN\,m}$

$M_{CB}^{f}={\frac {qL^{2}}{12}}={\frac {1\times 10^{2}}{12}}=8.333\mathrm {\,kN\,m}$

$M_{CD}^{f}=-{\frac {PL}{8}}=-{\frac {10\times 10}{8}}=-12.5\mathrm {\,kN\,m}$

$M_{DC}^{f}={\frac {PL}{8}}={\frac {10\times 10}{8}}=12.5\mathrm {\,kN\,m}$

معادلات شیب افت

معادلات شیب افت برای این مسئله به صورت زیر نوشته می‌شوند:

$M_{AB}={\frac {EI}{L}}\left(4\theta _{A}+2\theta _{B}\right)=0.4EI\theta _{A}+0.2EI\theta _{B}$

$M_{BA}={\frac {EI}{L}}\left(2\theta _{A}+4\theta _{B}\right)=0.2EI\theta _{A}+0.4EI\theta _{B}$

$M_{BC}={\frac {2EI}{L}}\left(4\theta _{B}+2\theta _{C}\right)=0.8EI\theta _{B}+0.4EI\theta _{C}$

$M_{CB}={\frac {2EI}{L}}\left(2\theta _{B}+4\theta _{C}\right)=0.4EI\theta _{B}+0.8EI\theta _{C}$

$M_{CD}={\frac {EI}{L}}\left(4\theta _{C}\right)=0.4EI\theta _{C}$

$M_{DC}={\frac {EI}{L}}\left(2\theta _{C}\right)=0.2EI\theta _{C}$

تعادل در گره ها

به دلیل اینکه سه مجهول مسئله دوران در گره‌های C، B، A هستند کافی است تعادل لنگر در این گره‌ها را بنویسیم که سه معادله به ما می‌دهد:

$\Sigma M_{A}=M_{AB}+M_{AB}^{f}=0.4EI\theta _{A}+0.2EI\theta _{B}-14.7=0$

$\Sigma M_{B}=M_{BA}+M_{BA}^{f}+M_{BC}+M_{BC}^{f}=0.2EI\theta _{A}+1.2EI\theta _{B}+0.4EI\theta _{C}-2.033=0$

$\Sigma M_{C}=M_{CB}+M_{CB}^{f}+M_{CD}+M_{CD}^{f}=0.4EI\theta _{B}+1.2EI\theta _{C}-4.167=0$

مقدار دوران ها

با حل دستگاه سه معادله و سه مجهول بالا مقادیر دوران‌ها به صورت زیر به دست می آید:

$\theta _{A}={\frac {40.219}{EI}}$

$\theta _{B}={\frac {-6.937}{EI}}$

$\theta _{C}={\frac {5.785}{EI}}$

مقادیر لنگر در انتهای اعضا

با جایگذاری مقادیر به دست آمده در معادلات شیب افت مقادیر لنگر در انتهای اعضا به دست می آید:

$M_{AB}=0.4\times 40.219+0.2\times \left(-6.937\right)-14.7=0$

$M_{BA}=0.2\times 40.219+0.4\times \left(-6.937\right)+6.3=11.57$

$M_{BC}=0.8\times \left(-6.937\right)+0.4\times 5.785-8.333=-11.57$

$M_{CB}=0.4\times \left(-6.937\right)+0.8\times 5.785+8.333=10.19$

$M_{CD}=0.4\times 5.785-12.5=-10.19$

$M_{DC}=0.2\times 5.785+12.5=13.66$

منابع

• Norris, Charles Head (1976). Elementary Structural Analysis (3rd ed.). McGraw-Hill. pp. 313–326. ISBN 0-07-047256-4. {{cite book}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
• McCormac, Jack C. (1997). Structural Analysis: A Classical and Matrix Approach (2nd ed.). Addison-Wesley. pp. 430–451. ISBN 0-673-99753-7. {{cite book}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
• Yang, Chang-hyeon (2001-01-10). Structural Analysis (به کره‌ای) (4th ed.). Seoul: Cheong Moon Gak Publishers. pp. 357–389. ISBN 89-7088-709-1. Archived from the original on 8 October 2007. Retrieved 16 May 2012.

جستارهای وابسته

• تئوری تیرها
• روش توزیع لنگر