روش ثابت زمانی مدار باز

روش ثابت زمانی مدار باز (به انگلیسی: open-circuit time constant) (OCT) یک فنّ تحلیل تقریبی است که در طراحی مدارهای الکترونیکی برای تعیین فرکانس گوشه مدارهای پیچیده استفاده می‌شود. این یک مورد خاص از روش ثابت زمانی با مقدار-صفر (ZVT) است که عناصر راکتیو فقط از خازنها تشکیل می‌شوند. روش ثابت زمان مقدار-صفر (ZVT) خود یک مورد خاص از تحلیل عمومی ثابت زمانی و انتقالی (TTC) است که امکان ارزیابی کامل صفرها و قطب‌های هر سیستم LTI فشرده را با هر دو سلف و خازن به عنوان عناصر راکتیو فراهم می‌کند. استفاده از ثابت‌های زمانی و ثابت‌های انتقال روش OCT ارزیابی سریعی را ارائه می‌کند و بیشترین سهم را در ثابت‌های زمانی به عنوان راهنمای بهبود مدار شناسایی می‌کند.

اساس روش تقریبی است که فرکانس گوشه تقویت‌کننده با جمله‌ای در مخرج تابع انتقال آن که با فرکانس خطی است تعیین می‌شود. این تقریب می‌تواند در برخی موارد که یک صفر در صورت‌کسر از نظر فرکانس نزدیک است، بسیار نادرست باشد.^[۱] اگر همه قطب‌ها حقیقی باشند و هیچ صفری وجود نداشته باشد، این تقریب همیشه پایستار است، به این معنا که معکوس مجموع ثابت‌های زمانی صفر کمتر از فرکانس گوشه واقعی مدار است.^[۲]

این روش همچنین از یک روش ساده شده برای یافتن عبارت خطی در فرکانس بر اساس جمع کردن حاصل‌ضرب RC برای هر خازن در مدار استفاده می‌کند، که در آن مقاومت R برای یک خازن انتخابی، مقاومتی است که با قرار دادن یک منبع آزمون در محل آن و قراردادن تمام خازن‌های دیگر به صفر، آن پیدا می‌شود. از این رو نام فنّ ثابت زمانی با مقدار صفر است.

مثال: شبکه RC ساده

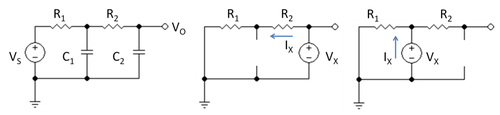
شکل ۱ یک فیلتر پایین‌گذر RC ساده را نشان می‌دهد. تابع انتقال آن با استفاده از قانون جریان کریشف به شرح زیر است. در خروجی،

{\frac {V_{O}}{V_{S}}}={\frac {1}{1+j\omega \left(C_{2}(R_{1}+R_{2})+C_{1}R_{1}\right)+(j\omega )^{2}C_{1}C_{2}R_{1}R_{2}}}

که در آن V₁ ولتاژ روی خازن C ₁ است. در گره مرکزی:

\left(1+j\omega {\tau }_{1})(1+j\omega {\tau }_{2}\right)=1+j\omega \left(C_{2}(R_{1}+R_{2})+C_{1}R_{1}\right)+(j\omega )^{2}C_{1}C_{2}R_{1}R_{2}

با ترکیب این روابط تابع انتقال به صورت زیر به‌دست می‌آید:

\tau _{1}+\tau _{2}=C_{2}(R_{1}+R_{2})+C_{1}R_{1}\,

\tau _{1}\tau _{2}=C_{1}C_{2}R_{1}R_{2}\ .

عبارت خطی در j ω در این تابع انتقال را می‌توان با روش زیر به‌دست‌آورد که کاربرد روش ثابت زمانی مدار باز برای این مثال است.

منبع سیگنال را روی صفر قرار دهید.
خازن C₂ را انتخاب کنید، آن را با یک ولتاژ آزمون V_X جایگزین کنید و C₁ را با یک مدار باز جایگزین کنید. سپس مقاومت مشاهده شده توسط ولتاژ آزمون با استفاده از مدار در پانل میانی شکل ۱ پیدا می‌شود و به سادگی V_X/I_X = R₁ + R₂ است. حاصل‌ضرب C₂ (R₁ + R₂) را تشکیل دهید.
خازن C₁ را انتخاب کنید، آن را با یک ولتاژ آزمون V_X جایگزین کنید و C₂ را با یک مدار باز جایگزین کنید. سپس مقاومت مشاهده شده توسط ولتاژ آزمون با استفاده از مدار در پانل سمت راست شکل ۱ پیدا می‌شود و به سادگی V_X/I_X = R₁ است. حاصل‌ضرب C₁ R₁ را تشکیل دهید.
این جمله‌ها را جمع بزنید.

در واقع، گویی هر خازن از طریق مقاومت موجود در مدار، زمانی که خازن دیگر یک مدار باز است، شارژ و تخلیه می‌شود.

رویه ثابت زمان مدار باز، جمله خطی را در j ω ارائه می‌دهد، صرف نظر از اینکه شبکه RC چقدر پیچیده می‌شود. این در ابتدا با محاسبه ضرایب مشترک ماتریس ادمیتانس توسط تورنتون و سِرل توسعه و اثبات شد.^[۳] اثبات القایی شهودی‌تر این (و سایر ویژگی‌های TTC) بعداً توسط حاجی‌میری ایجاد شد.^[۴]

برای یک مدار پیچیده، این روش شامل پیروی از قوانین بالا، عبور از تمام خازن‌های مدار است. اشتقاق کلی تری در گری و مایر یافت می‌شود.^[۵]

تا اینجا نتیجه کلی است، اما تقریبی برای استفاده از این نتیجه معرفی شده است: این فرض وجود دارد که این عبارت خطی در jω فرکانس گوشه مدار را تعیین می‌کند.

این فرض را می‌توان با استفاده از مثال شکل ۱ دقیق تر بررسی کرد: فرض کنید ثابت‌های زمانی این مدار τ₁ و τ₂ باشد؛ یعنی:

\tau _{1}\approx {\hat {\tau _{1}}}=\ \tau _{1}+\tau _{2}=C_{2}(R_{1}+R_{2})+C_{1}R_{1}\,

با مقایسه ضرایب جمله‌های خطی و درجه دوم در j‌ω، نتیجه می‌شود:

\tau _{1}+\tau _{2}=C_{2}(R_{1}+R_{2})+C_{1}R_{1}\ ,

\tau _{1}\tau _{2}=C_{1}C_{2}R_{1}R_{2}\ .

یکی از دو ثابت زمانی طولانی‌ترین خواهد بود؛ فرض کنید τ₁ باشد. برای لحظه ای فرض کنید که τ₁ >> τ₂ بسیار بزرگتر از دیگری است، در این مورد، تقریب‌ها چنین است:

\tau _{2}={\frac {\tau _{1}\tau _{2}}{\tau _{1}}}\approx {\frac {\tau _{1}\tau _{2}}{\tau _{1}+\tau _{2}}}\ .

و

\tau _{2}\approx {\hat {\tau _{2}}}={\frac {\tau _{1}\tau _{2}}{\tau _{1}+\tau _{2}}}={\frac {C_{1}C_{2}R_{1}R_{2}}{C_{2}(R_{1}+R_{2})+C_{1}R_{1}}}\,

به عبارت دیگر، جایگذاری مقادیر RC:

f_{3dB}={\frac {1}{2\pi {\hat {\tau _{1}}}}}\,

و

{\frac {1}{(1+j\omega \tau _{1})(1+j\omega \tau _{2})}}\

\

با

\

\ {\frac {1}{(1+j\omega {\hat {\tau _{1}}})(1+j\omega {\hat {\tau _{2}}})}}\ .

که در آن (^) نتیجه تقریبی را نشان می‌دهد. علاوه بر این، توجه کنید که ثابت‌های زمان مدار هر دو خازن را شامل می‌شوند. به عبارت دیگر، به‌طور کلی ثابت‌های زمانی مدار توسط هیچ خازن منفردی تعیین نمی‌شوند. با استفاده از این نتایج، به راحتی می‌توان بررسی کرد که فرکانس گوشه (فرکانس ۳ دسی‌بل) چقدر خوب است که توسط رابطه زیر به‌دست می‌آید

f_{3dB}={\frac {1}{2\pi {\hat {\tau _{1}}}}}\,

چون پارامترها متفاوت است همچنین، تابع انتقال دقیق را می‌توان با یک تقریبی مقایسه کرد، یعنی،

{\frac {1}{(1+j\omega \tau _{1})(1+j\omega \tau _{2})}}\

\

با

\

\ {\frac {1}{(1+j\omega {\hat {\tau _{1}}})(1+j\omega {\hat {\tau _{2}}})}}\ .

البته سازشمندی زمانی خوب است که فرض τ₁ >> τ₂ دقیق باشد.

شکل ۲ تقریب را نشان می‌دهد. محور x نسبت τ₁/τ₂ در مقیاس لگاریتمی است. افزایش در این متغیر به این معنی است که قطب بالاتر، بالاتر از فرکانس گوشه است. محور y نسبت تخمین OCTC (ثابت زمانی مدار باز) به ثابت زمانی واقعی است. برای پایین‌ترین قطب از منحنی T_1 استفاده کنید. این منحنی به فرکانس گوشه اشاره دارد. و برای قطب بالاتر از منحنی T_2 استفاده کنید. بدترین سازشمندی برای τ₁ = τ₂ است. در این مورد ${\widehat {\tau }}_{1}=2\tau _{1}$ و فرکانس گوشه ضریب ۲ بسیار کوچک است. قطب بالاتر ضریب ۲ بسیار زیاد (ثابت زمانی آن نصف مقدار واقعی است) است.

در همه موارد، فرکانس گوشه تخمینی نزدیکتر از ضریب دو از فرکانس واقعی است، و همیشه محافظه‌کارانه است، یعنی کمتر از گوشه واقعی، بنابراین مدار واقعی بهتر از حد پیش‌بینی شده رفتار خواهد کرد. با این حال، قطب بالاتر همیشه خوش‌بینانه است، یعنی قطب بالا را در فرکانس بالاتری از آنچه واقعاً وجود دارد، پیش‌بینی می‌کند. برای استفاده از این تخمین‌ها برای پیش‌بینی پاسخ پله، که به نسبت فرکانس دو قطب بستگی دارد (به عنوان مثال به مقاله در مورد دوپاره‌سازی قطب مراجعه کنید)، شکل ۲ نشان می‌دهد که نسبت نسبتاً بزرگی از τ₁/τ₂ برای دقت مورد نیاز است زیرا خطاها در ${\widehat {\tau }}_{1}$ و ${\widehat {\tau }}_{2}$ یکدیگر را در نسبت ${\widehat {\tau }}_{1}/{\hat {\tau }}_{2}$ تقویت می‌کنند.

روش ثابت زمانی مدار باز به تنهایی بر فرکانس گوشه تمرکز می‌کند، اما همان‌طور که در بالا مشاهده شد، تخمین برای قطب‌های بالاتر نیز امکان‌پذیر است.

کاربرد روش ثابت زمان مدار باز برای تعدادی از طبقات تقویت‌کننده تک ترانزیستوری را می‌توان در پیتت و کانداسوامی یافت.^[۶]

مراجع و یادداشت‌ها

↑ Marc T. Thompson (2006). Intuitive analog circuit design: a problem solving approach using design case studies. Oxford UK/ Amsterdam: Elsevier/Newnes. p. Chapter 7; p.161–167. ISBN 0-7506-7786-4.
↑ Hong, Brian; Hajimiri, Ali (August 2016). "Upper and lower bounds on a system's bandwidth based on its zero-value time constants" (PDF). Electronics Letters. 52 (16): 1383–1385. doi:10.1049/el.2016.1724.
↑ Richard D. Thornton & Campbell L. Searle (1965). Multistage transistor circuits (First ed.). New York: Wiley.
↑ Hajimiri, Ali (June 2010). "Generalized time-and transfer-constant circuit analysis" (PDF). IEEE Transactions on Circuits and Systems I: Regular Papers. 57 (6): 1105–1121. doi:10.1109/TCSI.2009.2030092.
↑ Paul R. Gray, Hurst P J Lewis S H & Meyer RG (2001). Analysis and design of analog integrated circuits (Fourth ed.). New York: Wiley. p. §7.3.2 pp. 517–520. ISBN 0-471-32168-0.
↑ Andre Pittet & A. Kandaswamy (2005). Analog electronics. New Delhi: Prentice-Hall of India. p. Chapter 4; pp. 155–166. ISBN 81-203-2784-5.

[Thompson2-1] Marc T. Thompson (2006). Intuitive analog circuit design: a problem solving approach using design case studies. Oxford UK/ Amsterdam: Elsevier/Newnes. p. Chapter 7; p.161–167. ISBN 0-7506-7786-4.

[Hong-2] Hong, Brian; Hajimiri, Ali (August 2016). "Upper and lower bounds on a system's bandwidth based on its zero-value time constants" (PDF). Electronics Letters. 52 (16): 1383–1385. doi:10.1049/el.2016.1724.

[Thornton-Searle2-3] Richard D. Thornton & Campbell L. Searle (1965). Multistage transistor circuits (First ed.). New York: Wiley.

[Hajimiri-4] Hajimiri, Ali (June 2010). "Generalized time-and transfer-constant circuit analysis" (PDF). IEEE Transactions on Circuits and Systems I: Regular Papers. 57 (6): 1105–1121. doi:10.1109/TCSI.2009.2030092.

[Gray-Meyer2-5] Paul R. Gray, Hurst P J Lewis S H & Meyer RG (2001). Analysis and design of analog integrated circuits (Fourth ed.). New York: Wiley. p. §7.3.2 pp. 517–520. ISBN 0-471-32168-0.

[Pittet2-6] Andre Pittet & A. Kandaswamy (2005). Analog electronics. New Delhi: Prentice-Hall of India. p. Chapter 4; pp. 155–166. ISBN 81-203-2784-5.

[۱]

[۲]

[۳]

[۴]

[۵]

[۶]