راهزن چند دست

در تئوری احتمالات و یادگیری ماشین ، مسئله راهزن چند دست مسئلهای است که در آن مجموعه محدود ثابتی از منابع باید بین گزینههای رقیب تخصیص داده شود. انتخابها به گونهای که سود مورد انتظار آنها را به حداکثر برساند، زمانی که ویژگیهای هر انتخاب در زمان تخصیص فقط تا حدی شناخته شده است و ممکن است با گذشت زمان یا با تخصیص منابع به آن انتخاب، بهتر شناخته شود. </ref> این یک مسئله کلاسیک یادگیری تقویتی است که مسئله معاوضه اکتشاف – بهره برداری را توصیف میزند. این نام از تصور یک قمارباز در ردیف دستگاههای بازی گرفته شده است، که باید تصمیم بگیرد که با کدام دستگاهها بازی کند، هر دستگاه را چند مرتبه بازی کند و به چه ترتیبی بازی کند، و آیا با دستگاه فعلی ادامه دهد یا دستگاه دیگری را امتحان کند. [۱] مسئله راهزن چند دست در دستهبندی برنامهریزی تصادفی قرار میگیرد.
در این مسئله، هر دستگاه یک پاداش تصادفی را از یک توزیع احتمال خاص برای آن دستگاه ارائه میکند، که این توزیع از قبل مشخص نیست. هدف قمارباز به حداکثر رساندن مجموع پاداشهای به دست آمده از طریق دنبالهای از کشیدن اهرمها است. [۲] [۳] معاوضه اساسیای که قمارباز در هر آزمایشی با آن روبرو میشود، بین «استثمار» از دستگاهی است که بالاترین بازدهی مورد انتظار را دارد و «اکتشاف» برای به دست آوردن اطلاعات بیشتر در مورد بازدهی مورد انتظار دستگاههای دیگر است. مبادله بین اکتشاف و بهرهبرداری در یادگیری ماشین بررسی شده است. در عمل، راهزن چند دست برای مدلسازی مسائلی مانند مدیریت پروژههای تحقیقاتی در یک سازمان بزرگ، مانند یک بنیاد علمی یا یک شرکت داروسازی، استفاده شده است. [۲] [۳] در نسخههای اولیه مسئله، قمارباز بدون هیچ دانش اولیه در مورد دستگاهها شروع میکند.
هربرت رابینز در سال 1952، با درک اهمیت مسئله، استراتژیهای انتخاب جمعیت همگرا را در "برخی از جنبههای طراحی متوالی آزمایشها" ساخت. [۴] یک قضیه، شاخص گیتینز ، که برای اولین بار توسط جان سی منتشر شد، یک سیاست بهینه برای به حداکثر رساندن پاداش مورد انتظار ارائه میدهد. [۵]
انگیزه تجربی
[ویرایش]
مسئله راهزن چند دست، عاملی را مدل میکند که به طور همزمان تلاش میکند دانش جدیدی («اکتشاف») به دست آورد و تصمیمات خود را بر اساس دانش موجود («استثمار») بهینه کند. عامل تلاش میکند تا این دو وظیفه رقابتی را متعادل کند تا ارزش کلی آنها را در بازه زمانی در نظر گرفته شده به حداکثر برساند. کاربردهای عملی زیادی از مسئله راهزن وجود دارد، به عنوان نمونه:
- کارآزماییهای بالینی که اثرات درمانهای تجربی مختلف را در عین به حداقل رساندن تلفات بیمار بررسی میکنند، [۲] [۳] [۶] [۷]
- تلاشهای مسیریابی تطبیقی برای به حداقل رساندن تاخیر در شبکه،
- طراحی سبد مالی [۸] [۹]
در این مثالهای عملی، مسئله مستلزم رسیدن به حداکثر پاداش بر اساس دانشی است که قبلاً به دست آوردهایم و تلاش برای اقدامات جدید برای افزایش بیشتر دانش است. این به عنوان معاوضه بهره برداری در مقابل اکتشاف در یادگیری ماشینی شناخته میشود.
این مدل برای کنترل تخصیص پویای منابع به پروژههای مختلف استفاده شده است و به این سؤال پاسخ میدهد که با توجه به عدم اطمینان در مورد دشواری و بازدهی هر گزینه، روی کدام پروژه کار شود. [۱۰]
این مسئله در ابتدا توسط دانشمندان متفقین در جنگ جهانی دوم مورد توجه قرار گرفت، اما به قدری غیرقابل حل بود که به گفته پیتر ویتل ، پیشنهاد شد که این مسئله در بین آلمانیها رها شود تا دانشمندان آلمانی نیز بتوانند وقت خود را برای آن تلف کنند. [۱۱]
نسخهای از مسئله که اکنون معمولاً مورد بررسی قرار میگیرد توسط هربرت رابینز در سال 1952 فرموله شده است.
مدل راهزن چند دستی
[ویرایش]راهزن چند دستی (کوتاه: MAB) را میتوان به عنوان مجموعه ای از توزیعهای واقعی دید. ، هر توزیع با پاداشهای ارائه شده توسط یکی از اهرم مرتبط است. اگر مقادیر میانگین مرتبط با این توزیعهای پاداش باشد، قمارباز به طور مکرر در هر دور یک اهرم بازی میکند و پاداش مربوطه را مشاهده میکند. هدف این است که مجموع پاداشهای جمع آوری شده را به حداکثر برساند. افق تعداد دورهایی است که باید انجام شود. مسئله راهزن به طور رسمی معادل فرآیند تصمیم گیری مارکوف یک حالته است. پشیمانی بعد از دور به عنوان تفاوت مورد انتظار بین مجموع پاداش مرتبط با یک استراتژی بهینه و مجموع پاداشهای جمع آوری شده تعریف میشود:
،
جایی که حداکثر میانگین پاداش است، ، و پاداش در دور t است.
استراتژی صفر پشیمانی استراتژی است که میانگین پشیمانی آن در هر راند وقتی تعداد دورهای بازی شده به بی نهایت میل میکند با احتمال 1 به صفر میل میکند. به طور شهودی، استراتژیهای بدون پشیمانی تضمین میشوند که اگر راندهای کافی بازی شوند، به یک استراتژی بهینه (الزاماً منحصربهفرد) همگرا میشوند.
تغییرات
[ویرایش]یک فرمول متداول، راهزن چند دست دودویی یا راهزن چند دست برنولی است که یک جایزه با احتمال صادر میکند و در غیر این صورت پاداش صفر است.
فرمول دیگری از راهزن چند دشت دارای هر اهرم نشان دهنده یک ماشین مارکوف مستقل است. هر بار که دستگاه خاصی بازی میشود، وضعیت آن دستگاه به دستگاه جدیدی میرود که بر اساس احتمالات تکامل حالت مارکوف انتخاب میشود. بسته به وضعیت فعلی دستگاه یک پاداش وجود دارد. در یک تعمیم به نام "مسئله راهزن بیقرار"، حالتهای دستگاههای بازی نشده نیز می تواند در طول زمان تکامل یابد. [۱۲] همچنین در مورد سیستمهایی که تعداد انتخابها (در مورد اینکه کدام دستگاه بازی شود) در طول زمان افزایش مییابد، بحث شده است. [۱۳]
محققان علوم کامپیوتر راهزنان چند دست را تحت بدترین مفروضات (worst-case) مورد مطالعه قرار دادهاند و الگوریتمهایی را برای به حداقل رساندن پشیمانی در زمانی متناهی و نامتناهی برای بازدهی اهرمهای تصادفی [۱۴] و غیر تصادفی [۱۵] به دست آوردهاند.
استراتژیهای راهزن
[ویرایش]یک پیشرفت بزرگ، ایجاد استراتژیها یا سیاستهای انتخاب بهینه جمعیت (که دارای حداکثر نرخ همگرایی یکنواخت با جمعیت با بالاترین میانگین هستند) در کار شرح داده شده در زیر است.
راه حلهای بهینه
[ویرایش]در مقاله "قوانین تخصیص تطبیقی کارآمد مجانبی"، لای و رابینز [۱۶] (به دنبال مقالات رابینز و همکارانش که به رابینز در سال 1952 بازمیگردند) سیاستهای انتخاب جمعیت همگرا را ارائه کردند که سریعترین نرخ همگرایی را (به جمعیت با بالاترین میانگین) برای حالتی که توزیع پاداش جمعیت خانواده نمایی یک پارامتری است، دارد. سپس در کاتهاکیس و رابینز [۱۷] سادهسازی خطمشی و اثبات اصلی برای مورد جمعیتهای عادی با واریانسهای شناخته شده ارائه شد. پیشرفت قابل توجه بعدی توسط Burnetas و Katehakis در مقاله "سیاستهای تطبیقی بهینه برای مسائل تخصیص متوالی"، [۱۸] به دست آمد، جایی که سیاستهای مبتنی بر شاخص با حداکثر نرخ همگرایی یکنواخت، تحت شرایط عمومی تر که شامل مواردی است که در آن توزیعها وجود دارد، ساخته شد. نتایج هر جمعیت به بردار پارامترهای ناشناخته بستگی دارد. Burnetas و Katehakis همچنین یک راه حل صریح برای مورد مهمی ارائه کردند که در آن توزیع نتایج از توزیعهای گسسته و تکمتغیره دلخواه (یعنی ناپارامتریک) پیروی میکند.
بعداً در «سیاستهای تطبیقی بهینه برای فرآیندهای تصمیم مارکوف» [۱۹] بورنتاس و کاتهاکیس مدل بسیار بزرگتری از فرآیندهای تصمیمگیری مارکوف را تحت اطلاعات محدود مطالعه کردند، جایی که قانون گذار و/یا پاداش یک دوره ممکن است به پارامترهای ناشناخته بستگی داشته باشد. در این کار، نویسندگان یک فرم صریح برای یک کلاس از سیاستهای تطبیقی با ویژگیهای نرخ همگرایی حداکثری یکنواخت برای کل پاداش افق محدود مورد انتظار تحت مفروضات کافی فضاهای کنش حالت محدود و کاهشناپذیری قانون گذار ارائه کردند. یکی از ویژگیهای اصلی این سیاستها این است که انتخاب اقدامات، در هر حالت و دوره زمانی، بر اساس شاخصهایی است که تورمهای سمت راست معادلات میانگین تخمینی بهینه پاداش هستند. این تورمها اخیراً در کار تواری و بارتلت، [۲۰] اورتنر [۲۱] فیلیپی، کاپی، و گاریویه [۲۲] و هوندا و تاکمورا، رویکرد خوشبینانه نامیده میشوند. [۲۳]
برای راهزنان چند دست برنولی، پیلارسکی و همکاران روشهای محاسباتی استخراج راهحلهای کاملاً بهینه (نه فقط مجانبی) را با استفاده از برنامهنویسی پویا در مقاله "سیاست بهینه برای راهزنان برنولی: محاسبات و الگوریتم" مطالعه کردند. [۲۴] این کار از طریق طرحهای نمایهسازی، جداول جستجو و سایر تکنیکها، راهحلهای بهینه عملاً قابل اجرا را برای راهزنان برنولی ارائه کرد، مشروط بر اینکه افقهای زمانی و تعداد اهرمها بیش از حد بزرگ نشوند. پیلارسکی و همکاران بعداً این کار را در "پاداش تاخیری راهزنان برنولی: سیاست بهینه و متاالگوریتم پیش بینی کننده PARDI" [۲۵] گسترش داد تا روشی برای تعیین خط مشی بهینه راهزنان برنولی ایجاد کند، زمانی که پاداش ممکن است بلافاصله پس از یک تصمیم آشکار نشود و ممکن است به تاخیر بیفتد. این روش بر محاسبه مقادیر مورد انتظار نتایج پاداش که هنوز آشکار نشده اند و بهروزرسانی توزیع احتمالات پسین هنگام آشکار شدن پاداشها متکی است.
میتوان راه حلهای بهینه برای راهزن چند دست [۲۶] برای استخراج ارزش انتخابهای حیوانات استفاده کرد. فعالیت نورونها در آمیگدال و جسم مخطط شکمی مقادیر به دست آمده از این سیاستها را رمزگذاری میکند و میتواند برای رمزگشایی زمانی که حیوانات انتخابهای اکتشافی در مقابل استثماری انجام دهند استفاده شود. علاوه بر این، سیاستهای بهینه رفتار انتخاب حیوانات را بهتر از استراتژیهای جایگزین پیشبینی میکنند (که در زیر توضیح داده شده است). این نشان میدهد که راهحلهای بهینه برای مسئله راهزن چند دست از نظر بیولوژیکی قابل قبول هستند. [۲۷]
- UCBC (محدودههای بالای اطمینان تاریخی با خوشهها): الگوریتم UCB را برای یک تنظیم جدید به گونه ای تطبیق میدهد که بتواند هم خوشه بندی و هم اطلاعات تاریخی را در خود جای دهد. این الگوریتم مشاهدات تاریخی را با استفاده از هر دو در محاسبه پاداش میانگین مشاهده شده و عبارت عدم قطعیت ترکیب میکند. این الگوریتم اطلاعات خوشهبندی را با بازی در دو سطح ترکیب میکند: ابتدا انتخاب یک خوشه با استفاده از یک استراتژی شبیه به UCB در هر مرحله زمانی، و متعاقبا انتخاب یک اهرم از درون خوشه، دوباره با استفاده از یک استراتژی مشابه UCB.
راه حلهای تقریبی
[ویرایش]راهبردهای زیادی وجود دارند که راه حل تقریبی برای مسئله راهزن ارائه میدهند و میتوان آنها را در چهار گروه کلی که در زیر شرح داده شده است قرار داد:
استراتژیهای نیمه یکنواخت
[ویرایش]استراتژیهای نیمه یکنواخت اولین (و سادهترین) استراتژیهایی بودند که برای حل تقریبی مسئله راهزن کشف شدند. همه آن استراتژیها رفتار حریصانهای دارند که در آن بهترین اهرم (بر اساس مشاهدات قبلی) همیشه کشیده میشود، مگر زمانی که یک اقدام تصادفی (یکنواخت) انجام شود.
- استراتژی اپسیلون حریص : [۲۸] بهترین اهرم برای نسبت از آزمایشها انتخاب میشود، و یک اهرم به طور تصادفی (با احتمال یکنواخت) برای یک نسبت انتخاب میشود. یک مقدار پارامتر متداول ممکن است باشد، اما بسته به شرایط و تمایلات میتواند بسیار متفاوت باشد.
- استراتژی اپسیلون اول[نیازمند منبع] : مرحله اکتشاف خالص با مرحله بهره برداری خالص دنبال میشود. برای آزمایش در مجموع، مرحله اکتشاف آزمایشها را اشغال میکند و مرحله بهره برداری آزمایش. در طول مرحله اکتشاف، یک اهرم به طور تصادفی انتخاب میشود (با احتمال یکنواخت). در طول مرحله بهره برداری، بهترین اهرم همیشه انتخاب میشود.
- استراتژی کاهش اپسیلون[نیازمند منبع] : شبیه به استراتژی epsilon-greedy، با این تفاوت که ارزش با پیشرفت آزمایش کاهش مییابد و در نتیجه رفتار بسیار اکتشافی در شروع و رفتار بسیار استثمارگرانه در پایان ایجاد میشود.
- استراتژی تطبیقی حریصانه-اپسیلون بر اساس تفاوتهای ارزشی (VDBE) : مشابه استراتژی کاهش اپسیلون است، با این تفاوت که اپسیلون بر اساس پیشرفت یادگیری به جای تنظیم دستی کاهش مییابد (Tokic، 2010). [۲۹] نوسانات زیاد در برآورد ارزش، منجر به اپسیلون بالا (اکتشاف زیاد، بهره برداری کم) میشود. نوسانات کم به یک اپسیلون کم (اکتشاف کم، بهره برداری زیاد) منجر میشود. بهبودهای بیشتر را میتوان با انتخاب کنش با وزن نرم افزار در مورد اقدامات اکتشافی به دست آورد ( Tokic & Palm, 2011). [۳۰]
- استراتژی تطبیقی epsilon-greedy مبتنی بر گروههای بیزی (Epsilon-BMC) : یک استراتژی انطباق اپسیلون تطبیقی برای یادگیری تقویتی مشابه VBDE، با تضمینهای همگرایی یکنواخت است. در این چارچوب، پارامتر اپسیلون بهعنوان انتظار توزیع پسینی در نظر گرفته میشود که وزن یک عامل حریص (که کاملاً به پاداش آموخته شده اعتماد دارد) و عامل یادگیری یکنواخت (که به پاداش آموخته شده بیاعتماد است) دارد. این توزیع پسین با استفاده از یک توزیع بتا مناسب با فرض نرمال بودن پاداشهای مشاهده شده تقریب زده میشود. به منظور پرداختن به خطر احتمالی کاهش سریع اپسیلون، عدم قطعیت در واریانس پاداش آموخته شده نیز با استفاده از یک مدل گامای نرمال مدلسازی و بهروزرسانی میشود. (گیملفارب و همکاران، 2019). [۳۱]
- استراتژی متنی-اپسیلون-حریصانه: مشابه استراتژی اپسیلون-حریصانه، با این تفاوت که ارزش با توجه به وضعیت در فرآیندهای آزمایشی محاسبه میشود، که به الگوریتم اجازه میدهد Context-Aware باشد. این مبتنی بر اکتشاف/استثمار پویا است و میتواند با تصمیمگیری اینکه کدام موقعیت برای اکتشاف یا بهرهبرداری مناسبتر است، به طور انطباقی بین دو جنبه تعادل برقرار کند، که منجر به رفتار بسیار اکتشافی زمانی که موقعیت بحرانی نیست و رفتار بسیار استثمارگرانه در موقعیت بحرانی میشود. [۳۲]
استراتژیهای تطبیق احتمال
[ویرایش]استراتژیهای تطبیق احتمال این ایده را منعکس میکند که تعداد کشیدنها برای یک اهرم معین باید با احتمال واقعی آن برای بهینه بودن اهرم مطابقت داشته باشد. استراتژیهای تطبیق احتمال نیز بهعنوان نمونهگیری تامپسون یا راهزنان بیزی شناخته میشوند، [۳۳] [۳۴] و اگر بتوانید از توزیع پسین برای مقدار میانگین هر جایگزین نمونه برداری کنید، بهطور شگفتآوری آسان میشوند.
استراتژیهای قیمت گذاری
[ویرایش]استراتژیهای قیمت گذاری قیمتی را برای هر اهرم تعیین میکنند. به عنوان مثال، همانطور که با الگوریتم POKER نشان داده شده است، [۳۵] قیمت میتواند مجموع پاداش مورد انتظار به اضافه تخمینی از پاداشهای اضافی آینده باشد که از طریق دانش اضافی به دست میآید. اهرم بالاترین قیمت همیشه کشیده میشود.
راهزن زمینهای
[ویرایش]یک تعمیم مفید از راهزن چند دست، راهزن چند دست زمینهای است. در هر تکرار، یک عامل هنوز باید بین اهرمها انتخاب کند، اما همچنین یک بردار ویژگی d بعدی را میبیند، بردار زمینه ای که میتواند همراه با پاداش اهرمهای بازی شده در گذشته برای انتخاب اهرم بازی استفاده کند. با گذشت زمان، هدف یادگیرنده جمعآوری اطلاعات کافی در مورد چگونگی ارتباط بردارهای زمینه و پاداشها با یکدیگر است، به طوری که بتواند بهترین اهرم بعدی را با نگاه کردن به بردارهای ویژگی پیشبینی کند. [۳۶]
راه حلهای تقریبی برای راهزن زمینهای
[ویرایش]استراتژیهای زیادی وجود دارند که راهحلی تقریبی برای مسئله راهزن زمینهای ارائه میدهند و میتوان آنها را در دو دسته کلی به تفصیل در زیر قرار داد.
راهزنان خطی آنلاین
[ویرایش]- الگوریتم LinUCB (محدوده اطمینان بالا) : نویسندگان یک وابستگی خطی بین پاداش مورد انتظار یک عمل و زمینه آن فرض میکنند و فضای نمایش را با استفاده از مجموعهای از پیشبینیکنندههای خطی مدل میکنند. [۳۷] [۳۸]
- الگوریتم LinRel (یادگیری تقویتی انجمنی خطی) : شبیه LinUCB است، اما از تجزیه ارزش تکی به جای رگرسیون Ridge برای به دست آوردن تخمینی از اطمینان استفاده میکند.
- HLINUCBC (LINUCB تاریخی با خوشهها) : پیشنهاد شده در مقاله، ایده LinUCB را با اطلاعات تاریخی و خوشهبندی گسترش میدهد.
راهزنان غیر خطی آنلاین
[ویرایش]- الگوریتم UCBogram : توابع پاداش غیرخطی با استفاده از یک برآوردگر ثابت تکه ای به نام رگرسیون در رگرسیون ناپارامتریک تخمین زده میشوند. سپس، UCB روی هر قطعه ثابت استفاده میشود. اصلاحات متوالی پارتیشن فضای زمینه به صورت تطبیقی برنامه ریزی یا انتخاب میشوند. [۳۹] [۴۰] [۴۱]
- الگوریتمهای خطی تعمیمیافته : توزیع پاداش از یک مدل خطی تعمیمیافته پیروی میکند، توسعهای برای راهزنهای خطی. [۴۲] [۴۳] [۴۴] [۴۵]
- الگوریتم NeuralBandit : در این الگوریتم چندین شبکه عصبی برای مدلسازی ارزش پاداشها با دانستن زمینه آموزش داده میشوند و از یک رویکرد چند متخصص برای انتخاب آنلاین پارامترهای پرسپترونهای چند لایه استفاده میکنند. [۴۶]
- الگوریتم KernelUCB : یک نسخه غیرخطی هستهای از linearUCB، با پیادهسازی کارآمد و تحلیل زمان محدود. [۴۷]
- الگوریتم جنگل راهزن : یک جنگل تصادفی با دانستن توزیع مشترک زمینهها و پاداشها در جنگل تصادفی ساخته شده و تحلیل میشود. [۴۸]
- الگوریتم مبتنی بر اوراکل : این الگوریتم مسئله راهزن زمینه ای را به یک سری مسائل یادگیری نظارت شده کاهش میدهد و بر فرض تحقق پذیری معمولی در تابع پاداش متکی نیست. [۴۹]
راهزن زمینهای محدود
[ویرایش]- راهزنان توجه زمینهای یا راهزن زمینهای با زمینه محدود : [۵۰] نویسندگان فرمول جدیدی از مدل راهزن چند دست را در نظر میگیرند، که راهزن زمینهای با زمینه محدود نامیده میشود، که در آن تنها تعداد محدودی از ویژگیها توسط آموزنده قابل دسترسی است. هر تکرار این فرمول جدید ناشی از مسائل آنلاین مختلف است که در آزمایشهای بالینی، سیستمهای توصیهکننده و مدلسازی توجه به وجود میآیند. در اینجا، آنها الگوریتم راهزن استاندارد چند دستی معروف به نمونهبرداری تامپسون را برای استفاده از تنظیمات زمینه محدود تطبیق میدهند و دو الگوریتم جدید به نامهای نمونهبرداری تامپسون با زمینه محدود (TSRC) و نمونهبرداری تامپسون ویندوز با زمینه محدود (WTSRC) را پیشنهاد میکنند. ، به ترتیب برای جابجایی محیطهای ثابت و غیر ثابت.
در عمل، معمولاً هزینه ای مرتبط با منابع مصرف شده توسط هر اقدام وجود دارد و هزینه کل توسط بودجه در بسیاری از کاربردها مانند جمع سپاری و آزمایشهای بالینی محدود میشود. راهزن زمینهای محدود (CCB) چنین مدلی است که هم محدودیتهای زمانی و هم بودجه را در یک محیط راهزن چند دست در نظر میگیرد. A. Badanidiyuru و همکاران. [۵۱] ابتدا راهزنهای زمینهای را با محدودیتهای بودجه مورد مطالعه قرار داد، که به آنها راهزنهای زمینهای منبع نیز میگویند و نشان داد که پشیمانی دست یافتنی است با این حال، کار آنها بر روی مجموعه محدودی از سیاستها متمرکز است و الگوریتم از نظر محاسباتی ناکارآمد است.
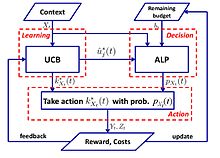
یک الگوریتم ساده با پشیمانی لگاریتمی در موارد زیر پیشنهاد شده است: [۵۲]
جستارهای وابسته
[ویرایش]- شاخص گیتینز - یک استراتژی قدرتمند و کلی برای بررسی مسئله راهزن.
- الگوریتم حریص
- توقف بهینه
- نظریه جستجو
- برنامه ریزی تصادفی
منابع
[ویرایش]- ↑ Weber, Richard (1992), "On the Gittins index for multiarmed bandits", Annals of Applied Probability, 2 (4): 1024–1033, doi:10.1214/aoap/1177005588, JSTOR 2959678
- ↑ ۲٫۰ ۲٫۱ ۲٫۲ Gittins, J. C. (1989), Multi-armed bandit allocation indices, Wiley-Interscience Series in Systems and Optimization., Chichester: John Wiley & Sons, Ltd., ISBN 978-0-471-92059-5
- ↑ ۳٫۰ ۳٫۱ ۳٫۲ Berry, Donald A.; Fristedt, Bert (1985), Bandit problems: Sequential allocation of experiments, Monographs on Statistics and Applied Probability, London: Chapman & Hall, ISBN 978-0-412-24810-8
- ↑ Robbins, H. (1952). "Some aspects of the sequential design of experiments". Bulletin of the American Mathematical Society. 58 (5): 527–535. doi:10.1090/S0002-9904-1952-09620-8.
- ↑ J. C. Gittins (1979). "Bandit Processes and Dynamic Allocation Indices". Journal of the Royal Statistical Society. Series B (Methodological). 41 (2): 148–177. doi:10.1111/j.2517-6161.1979.tb01068.x. JSTOR 2985029.
- ↑ Press, William H. (2009), "Bandit solutions provide unified ethical models for randomized clinical trials and comparative effectiveness research", Proceedings of the National Academy of Sciences, 106 (52): 22387–22392, Bibcode:2009PNAS..10622387P, doi:10.1073/pnas.0912378106, PMC 2793317, PMID 20018711.
- ↑ Press (1986)
- ↑ Brochu, Eric; Hoffman, Matthew W.; de Freitas, Nando (September 2010), Portfolio Allocation for Bayesian Optimization, arXiv:1009.5419, Bibcode:2010arXiv1009.5419B
- ↑ Shen, Weiwei; Wang, Jun; Jiang, Yu-Gang; Zha, Hongyuan (2015), "Portfolio Choices with Orthogonal Bandit Learning", Proceedings of International Joint Conferences on Artificial Intelligence (IJCAI2015), archived from the original on 4 December 2021, retrieved 30 January 2023
- ↑ Farias, Vivek F; Ritesh, Madan (2011), "The irrevocable multiarmed bandit problem", Operations Research, 59 (2): 383–399, doi:10.1287/opre.1100.0891
- ↑ Whittle, Peter (1979), "Discussion of Dr Gittins' paper", Journal of the Royal Statistical Society, Series B, 41 (2): 148–177, doi:10.1111/j.2517-6161.1979.tb01069.x
- ↑ Whittle, Peter (1988), "Restless bandits: Activity allocation in a changing world", Journal of Applied Probability, 25A: 287–298, doi:10.2307/3214163, JSTOR 3214163, MR 0974588
- ↑ Whittle, Peter (1981), "Arm-acquiring bandits", Annals of Probability, 9 (2): 284–292, doi:10.1214/aop/1176994469
- ↑ Auer, P.; Cesa-Bianchi, N.; Fischer, P. (2002). "Finite-time Analysis of the Multiarmed Bandit Problem". Machine Learning. 47 (2/3): 235–256. doi:10.1023/A:1013689704352.
- ↑ Auer, P.; Cesa-Bianchi, N.; Freund, Y.; Schapire, R. E. (2002). "The Nonstochastic Multiarmed Bandit Problem". SIAM J. Comput. 32 (1): 48–77. CiteSeerX 10.1.1.130.158. doi:10.1137/S0097539701398375.
- ↑ Lai, T.L.; Robbins, H. (1985). "Asymptotically efficient adaptive allocation rules". Advances in Applied Mathematics. 6 (1): 4–22. doi:10.1016/0196-8858(85)90002-8.
- ↑ Katehakis, M.N.; Robbins, H. (1995). "Sequential choice from several populations". Proceedings of the National Academy of Sciences of the United States of America. 92 (19): 8584–5. Bibcode:1995PNAS...92.8584K. doi:10.1073/pnas.92.19.8584. PMC 41010. PMID 11607577.
- ↑ Burnetas, A.N.; Katehakis, M.N. (1996). "Optimal adaptive policies for sequential allocation problems". Advances in Applied Mathematics. 17 (2): 122–142. doi:10.1006/aama.1996.0007.
- ↑ Burnetas, A.N.; Katehakis, M.N. (1997). "Optimal adaptive policies for Markov decision processes". Math. Oper. Res. 22 (1): 222–255. doi:10.1287/moor.22.1.222.
- ↑ Tewari, A.; Bartlett, P.L. (2008). "Optimistic linear programming gives logarithmic regret for irreducible MDPs" (PDF). Advances in Neural Information Processing Systems. 20. CiteSeerX 10.1.1.69.5482. Archived from the original (PDF) on 25 May 2012. Retrieved 30 January 2023.
- ↑ Ortner, R. (2010). "Online regret bounds for Markov decision processes with deterministic transitions". Theoretical Computer Science. 411 (29): 2684–2695. doi:10.1016/j.tcs.2010.04.005.
- ↑ Filippi, S. and Cappé, O. and Garivier, A. (2010). "Online regret bounds for Markov decision processes with deterministic transitions", Communication, Control, and Computing (Allerton), 2010 48th Annual Allerton Conference on, pp. 115–122
- ↑ Honda, J.; Takemura, A. (2011). "An asymptotically optimal policy for finite support models in the multi-armed bandit problem". Machine Learning. 85 (3): 361–391. arXiv:0905.2776. doi:10.1007/s10994-011-5257-4.
- ↑ Pilarski, Sebastian; Pilarski, Slawomir; Varró, Dániel (February 2021). "Optimal Policy for Bernoulli Bandits: Computation and Algorithm Gauge". IEEE Transactions on Artificial Intelligence. 2 (1): 2–17. doi:10.1109/TAI.2021.3074122. ISSN 2691-4581.
- ↑ Pilarski, Sebastian; Pilarski, Slawomir; Varro, Daniel (2021). "Delayed Reward Bernoulli Bandits: Optimal Policy and Predictive Meta-Algorithm PARDI". IEEE Transactions on Artificial Intelligence. 3 (2): 152–163. doi:10.1109/TAI.2021.3117743. ISSN 2691-4581.
- ↑ Averbeck, B.B. (2015). "Theory of choice in bandit, information sampling, and foraging tasks". PLOS Computational Biology. 11 (3): e1004164. Bibcode:2015PLSCB..11E4164A. doi:10.1371/journal.pcbi.1004164. PMC 4376795. PMID 25815510.
- ↑ Costa, V.D.; Averbeck, B.B. (2019). "Subcortical Substrates of Explore-Exploit Decisions in Primates". Neuron. 103 (3): 533–535. doi:10.1016/j.neuron.2019.05.017. PMC 6687547. PMID 31196672.
- ↑ Sutton, R. S. & Barto, A. G. 1998 Reinforcement learning: an introduction. Cambridge, MA: MIT Press.
- ↑ Tokic, Michel (2010), "Adaptive ε-greedy exploration in reinforcement learning based on value differences" (PDF), KI 2010: Advances in Artificial Intelligence, Lecture Notes in Computer Science, vol. 6359, Springer-Verlag, pp. 203–210, doi:10.1007/978-3-642-16111-7_23, ISBN 978-3-642-16110-0.
- ↑ Tokic, Michel; Palm, Günther (2011), "Value-Difference Based Exploration: Adaptive Control Between Epsilon-Greedy and Softmax" (PDF), KI 2011: Advances in Artificial Intelligence, Lecture Notes in Computer Science, vol. 7006, Springer-Verlag, pp. 335–346, ISBN 978-3-642-24455-1.
- ↑ Gimelfarb, Michel; Sanner, Scott; Lee, Chi-Guhn (2019), "ε-BMC: A Bayesian Ensemble Approach to Epsilon-Greedy Exploration in Model-Free Reinforcement Learning" (PDF), Proceedings of the Thirty-Fifth Conference on Uncertainty in Artificial Intelligence, AUAI Press, p. 162.
- ↑ Bouneffouf, D.; Bouzeghoub, A.; Gançarski, A. L. (2012), "A Contextual-Bandit Algorithm for Mobile Context-Aware Recommender System", Neural Information Processing, Lecture Notes in Computer Science, vol. 7665, p. 324, doi:10.1007/978-3-642-34487-9_40, ISBN 978-3-642-34486-2
- ↑ Scott, S.L. (2010), "A modern Bayesian look at the multi-armed bandit", Applied Stochastic Models in Business and Industry, 26 (2): 639–658, doi:10.1002/asmb.874
- ↑ Olivier Chapelle; Lihong Li (2011), "An empirical evaluation of Thompson sampling", Advances in Neural Information Processing Systems 24 (NIPS), Curran Associates, 24: 2249–2257
- ↑ Vermorel, Joannes; Mohri, Mehryar (2005), Multi-armed bandit algorithms and empirical evaluation (PDF), In European Conference on Machine Learning, Springer, pp. 437–448
- ↑ Langford, John; Zhang, Tong (2008), "The Epoch-Greedy Algorithm for Contextual Multi-armed Bandits", Advances in Neural Information Processing Systems 20, vol. 20, Curran Associates, Inc., pp. 817–824
- ↑ Lihong Li; Wei Chu; John Langford; Robert E. Schapire (2010), "A contextual-bandit approach to personalized news article recommendation", Proceedings of the 19th International Conference on World Wide Web (WWW 2010): 661–670, arXiv:1003.0146, Bibcode:2010arXiv1003.0146L, doi:10.1145/1772690.1772758, ISBN 9781605587998
- ↑ Wei Chu; Lihong Li; Lev Reyzin; Robert E. Schapire (2011), "Contextual bandits with linear payoff functions" (PDF), Proceedings of the 14th International Conference on Artificial Intelligence and Statistics (AISTATS): 208–214
- ↑ Rigollet, Philippe; Zeevi, Assaf (2010), Nonparametric Bandits with Covariates, Conference on Learning Theory, COLT 2010, arXiv:1003.1630, Bibcode:2010arXiv1003.1630R
- ↑ Slivkins, Aleksandrs (2011), Contextual bandits with similarity information. (PDF), Conference on Learning Theory, COLT 2011
- ↑ Perchet, Vianney; Rigollet, Philippe (2013), "The multi-armed bandit problem with covariates", Annals of Statistics, 41 (2): 693–721, arXiv:1110.6084, doi:10.1214/13-aos1101
- ↑ Sarah Filippi; Olivier Cappé; Aurélien Garivier; Csaba Szepesvári (2010), "Parametric Bandits: The Generalized Linear Case", Advances in Neural Information Processing Systems 23 (NIPS), Curran Associates, 23: 586–594
- ↑ Lihong Li; Yu Lu; Dengyong Zhou (2017), "Provably optimal algorithms for generalized linear contextual bandits", Proceedings of the 34th International Conference on Machine Learning (ICML): 2071–2080, arXiv:1703.00048, Bibcode:2017arXiv170300048L
- ↑ Kwang-Sung Jun; Aniruddha Bhargava; Robert D. Nowak; Rebecca Willett (2017), "Scalable generalized linear bandits: Online computation and hashing", Advances in Neural Information Processing Systems 30 (NIPS), Curran Associates, 30: 99–109, arXiv:1706.00136, Bibcode:2017arXiv170600136J
- ↑ Branislav Kveton; Manzil Zaheer; Csaba Szepesvári; Lihong Li; Mohammad Ghavamzadeh; Craig Boutilier (2020), "Randomized exploration in generalized linear bandits", Proceedings of the 23rd International Conference on Artificial Intelligence and Statistics (AISTATS), arXiv:1906.08947, Bibcode:2019arXiv190608947K
- ↑ Allesiardo, Robin; Féraud, Raphaël; Djallel, Bouneffouf (2014), "A Neural Networks Committee for the Contextual Bandit Problem", Neural Information Processing – 21st International Conference, ICONIP 2014, Malaisia, November 03-06,2014, Proceedings, Lecture Notes in Computer Science, vol. 8834, Springer, pp. 374–381, arXiv:1409.8191, doi:10.1007/978-3-319-12637-1_47, ISBN 978-3-319-12636-4
- ↑ Michal Valko; Nathan Korda; Rémi Munos; Ilias Flaounas; Nello Cristianini (2013), Finite-Time Analysis of Kernelised Contextual Bandits, 29th Conference on Uncertainty in Artificial Intelligence (UAI 2013) and (JFPDA 2013)., arXiv:1309.6869, Bibcode:2013arXiv1309.6869V
- ↑ Féraud, Raphaël; Allesiardo, Robin; Urvoy, Tanguy; Clérot, Fabrice (2016). "Random Forest for the Contextual Bandit Problem". Aistats: 93–101. Archived from the original on 10 August 2016. Retrieved 30 January 2023.
- ↑ Alekh Agarwal; Daniel J. Hsu; Satyen Kale; John Langford; Lihong Li; Robert E. Schapire (2014), "Taming the monster: A fast and simple algorithm for contextual bandits", Proceedings of the 31st International Conference on Machine Learning (ICML): 1638–1646, arXiv:1402.0555, Bibcode:2014arXiv1402.0555A
- ↑ Contextual Bandit with Restricted Context, Djallel Bouneffouf, 2017 <https://www.ijcai.org/Proceedings/2017/0203.pdf>
- ↑ Badanidiyuru, A.; Langford, J.; Slivkins, A. (2014), "Resourceful contextual bandits" (PDF), Proceeding of Conference on Learning Theory (COLT)[پیوند مرده]
- ↑ Wu, Huasen; Srikant, R.; Liu, Xin; Jiang, Chong (2015), "Algorithms with Logarithmic or Sublinear Regret for Constrained Contextual Bandits", The 29th Annual Conference on Neural Information Processing Systems (NIPS), Curran Associates, 28: 433–441, arXiv:1504.06937, Bibcode:2015arXiv150406937W



















