دستگاه اعداد یکانی
| دستگاه شمارش |
|---|
| عددنویسی هندی-عربی |
| آسیای شرقی |
| آمریکایی |
|
| الفبایی |
| پیشینیان |
| ارزش مکانی براساس مبنا |
| دستگاه اعداد مکانی غیر-استاندارد |
| فهرست دستگاه اعداد |
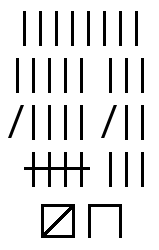
دستگاه اعداد یکانی (به انگلیسی: unary numeral system) سادهترین دستگاه عددی برای نمایش اعداد طبیعی است:[۱] برای نشان دادن یک عدد N، نمادی که ۱ را نشان میدهد N بار تکرار میشود.[۲]
در دستگاه یکانی، عدد ۰ (صفر) با رشته تهی نمایش داده میشود، یعنی عدم وجود نماد. اعداد ۱، ۲، ۳، ۴، ۵، ۶، … به صورت یکانی به صورت ۱، ۱۱، ۱۱۱، ۱۱۱۱، ۱۱۱۱۱، ۱۱۱۱۱۱، … نمایش داده میشوند.[۳]
یکانی یک دستگاه اعداد دوسویی است. با این حال، از آنجایی که مقدار یک رقم به موقعیت آن بستگی ندارد، شکلی از ارزش مکانی نیست، و مشخص نیست که آیا مناسب است بگوییم که پایه (یا «مبنا») آن ۱ است یا خیر. بهطوری که رفتار آن متفاوت از همه پایههای دیگر است.[نیازمند منبع]
استفاده از نشانههای چوبخط در شمارش، کاربرد دستگاه اعداد یکانی است. به عنوان مثال، با استفاده از نشانههای چوپخط | (𝍷)، عدد ۳ به صورت ||| نمایش داده میشود. در فرهنگهای آسیای شرقی، عدد ۳ به صورت 三 نمایش داده میشود، نویسهای که با سه خط کشیده شدهاست.[۴] (یک و دو بهطور مشابه نشان داده شدهاند) در چین و ژاپن، نویسه 正 که با ۵ خط کشیده شدهاست، گاهی برای نشان دادن ۵ به عنوان یک چوبخط استفاده میشود.[۵][۶]
اعداد یکانی باید از یکیتکریها متمایز شوند، که آنها نیز به صورت دنباله ای از یکها نوشته میشوند اما تفسیر عددی اعشاری معمول خود را دارند.
اعمال ریاضی
[ویرایش]جمع و تفریق بهویژه در دستگاه یکانی ساده هستند، زیرا چیزی بیشتر از الحاق رشتهها را شامل میشوند.[۷] عملیات وزن همینگ یا شمارش جمعیت که تعداد بیتهای غیرصفر را در دنبالهای از مقادیر باینری شمارش میکند نیز ممکن است بهعنوان تبدیل از شکل یکانی به اعداد باینری تفسیر شود.[۸] با این حال، ضرب دشوارتر است و اغلب به عنوان نمونه آزمایشی برای طراحی ماشینهای تورینگ استفاده میشود.[۹][۱۰][۱۱]
جستارهای وابسته
[ویرایش]منابع
[ویرایش]- ↑ Hodges, Andrew (2009), One to Nine: The Inner Life of Numbers, Anchor Canada, p. 14, ISBN 978-0-385-67266-5.
- ↑ Davis, Martin; Sigal, Ron; Weyuker, Elaine J. (1994), Computability, Complexity, and Languages: Fundamentals of Theoretical Computer Science, Computer Science and Scientific Computing (2nd ed.), Academic Press, p. 117, ISBN 978-0-12-206382-4.
- ↑ Hext, Jan (1990), Programming Structures: Machines and Programs, Programming Structures, vol. 1, Prentice Hall, p. 33, ISBN 978-0-7248-0940-0.
- ↑ Woodruff, Charles E. (1909), "The Evolution of Modern Numerals from Ancient Tally Marks", American Mathematical Monthly, 16 (8–9): 125–33, doi:10.2307/2970818, JSTOR 2970818.
- ↑ Hsieh, Hui-Kuang (1981), "Chinese Tally Mark", The American Statistician, 35 (3): 174, doi:10.2307/2683999, JSTOR 2683999
- ↑ Lunde, Ken; Miura, Daisuke (January 27, 2016), "Proposal to Encode Five Ideographic Tally Marks", Unicode Consortium (PDF), Proposal L2/16-046
- ↑ Sazonov, Vladimir Yu. (1995), "On feasible numbers", Logic and computational complexity (Indianapolis, IN, 1994), Lecture Notes in Comput. Sci., vol. 960, Springer, Berlin, pp. 30–51, doi:10.1007/3-540-60178-3_78, ISBN 978-3-540-60178-4, MR 1449655. See in particular p. 48.
- ↑ Blaxell, David (1978), "Record linkage by bit pattern matching", in Hogben, David; Fife, Dennis W. (eds.), Computer Science and Statistics--Tenth Annual Symposium on the Interface, NBS Special Publication, vol. 503, U.S. Department of Commerce / National Bureau of Standards, pp. 146–156.
- ↑ Hopcroft, John E.; Ullman, Jeffrey D. (1979), Introduction to Automata Theory, Languages, and Computation, Addison Wesley, Example 7.7, pp. 158–159, ISBN 978-0-201-02988-8.
- ↑ Dewdney, A. K. (1989), The New Turing Omnibus: Sixty-Six Excursions in Computer Science, Computer Science Press, p. 209, ISBN 978-0-8050-7166-5.
- ↑ Rendell, Paul (2015), "5.3 Larger Example TM: Unary Multiplication", Turing Machine Universality of the Game of Life, Emergence, Complexity and Computation, vol. 18, Springer, pp. 83–86, ISBN 978-3-319-19842-2.
