خودهمبستگی اپتیکی

طبقه بندی انواع روش های خود همبستگی نوری.

در اپتیک ، توابع خودهمبستگی مختلف را می توان تجربه کرد. برای محاسبه طیف منبع نور، می توان از خودهمبستگی میدان استفاده کرد ، در حالی که همبستگی شدت و همبستگی تداخلی معمولاً برای برآورد طول پالس های فوق تولید شده توسط لیزر های مد لاک استفاده می شود . طول پالس لیزر را نمی توان با روش های الکترونیکی اندازه گیری کرد، زیرا زمان پاسخ فوتو دیودها و اسیلوسکوپ در بهترین حالت از 200 فمتوثانیه است ، در حالی که پالس های لیزری را می توان تا چند فمتوثانیه کوتاه ساخت.

در مثال های زیر، سیگنال اتخاذ خودکار توسط فرایند غیرخطی هارمونیک دوم (SHG) تولید می شود. روش های دیگر مبتنی بر جذب دو فوتون و نیز فرایندهای نوری غیر خطی مرتبه بالاتر مانند هارمونیک سوم ، می توانند در اندازه گیری خود همبستگی استفاده شوند ، در این صورت معادلات ریاضی سیگنال کمی اصلاح خواهند شد، اما نتایج یکسان است . در مورد خود همبستگی تداخلی در چندین کتاب بحث و بررسی شده است..

خود همبستگی میدانی

راه اندازی برای خودهمبستگی میدان، بر اساس یک تداخل سنج مایکلسون . L : لیزر مد لاک ، BS : بیم اسپیلیتر ، M1 : آینه متحرک یک تاخیر فاز متغیر ایجاد می کند ، M2 : آینه ثابت، D : آشکارساز نور.

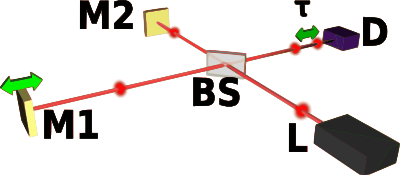
برای میدان الکتریکی $E(t)$ تابع خودهمبستگی چنین تعریف شده :

$E(t)$

$E(t)$$A(\tau )=\int _{-\infty }^{+\infty }E(t)E^{*}(t-\tau )dt$

قضیه Wiener-Khinchin بیان کند که تبدیل فوریه خودهمبستگی میدانی همان طیف است. در نتیجه، خودهمبستگی میدان به فاز طیفی حساس نیست.

با استفاده از یک آشکارساز کند در خروجی یک تداخل سنجی مایکلسون، خود همبستگی میدان به راحتی اندازه گیری می شود. آشکارساز توسط میدان الکتریکی ورودی $E(t)$ از یکی از بازو ها و توسط $E(t-\tau )$ از بازوی دیگر روشن می شود . اگر پاسخ زمان آشکارساز بسیار بزرگتر از مدت زمان سیگنال $E(t)$ باشد ، و یا اگر سیگنال ثبت شده یکپارچه شود، آشکارساز شدت $I_{M}$ که به اندازه ی $\tau$$\tau$$\tau$ تاخیر دارد را اندازه گیری می کند $I_{M}$ :

$I_{M}(\tau )=\int _{-\infty }^{+\infty }|E(t)+E(t-\tau )|^{2}dt$

بسط $I_{M}(\tau )$ نشان می دهد که یکی از پارامترها $A(\tau )$ است این را بیان می کند که یک تداخل سنجی مایکلسون می تواند برای اندازه گیری خود همبستگی میدان یا طیف $E(t)$ (و تنها طیف) استفاده شود. این اصل مبنایی برای طیف سنجی تبدیل فوریه است.

دو پالس فوق العاده کوتاه (a) و (b) با همبستگی خودکار (c) و (d) مربوطه. توجه داشته باشید که خودهمبستگی متقارن هستند و در صفر تاخیر صفر هستند. همچنین توجه داشته باشید که بر خلاف پالس (a)، پالس (b) یک فرکانس فوری را نشان می دهد که فشرده شده است ،که چرپ شدن نام دارد و بنابراین دارای پهنای باند بیشتری نسبت به پالس (a) دارد. بنابراین، خودهمبستگی میدان (d) کوتاهتر از (c) است، زیرا طیف، تبدیل فوریه خودهمبستگی میدان است (قضیه وینر-کینچین).

خودهمبستگی شدت

میدان الکتریکی پیچیده $E(t)$ به شدت مطابقت دارد $I(t)=|E(t)|^{2}$ $I(t)=|E(t)|^{2}$ $I(t)=|E(t)|^{2}$ و یک تابع خودهمبستگی شدت تعریف شده

$A(\tau )=\int _{-\infty }^{+\infty }I(t)I(t-\tau )dt$$A(\tau )=\int _{-\infty }^{+\infty }I(t)I(t-\tau )dt$

$A(\tau )=\int _{-\infty }^{+\infty }I(t)I(t-\tau )dt$

پیاده سازی اپتیک خود همبستگی شدت به همان نسبت برای خود همبستگی میدان ساده نیست. به طور مشابه با تنظیم قبلی، دو پرتو موازی با تاخیر متغیر تولید می شوند سپس برای برای دریافت سیگنال متناسب با$(E(t)+E(t-\tau ))^{2}$ به یک کریستال هارمونیک دوم متمرکز می شوند . فقط پرتو یی که در محور نوری منتشر می شود عبارت متناسب با $E(t)E(t-\tau )$ تولید می کند. این سیگنال توسط یک آشکارساز آهسته اندازه گیری می شود

$I_{M}(\tau )=\int _{-\infty }^{+\infty }|E(t)E(t-\tau )|^{2}dt=\int _{-\infty }^{+\infty }I(t)I(t-\tau )dt$

شکست در تجزیه (خطای نحوی): {\displaystyle <mrow class="MJX-TeXAtom-ORD"><mstyle displaystyle="true" scriptlevel="0"><msub><mi> <math>I_M(\tau)} </mi><mrow class="MJX-TeXAtom-ORD"><mi> $I_{M}(\tau )$ </mi></mrow></msub><mo stretchy="false"> $I_{M}(\tau )$ </mo><mi> $I_{M}(\tau )$ </mi><mo stretchy="false"> $I_{M}(\tau )$ </mo></mstyle></mrow> </math>$I_{M}(\tau )$ دقیقاً خود همبستگی شدت $A(\tau )$ است .

تولید هارمونیک دوم در بلورها یک فرایند غیرخطی است که نیاز به توان پیک بالایی دارد. با این وجود، این پیک بسیار قدرت بالا می تواند از یک مقدار محدود انرژی توسط پالس های قوق کوتاه گرفته شود و به همین دلیل خود همبستگی شدت آنها اغلب به صورت آزمایشی اندازه گیری می شود. مشکل دیگر این است که هر دو پرتو باید در یک نقطه در داخل کریستال متمرکز شوند.

می توان نشان داد که خود همبستگی شدت یک پالس با طول پالس رابطه دارد. اگر مشخصات پالس گوسی باشد ، عرض خودهمبستگی ${\sqrt {2}}$ طولانی تر از عرض شدت پالس است. برای فرض با پالس مربع هذلولی (sech ² ) این عدد 1.54 است . این عامل عددی، که به شکل پالس بستگی دارد، بعدها فاکتور deconvolution نامیده می شود . اگر این فاکتور تعیین شده یا فرض شود، مدت زمان طول یک پالس را می توان با استفاده از خود همبستگی شدت اندازه گیری کرد. با این حال، فاز را نمی توان اندازه گیری کرد.

دو پالس فوق العاده کوتاه (a) و (b) با وابستگی شدت خود (c) و (d). از آنجائیکه همخوانی خودکار شدت، فاز زمانی پالس (b) را که به علت فرکانس جاری ( chirp ) است، نادیده گرفته می شود، هر دو پالس همان خود همبستگی شدت را با هم مقایسه می کنند. در اینجا، پروفیل های زمانی گاوسی یکسان استفاده شده است، که موجب شدت ارتعاشات شدت ^1/2 2 بیشتر از شدت های اصلی است. توجه داشته باشید که ارتباط خودکار شدت دارای زمینه ای است که به طور ایده‌آل نیمی از اندازه سیگنال واقعی است. صفر این رقم تغییر یافته است تا این پس زمینه را حذف کند.

خود همبستگی تداخلی

تنظیم برای یک اتوکپلرتر تداخلی، شبیه به autocorrelator میدان در بالا، با لنز نیز اضافه شده است: L : لنز همگرا ، SHG : کریستال هارمونیک دوم ، F : فیلتر رنگی برای جلوگیری از ورود طول موج بنیادی.

به عنوان ترکیبی از هر دو مورد قبلی، یک کریستال غیر خطی می تواند برای تولید هارمونیک دوم در خروجی یک تداخل سنجی ماکلسون استفاده شود . در این مورد، سیگنال ثبت شده توسط آشکارساز آهسته به صورت زیر است:

$I_{M}(\tau )=\int _{-\infty }^{+\infty }|(E(t)+E(t-\tau ))^{2}|^{2}dt$

شکست در تجزیه (خطای نحوی): {\displaystyle <mrow class="MJX-TeXAtom-ORD"><mstyle displaystyle="true" scriptlevel="0"><msub><mi> <math>I_M(\tau)} </mi><mrow class="MJX-TeXAtom-ORD"><mi> $I_{M}(\tau )$ </mi></mrow></msub><mo stretchy="false"> $I_{M}(\tau )$ </mo><mi> $I_{M}(\tau )$ </mi><mo stretchy="false"> $I_{M}(\tau )$ </mo></mstyle></mrow> </math>$I_{M}(\tau )$ خودهمبستگی تداخلی نامیده می شود. این پارامتر حاوی اطلاعاتی در مورد فاز پالس است.

دو پالس فوق کوتاه (a) و (b) با خود همبستگی تداخلی (c) و (d) بین دو سنجنده . به علت فاز موجود در پالس (b) به علت فرکانس بارگیری سریع ( چرپ )، حاشیه ردیابی (autocorrelation (d در بال ها شسته شده است. توجه نسبت 1 : 8 (پیک به بال ها)، مشخصه اثرات اتخاذ تصادفی interferometric.

خودهمبستگی تابع مردمک

تابع انتقال اپتیکی( T(w یک سیستم اپتیکی از خودهمبستگی( f(x,y تابع مردمک آن سیستم بدست می آید:

$T(w)={\frac {\int _{w/2}^{1}\int _{0}^{\sqrt {1-x^{2}}}f(x,y)f^{*}(x-w,y)dydx}{\int _{0}^{1}\int _{0}^{\sqrt {1-x^{2}}}f(x,y)^{2}dydx}}$

همچنین نگاه کنید

• اتوکریلاتور
• کانولوشن
• فاز تداخل داخل پالسی چند فتونی اسکن
• تداخل سنجی فاز طیفی برای بازسازی مستقیم برق میدان