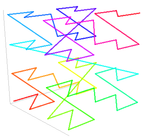
خم مرتبه زد

چهار تکرار از منحنی مرتبه Z.

تکرارهای منحنی مرتبه Z در سه بعد تعمیم داده شده‌است.

در آنالیز ریاضی و علوم رایانه، توابع ای مانند مرتبه Z، منحنی Lebesgue، منحنی پر کردن فضای مورتون، مرتبه مورتون یا کد مورتون داده‌های چند بعدی را در یک بعد حفظ کرده و در عین حال محلی از نقاط داده را حفظ می‌کنند. این نام از گای مک دونالد مورتون گرفته شده‌است که برای اولین بار دستور ترتیب دهی فایل‌ها را در سال ۱۹۶۶ داد. مقدار z یک نقطه در چند بعد به سادگی با در هم آمیختن مقادیر دودویی مختصات آن محاسبه می‌شود. پس از طبقه‌بندی داده‌ها به این ترتیب، می‌توان از هر داده ساختار یک بعدی مانند درخت جستجوی دودویی، درختان B، لیست پرشی یا جدول‌های درهمسازی استفاده کرد. ترتیب حاصل معادل ترتیب بدست آمده از عمق اول یک چاردرخت توصیف می‌شود.

مقادیر مختصات

جدول زیر مقادیر Z را در دو بعد نشان می‌دهد که ۰ ≤ x ≤ ۷، ۰ ≤ y ≤ ۷ است (هم در مبنای ۱۰ و هم به صورت دودویی نشان داده می‌شود) در هم آمیختن مقادیر مختصات باینری مقادیر باینری z را بازمی‌گرداند. متصل کردن مقادیر z به ترتیب عددی آن‌ها یک خم بازگشتی Z شکل را می‌سازد.

مقادیر Z از xها به عنوان اعداد باینری از دنبالهٔ Moser–de Bruijn در نظر گرفته می‌شوند و فقط در موقعیت‌های مساوی خود دارای بیت‌های غیرصفر هستند:

 {x[] = {0b000000, 0b000001, 0b000100, 0b000101, 0b010000, 0b010001, 0b010100, 0b010101

مجموع و تفاوت دو x با استفاده از عملیات بیتی محاسبه می‌شود:

 x[i+j] = ((x[i] | 0b10101010) + x[j]) & 0b01010101
 (x[i-j] = (x[i] & 0b01010101) - x[j]) & 0b01010101 if i>= j

از این ویژگی می‌توان برای متعادل کردن مقدار Z استفاده کرد، برای مثال در دو بعد مختصات رو به بالا (کاهش y)، پایین (افزایش y)، سمت چپ (کاهش x) و سمت راست (افزایش x) از مقدار Z فعلی برابر است با:

 (top    = ((z & 0b10101010) - 1 & 0b10101010) | (z & 0b01010101
 (bottom = ((z | 0b01010101) + 1 & 0b10101010) | (z & 0b01010101
 (left   = ((z & 0b01010101) - 1 & 0b01010101) | (z & 0b10101010
 (right  = ((z | 0b10101010) + 1 & 0b01010101) | (z & 0b10101010

و به‌طور کلی برای اضافه کردن دو مقدار Z دو بعدی:

 (sum = ((z | 0b10101010) + (w & 0b01010101) & 0b01010101) | ((z | 0b01010101) + (w & 0b10101010) & 0b10101010

ساختن چهاردرخت به‌طور مؤثر

از مرتب‌سازی Z می‌توان برای ساختن یک چاردرخت برای مجموعه‌ای از نقاط استفاده کرد. ایدهٔ اصلی این است که مجموعهٔ ورودی را مطابق مرتبه Z مرتب کنید. پس از مرتب‌سازی، نقاط هم می‌توانند در یک درخت دودویی جستجوی ذخیره شوند و به‌طور مستقیم استفاده شوند، که به آن چاردرخت خطی گفته می‌شود، و هم می‌توانند برای ساخت یک چاردرخت مبتنی بر پوینتر استفاده شوند.

نقاط ورودی معمولاً در هر بعدی به صورت اعداد صحیح مثبت هستند، چه به عنوان یک نقطه ثابت در محدوده [۰ ، ۱] و چه متناسب با طول کلمه دستگاه. هر دو نمایش معادل هستند و اجازه می‌دهند بالاترین مرتبه بیت غیر صفر در زمان ثابت یافت شود. هر مربع در چاردرخت دارای طول ضلع است که توان آن دو است و مختصات گوشه که مضرب طول ضلع است. با توجه به هر دو نقطه، مربع بدست آمده برای دو نقطه، کوچکترین مربع است که هر دو نقطه را پوشش می‌دهد. به مخلوط کردن بیت‌های مؤلفه‌های x و y هر نقطه، شافل (shuffle) نقاط x و y گفته می‌شود و می‌تواند برای ابعاد بالاتر هم تعمیم پیدا کند.

نقاط را می‌توان با توجه به شافل آن‌ها طبقه‌بندی کرد بدون اینکه صریحاً بیت‌ها در هم آمیخته شود. برای انجام این کار، برای هر بعد، چپ‌ترین بیت از XOR مختصات دو نقطه، برای آن بعد مورد بررسی قرار می‌گیرد. بعدی که بیت سمت چپ آن از بقیه بزرگتر است برای مقایسه دو نقطه برای تعیین ترتیب شافل آن‌ها استفاده می‌شود.

عملیات XOR بیت‌های مرتبه بالاتر که در آن‌ها دو مختصات یکسان هستند را تعیین می‌کند. از آنجا که شافل، بیت‌ها را از مرتبه بالاتر به مرتبه پایین‌تر به هم می‌ریزد، مختصات با بزرگترین بیت سمت چپ را اینگونه شناسایی می‌کند که ابتدا اولین بیت در ترتیب شافل که متفاوت است را شناسایی می‌کند و از این مختصات برای مقایسه دو نقطه استفاده می‌کند. کد پایتون این عملیات به صورت زیر است:

    def cmp_zorder(lhs, rhs):
        # assume lhs and rhs array-like objects of indices
        assert len(lhs) == len(rhs)
        # will contain the most significant dimension
        msd = 0
        # loop over the other dimensions
        for dim in range(1, len(lhs)):
            # check if the current dimension is more significant
            # by comparing the most significant bits
            if less_msb(lhs[msd] ^ rhs[msd], lhs[dim] ^ rhs[dim]):
                msd = dim
        return lhs[msd] <rhs[msd]

یک راه برای تعیین اینکه آیا بیت سمت چپ کوچکتر است، مقایسه کف لگاریتم پایه-۲ هر نقطه است. عملیات زیر معادل است و فقط به عملیات xor نیاز دارد:

    def less_msb(x, y):
        return x <y and x <(x ^ y)

همچنین می‌توان اعداد ممیز شناور را با استفاده از همین تکنیک مقایسه کرد. تابع less_msb ابتدا اکسپوننت‌ها (قسمت توان اعداد شناور) را مقایسه می‌کند. فقط وقتی مساوی باشند، تابع less_msb روی مانتیساها (قسمت عدد اعداد شناور) اعمال می‌شود.

هنگامی که امتیازها مرتب شدند، دو ویژگی باعث می‌شود که یک چاردرخت آسان ساخته شود: اولین نکته این است که نقاط موجود در یک مربع چاردرخت، به صورت مرتب شده و با فاصلهٔ متناوب باشند. دوم اینکه اگر بیش از یک بچهٔ مربع دارای یک نقطه ورودی باشد، مربع از دو نقطهٔ مرتب شدهٔ مجاور نشات گرفته شده‌است.

برای هر دو نقطهٔ مجاور، مربع بدست آمده محاسبه می‌شود و طول آن مشخص می‌شود و برای هر مربع بدست آمده، فاصلهٔ شامل آن مربع توسط اولین مربع بزرگتر سمت راست و اولین مربع بزرگتر سمت چپ که به صورت مرتب شده هستند بدست می‌آید. هر کدام از این فاصله‌ها با مربع چاردرخت مطابقت دارد. نتیجه این کار یک چاردرخت فشرده شده‌است، که در آن فقط گره‌های حاوی نقاط ورودی یا دو یا چند بچه در آن حضور دارند. در صورت تمایل می‌توانید با قرار دادن گره‌های از دست رفته یک چاردرخت غیر فشرده بسازید.

به جای ایجاد یک چاردرخت مبتنی بر پوینتر، نقاط را می‌توان به صورت مرتب شده در داده ساختاری مانند درخت جستجوی دودویی حفظ کرد. این کار به ما اجازه می‌دهد تا در زمان (O(log n نقاط را درج و حذف کنیم. دو چاردرخت را می‌توان با ادغام دو مجموعهٔ مرتب شده از نقاط، و از بین بردن تکراری‌ها ادغام کرد. جای نقاط را می‌توان با جستجوی نقاط قبل و دنبال کردن نقطهٔ پرسیده شده به ترتیب مرتب شده انجام داد. اگر چاردرخت فشرده شده باشد، گره قبلی پیدا شده ممکن است یک برگ دلخواه در داخل گره فشرده شدهٔ مورد نظر باشد. در این حالت، لازم است که اولین جد مشترک نقطه پرسیده شده و برگ پیدا شده را پیدا کنیم.

استفاده برای جستجوی دامنه با داده ساختارهای یک بعدی

اگرچه این کار به خوبی مکان را حفظ می‌کند ولی برای جستجوی کارآمد دامنه، یک الگوریتم برای محاسبات از نقطه‌ای که در داده ساختار مشاهده می‌شود تا مقدار بعدی Z که در محدوده جستجو چند بعدی است لازم است:

در این مثال، دامنه درخواست شده (x = ۲، … , 3, y = ۲، … , ۶) توسط خط چین مستطیل شکل نشان داده شده‌است. بزرگترین مقدار Z آن ۴۵ است. در این مثال مقدار F = ۱۹ در هنگام جستجوی یک داده ساختار در جهت افزایش مقدار Z با مشکل روبرو می‌شود، بنابراین باید در فاصلهٔ بین F و مقدار بیشینه جستجو کنیم. برای سرعت بخشیدن به جستجو، مقدار بعدی Z را که در محدوده جستجو قرار دارد محاسبه می‌کنیم که به آن مینیمم بزرگ می‌گوییم (نقطهٔ ۳۶ در مثال) و فقط در بازهٔ بین مینیمم بزرگ و نقطهٔ بیشینه جستجو می‌کنیم، بنابراین از بسیاری از قسمت‌ها می‌پریم. جستجو در جهت کاهش مقدار، مشابه با LITMAX است که همان بیشترین مقدار Z در دامنهٔ پرسیده شدهٔ کوچک‌تر از F است. ابتدا مسئله BIGMIN بیان شده‌است و راه حل آن در Tropf و Herzog نشان داده شده‌است. این راه حل همچنین در درختان UB استفاده می‌شود. از آنجا که این رویکرد به داده ساختار یک بعدی انتخاب شده بستگی ندارد، انتخاب داده ساختار هنوز آزاد است، بنابراین می‌توان از روش‌های شناخته شده‌ای مانند درختان متوازن استفاده کرد (در مقابل برای داده ساختاری مانند درخت مستطیلی ملاحظات ویژه لازم است) به همین ترتیب، این استقلال باعث می‌شود که قرار دادن این روش در پایگاه داده‌های موجود آسان شود.

استفاده از روش سلسله مراتب (با توجه به داده ساختار موجود)، به صورت اختیاری در هر دو جهت افزایش و کاهش، در بازه چندبعدی بازده بسیار کارآمدی دارد که در هر دو زمینهٔ تجاری و برنامه‌های فنی مهم است، به عنوان مثال روشی برای جستجوی نزدیک‌ترین همسایه. مرتبه Z یکی از معدود روشهای دسترسی چند بعدی است که راه خود را به سیستم‌های پایگاه دادهٔ تجاری پیدا کرده‌است (پایگاه داده اوراکل ۱۹۹۵، ترنسبیس 2000).

در سال ۱۹۶۶، مورتن مرتبه Z را برای ترتیب دهی فایل‌های یک پایگاه داده جغرافیایی ایستا در دو بعد ارائه داد. ناحیهٔ واحدهای داده در یک یا چند فریم چهار درجه‌ای قرار داده شده‌اند که با اندازه‌های خود و گوشهٔ پایین سمت راست مقدار Z خود نشان داده شده‌اند، اندازه‌ها با سلسله مراتب مرتبه Z گوشه‌ها مطابقت دارد. با احتمال زیاد، تغییر به قاب مجاور با یک یا چند مرحله نسبتاً کوچک انجام می‌شود.

ساختارهای مرتبط

به عنوان یک گزینه جایگزین، منحنی هیلبرت پیشنهاد شده‌است زیرا مرتبه را بهتر حفظ می‌کند و در هندسه S2 نیز استفاده شده‌است. قبل از S2، از این روش استفاده نمی‌شد زیرا محاسبات آن پیچیده‌است و منجر به پردازنده‌ای خاص می‌شود.

برای مطالعه راجع‌به پردازش داده‌های چند بعدی مانند جستجوی نزدیکترین همسایه، به کتاب هانان سامت مراجعه کنید.

برنامه‌ها

جدول اضافی برای $x+2y$ جایی که $x$ و $y$ هر دو متعلق به دنبالهٔ Moser – de Bruijn هستند و منحنی مرتبه ی-Z که جمع‌ها را به ترتیب عددی به هم وصل می‌کند

جبر خطی

الگوریتم استراسن برای ضرب ماتریس، مبتنی بر تقسیم ماتریس‌ها به چهار قسمت است و سپس به صورت بازگشتی هر کدام از این قسمت‌ها را نیز به چهار قسمت کوچکتر تقسیم می‌کنیم، تا زمانی که هر قسمت شامل تنها یک عدد باشد (یا به صورت عملی تر: تا وقتی که به ماتریس‌هایی برسیم که اندازه‌های آن به صورتی است که الگوریتم Moser–de Bruijn سریع تر عمل کند). مرتب کردن عناصر ماتریس در مرتبهٔ Z باعث بهبود مکان می‌شود و این مزیت را هم دارد که (در مقایسه با مرتب‌سازی ردیف یا ستون اصلی) که برای ضرب دو قسمت نیازی به دانستن اندازه کل ماتریس نداریم بلکه فقط اندازه قسمت‌ها و مکان آنها در حافظه برای ما کافی است. استفاده مؤثر از ضرب استراسن با مرتبه Z نشان داده شده‌است.

داده ساختار ماتریس خلوت ارائه شده‌است که مرتبه Z روی عناصر غیر صفر آن اعمال می‌شود تا الگوریتم موازی را روی ضرب ماتریس-بردار ممکن سازد.

نگاشت بافت

برخی از واحدهای پردازش گرافیکی نقشه‌های بافت را در مرتبهٔ Z ذخیره می‌کنند تا مکان مرجع را در حین نقشه‌برداری بافت افزایش دهد. این به حافظهٔ نهان سی‌پی‌یو اجازه می‌دهد کاشی‌های مربع را نمایان کند و احتمال این که دسترسی‌های مجاور در حافظه باشند را افزایش می‌دهد. این امری مهم است زیرا رندر کردن سه‌بعدی شامل تغییرات دلخواه (چرخش، مقیاس بندی، چشم‌انداز و تحریف توسط سطوح متحرک) می‌شوند. به اینها بافت‌های سویزلد (swizzled) یا بافت‌های توایدلد (twidled) گفته می‌شوند. همچنین ممکن است از انواع دیگری از کاشی‌ها استفاده شود.

رمزگذاری تصویر/ویدئو

یک تصویر یا یک ویدیو در واقع یک ماتریس است، ماتریس را به برداری از پیکسل‌ها در مرتبهٔ z تبدیل می‌کند، سپس بردار پیکسل را فشرده و رمزگذاری می‌کند.

جستارهای وابسته

• منحنی پر شدن فضا
• درخت UB
• منحنی هیلبرت
• درخت هیلبرت R
• پایگاه داده مکانی
• جوهاش
• محل مرجع
• محل حفظ درهمسازی
• بازنمایی ماتریس
• جبر خطی

پیوند به بیرون

• STANN: کتابخانه‌ای برای جستجوی تقریبی نزدیکترین همسایه ، با استفاده از منحنی مرتبه Z
• روش‌های برنامه‌نویسی کمی interleaving، شان ارون اندرسون، دانشگاه استنفورد