جستجوی درختی

جستجوی درختی از جمله پرکاربردترین استفاده از یک درخت است. درخت یک مدل مناسب برای نمایش بسیاری از مفاهیم، پدیده‌ها و رابطهٔ بین آن‌هاست. مثلاً درخت فامیلی، سلسله مراتب اداری، عبارات ریاضی و بسیاری از بازی‌ها با درخت مدل می‌شوند. در واقع درخت‌ها، گراف‌های خاصی هستند که در مورد ویژگی‌های آن‌ها نتایج نظری زیادی وجود دارد.^[۱]

درخت‌ها بسته به نوع نیاز، تعداد برگ‌های مختلفی دارند. الگوریتم جستجو مختص به تعداد برگ‌های درخت می‌باشد که عبارتند از:درخت جستجوی سه‌تایی ،درخت جستجوی دودویی خود-متوازن ،درخت جستجوی دودویی متوازن وزن‌دار ،درخت جستجوی تعمیم‌یافته، درخت جستجو بندانگشتی و... در اینجا سه نوع جستجوی رایج را در درخت دودویی و درخت با تعداد برگ نامشخص و ترای (همان درخت پیشوندی است که برای جستجوی رشته‌ای مناسب است) بررسی می‌کنیم.

درخت دودویی جستجو

درخت دودویی درخت مرتبی است که هر عنصر آن حداکثر دارای دو فرزند چپ و راست باشد. اگر یک گره فقط یک فرزند داشته باشد، باید مشخص شود که فرزند چپ است یا راست. درخت عبارت و درخت تصمیم نمونه‌هایی از کاربردهای درخت دودویی هستند.^[۱]

معروف به د.د. ج می‌باشد. معمولاً عملیات زیر بر روی یک درخت جستجوی دودویی تعریف می‌شود:

ایجاد یک درخت جستجوی خالی
آزمایش خالی بودن درخت
درج کردن یک کلید جدید در درخت، بدون برهم‌خوردن خاصیت درخت
جستجو کردن و یافتن یک کلید خاص در درخت
حذف کردن یک کلید از درخت، با حفظ خاصیت درخت
پیمایش درخت جستجوی دودویی، به طوری تمام گره‌ها دقیقاً یک بار مورد دسترسی قرارگیرند.

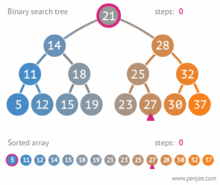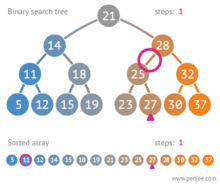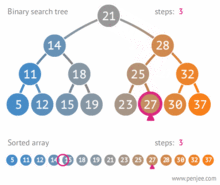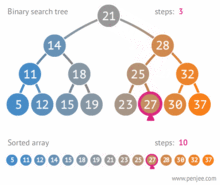
برای پیدا کردن گرهی با یک کلید خاص مانند key در درخت، ابتدا باید از ریشه درخت شروع کنیم. اگر ریشه تهی باشد، درخت فاقد هر عنصری بوده و جستجو ناموفق خواهد بود. در غیر اینصورت، key را با مقدار گره ریشه مقایسه می‌کنیم، اگر برابر بودند، جستجو موفق است و گره ریشه همان گره موردنظر است. در غیر این صورت، دو حالت پیش خواهدآمد:

key از گره ریشه کوچکتر است. در این‌حالت، هیچ عنصری در زیردرخت سمت راست وجود ندارد که مقدار کلید آن برابر با key باشد؛ بنابراین جستجو باید در زیردرخت سمت چپ ادامه‌یابد.
key بزرگتر از گره ریشه است. در این حالت، هیچ عنصری در زیردرخت سمت چپ وجود ندارد که مقدار کلید آن برابر با key باشد؛ بنابراین جستجو باید در زیردرخت سمت راست ادامه‌یابد.

سپس بسته به حالت یک و دو، زیردرخت سمت چپ یا زیردرخت سمت راست را به روش بازگشتی و با استفاده از الگوریتم بالا جستجو می‌کنیم. عمل جستجو در درخت جستجوی دودویی، از مرتبه $O(h)$ است که در آن h ارتفاع درخت است. چرا که حداکثر باید به میزان عمق درخت، به طرف پایین حرکت کنیم. در این الگوریتم،^[۲] هر راس ۳ اشاره‌گر دارد:

اشاره‌گر به پدر
درخت دودویی جستجو
اشاره‌گر به فرزند چپ
اشاره‌گر به فرزند راست

class TreeNode:
    def __init__(self, label):
       
        self.left_child = None
        self.right_child = None
        self.label = label
        self.parent = None

def search_in_BST(node, key):
    if node is None or node.label == key:
        return node
    if node.label < key:
        return search_in_BST(node.leftChild, key)
    else:
        return search_in_BST(node.rightChild, key)

جستجو در درخت با تعداد برگ نامشخص

ممکن است الگوریتمی نیاز داشته‌باشیم که در آن تعداد فرزندان هر راس نامشخص باشد. در اینصورت به درختی نیاز داریم که در آن فرزندان هر راس رابه تعداد دلخواه بتوان‌افزود. در این الگوریتم^[۱]

، هر راس ۳ اشاره‌گر دارد:

اشاره‌گر به پدر
اشاره‌گر به فرزند چپ
اشاره‌گر به راس بعدی در سمت راست خود راس

و برای جستجو، ابتدا برچسب خود راس را چک می‌کنیم اگر برابر با key نبود، برچسب فرزند چپ آن را بررسی می‌کنیم و اگر برابر نبود به سراغ رئوس سمت راست فرزند چپ می‌رویم و تا جایی که به مقدار None نرسیدیم، کار را ادامه می‌دهیم و الگوریتم را به صورت بازگشتی ادامه می‌دهیم. به دلیل اینکه حداکثر همه رئوس برای یکبار جستجو طی می‌شوند، الگوریتم از مرتبه $O(n)$ می‌باشد.

class TreeNode:
    def __init__(self, label):
        self.label = label
        self.parent = None
        self.left_child = None
        self.right_sibling = None
       
       

def find_in_subtree(tree, key, node):
    if node.label == key:
        return node

    child = node.left_child
    while child is not None:
        result = tree.find_in_subtree(key, child)
        if result is not None:
            return result
        child = child.right_sibling

    return None

جستجو در درخت پیشوندی

در علم رایانه ترای یا درخت پیشوندی یک داده ساختار درختی است که برای آرایه‌های شرکت پذیری استفاده می‌شود که کلیدهای آن معمولاً رشته می‌باشند. برخلاف یک درخت دودویی جستجو در این درخت هیچ گرهی، کلیدی را که توسط آن گره مشخص می‌شود ذخیره نمی‌کند؛ در عوض، موقعیت آن در درخت نشان‌دهنده کلید مربوط به آن است. تمام فرزندان یک گره پیشوند مشترکی دارند که این پیشوند در گره مربوطه ذخیره می‌شود. گره ریشه نیز یک رشته خالی است. معمولاً همه گره‌ها مشخص‌کننده کلیدها نیستند. فقط برگ‌ها و بعضی از گره‌های داخلی با کلیدها مرتبط می‌شوند. گره‌های حاوی کلید به نحوی علامت‌گذاری می‌شوند تا تمام کلیدها مشخص شوند. البته یک ترای الزاماً شامل رشته‌های کاراکتری نمی‌باشد، بلکه حتی برای جایگشت‌های عددی و مواردی از این قبیل هم می‌توان از ترای استفاده کرد و از آن در جستجوی لغت نامه‌ها نیز استفاده می‌شود.^[۳]

برای جستجوی رشته یا عبارت در ترای، از ریشه درخت شروع به مقایسه می‌کنیم. در این الگوریتم، یال‌های درخت برچسب دارند و اگر یال ابتدایی برابر با مقدار ابتدای رشته باشد، سایر یال‌های متصل به یال اولیه را بررسی می‌کنیم و به صورت بازگشتی ادامه می‌دهیم تا به انتهای یک رشته که با mark مشخص شده، برسیم.

class Node:
    def __init__(self):
        self.mark = False
        self.edges = []
       
class Edge:
    def __init__(self, start, end, label):
        self.start = start
        self.end = end
        self.label = label

class Trie:
   
    def __init__(self):
        self.root = Node()
       
   
    def find(self, string):
        return trie_find(self.root, string, 0)

اگر تنها جستجوی کل عبارت مدنظر باشد، داریم:

def trie_find(node, string, idx = 0):
        if idx == len(string):
            return node.mark
        found = False
        for edge in node.edges:
            if edge.label == string[idx]:
                found = True
                return trie_find(edge.end, string, idx + 1)
        if not found:
            return False

اگر پیشوندهای عبارت، مدنظر باشد، داریم:

def trie_insert_mark_all(node, string, idx):     
    node.mark = True
    if idx == len(string):
        return
    found = False
    for edge in node.edges:
        if edge.label == string[idx]:
            found = True
            trie_insert_mark_all(edge.end, string, idx + 1) # increasing idx to proceed to the next character
    if not found:
        new_node = Node()
        node.edges.append(Edge(node, new_node, string[idx]))
        trie_insert_mark_all(new_node, string, idx + 1) # increasing idx to proceed to the next character

منابع

↑ ^۱٫۰ ^۱٫۱ ^۱٫۲ قدسی، محمد (۱۳۸۸)، داده ساختارها و مبانی الگوریتم‌ها، تهران: انتشارات فاطمی
↑ Times Roman and Mathtime Pro 2 by the authors (۲۰۰۹)، Introduction to Algorythms، Amherst: Massachusetts Institute of Technonology
↑ "The Trie Data Structure".

[ghodsi-1] ۱٫۰ ^۱٫۱ ^۱٫۲ قدسی، محمد (۱۳۸۸)، داده ساختارها و مبانی الگوریتم‌ها، تهران: انتشارات فاطمی

[clrs-2] Times Roman and Mathtime Pro 2 by the authors (۲۰۰۹)، Introduction to Algorythms، Amherst: Massachusetts Institute of Technonology

[3] "The Trie Data Structure".

[۱]

[۲]

[۳]