جدول ضرب
در ریاضیات، جدول ضرب یک جدول ریاضی است که برای محاسبه عمل دوتایی ضرب استفاده میشود.
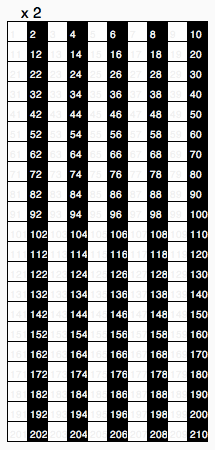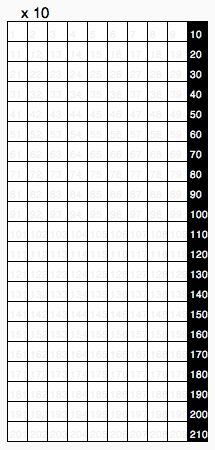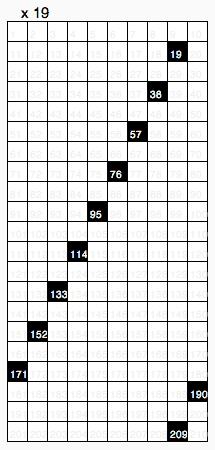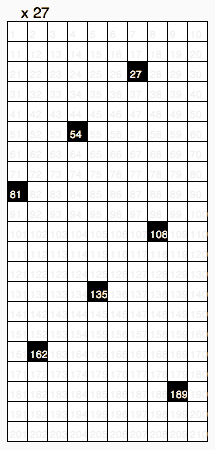
این جدول ضرب دهدهی بهطور سنتی به عنوان یک بخش ضروری از ریاضی ابتدایی در سراسر جهان تدریس میشود و آن را به عنوان شالودهای برای عملیات محاسباتی دهدهی میدانند.[۱]

تاریخچه
[ویرایش]قدیمیترین جدول ضرب شناخته شده توسط بابلیها در حدود ۴۰۰۰ سال پیش استفاده شدهاست ولی آنها از مبنای ۶۰ برای محاسبات استفاده میکردند.[۲][۲] قدیمیترین جدولی که با استفاده از یک پایه از مبنای ۱۰ شناخته شدهاست، جدول چینی است که در نوار بامبویی با قدمتی در حدود ۳۰۵ پیش از میلاد در چین مورد استفاده قرار میگرفتهاست.[۲]
جدول ضرب گاهی اوقات به ریاضیدان یونانی باستان فیثاغورس (۵۷۰–۴۹۵ پ. م) نسبت داده میشود اما بعضی نیز معتقد هستند مخترع اصلی چهار عمل اصلی ضرب،تقسیم،جمع،منها غیاث الدین جمشید کاشانی دانشمند بزرگ ایرانی هست که ماشین حسابهای امروزی مدیون او هستند... [۳][۴]
الگوها در جدول
[ویرایش]ضرب ۹ یک طرز نوشتن جالبی دارد که به صورت زیر است
۰=۱×۹
۱=۲×۹
۲=۳×۹
۳=۴×۹
۴=۵×۹
۵=۶×۹
۶=۷×۹
۷=۸×۹
۸=۹×۹
۹=۹×۱۰
ضرب هارا از عدد صفر شماره گذاری می کنیم تا آخر
سپس از پایین شماره گذاری می کنیم(از صفر)
۰۹=۱×۹
۱۸=۲×۹
۲۷=۳×۹
۳۶=۴×۹
۴۵=۵×۹
۵۴=۶×۹
۶۳=۷×۹
۷۲=۸×۹
۸۱=۹×۹
۹۰=۱۰×۹و جواب به دست میآید
یک الگو در جدول ضرب وجود دارد که میتواند به مردم برای حفظ آسانتر جدول کمک کند. این شکل از نوشتن جدول ضرب در ستون با تکمیل تعداد جملات است که هنوز هم مورد استفاده در برخی از کشورها است.
۱ × ۱۰ = ۱۰
۲ × ۱۰ = ۲۰
۳ × ۱۰ = ۳۰
۴ × ۱۰ = ۴۰
۵ × ۱۰ = ۵۰
۶ × ۱۰ = ۶۰
۷ × ۱۰ = ۷۰
۸ × ۱۰ = ۸۰
۹ × ۱۰ = ۹۰
| × | ۱ | ۲ | ۳ | ۴ | ۵ | ۶ | ۷ | ۸ | ۹ | ۱۰ | ۱۱ | ۱۲ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ۱ | ۱ | ۲ | ۳ | ۴ | ۵ | ۶ | ۷ | ۸ | ۹ | ۱۰ | ۱۱ | ۱۲ |
| ۲ | ۲ | ۴ | ۶ | ۸ | ۱۰ | ۱۲ | ۱۴ | ۱۶ | ۱۸ | ۲۰ | ۲۲ | ۲۴ |
| ۳ | ۳ | ۶ | ۹ | ۱۲ | ۱۵ | ۱۸ | ۲۱ | ۲۴ | ۲۷ | ۳۰ | ۳۳ | ۳۶ |
| ۴ | ۴ | ۸ | ۱۲ | ۱۶ | ۲۰ | ۲۴ | ۲۸ | ۳۲ | ۳۶ | ۴۰ | ۴۴ | ۴۸ |
| ۵ | ۵ | ۱۰ | ۱۵ | ۲۰ | ۲۵ | ۳۰ | ۳۵ | ۴۰ | ۴۵ | ۵۰ | ۵۵ | ۶۰ |
| ۶ | ۶ | ۱۲ | ۱۸ | ۲۴ | ۳۰ | ۳۶ | ۴۲ | ۴۸ | ۵۴ | ۶۰ | ۶۶ | ۷۲ |
| ۷ | ۷ | ۱۴ | ۲۱ | ۲۸ | ۳۵ | ۴۲ | ۴۹ | ۵۶ | ۶۳ | ۷۰ | ۷۷ | ۸۴ |
| ۸ | ۸ | ۱۶ | ۲۴ | ۳۲ | ۴۰ | ۴۸ | ۵۶ | ۶۴ | ۷۲ | ۸۰ | ۸۸ | ۹۶ |
| ۹ | ۹ | ۱۸ | ۲۷ | ۳۶ | ۴۵ | ۵۴ | ۶۳ | ۷۲ | ۸۱ | ۹۰ | ۹۹ | ۱۰۸ |
| ۱۰ | ۱۰ | ۲۰ | ۳۰ | ۴۰ | ۵۰ | ۶۰ | ۷۰ | ۸۰ | ۹۰ | ۱۰۰ | ۱۱۰ | ۱۲۰ |
| ۱۱ | ۱۱ | ۲۲ | ۳۳ | ۴۴ | ۵۵ | ۶۶ | ۷۷ | ۸۸ | ۹۹ | ۱۱۰ | ۱۲۱ | ۱۳۲ |
| ۱۲ | ۱۲ | ۲۴ | ۳۶ | ۴۸ | ۶۰ | ۷۲ | ۸۴ | ۹۶ | ۱۰۸ | ۱۲۰ | ۱۳۲ | ۱۴۴ |
با استفاده از این آمار و ارقام زیر میتوان جدول را آسانتر فرا گرفت:
| → | → | |||||||||
| ↑ | ۱ | ۲ | ۳ | ↓ | ↑ | ۲ | ۴ | ↓ | ||
|---|---|---|---|---|---|---|---|---|---|---|
| ۴ | ۵ | ۶ | ||||||||
| ۷ | ۸ | ۹ | ۶ | ۸ | ||||||
| ← | ← | |||||||||
| ۰ | ۵ | ۰ | ||||||||
| شکل ۱: فرد | شکل ۲: زوج | |||||||||
الگوهای ستونها، ردیفها و زنجیرهها
[ویرایش]جدول ضرب در مفهوم دارای ستونها، ردیفها و زنجیرههای بیشماری است. ستونها بهصورت عمودی و ردیفها بهصورت افقی در جدول قابل مشاهدهاند. زنجیرهها هم بهصورت اُریب در جدول مشاهده میشوند. در جدول ضرب بالا، ۱۲ ستون، ۱۲ ردیف و ۲۱ زنجیره دیده میشود. اجزای هر زنجیره، حلقه نام دارند و حداقل تعداد حلقههای یک زنجیره، ۲ حلقه است. ستونها، ردیفها بهصورت دوبهدو از الگویی ماندگار و ثابت پیروی میکنند و روند افزایشی آنها پیوسته یکسان است.
برای مثال، الگوی افزایش اعداد در ستون و ردیف یکم، عدد ۱ است و به ازای هر خانه، عدد ۱ به عدد پیشین افزوده میشود. این الگو در ستون و ردیف سوم، عدد ۳ است و به ازای هر خانه، ۳ عدد بهشمار پیشین افزوده میشود.[۵][۶]
روش پیدا کردن تعداد زنجیرههای یک جدول ضرب متقارن، به فرمول زیر است.
- تعداد زنجیرهها = ۳ - تعداد ردیفها + تعداد ستونها
متداول ترین روش های حفظ جدول ضرب
[ویرایش]- جدول ضرب مختصر : روشی بسیار مناسب که جدول ضرب را خلاصه می کند و راه بهتری برای حفظ کردن فراهم خواهد کرد.
- جدول ضرب با انگشتان دست : این روش کمک می کند که با چند نکته بتوان با استفاده از انگشت های دست ضرب را ساده تر آموخت.[۷]
- چرتکه : از جمله شاید جذاب ترین روش های ممکن برای کودکان باشد که می تواند بسیار کمک مهمی در این زمینه به کودکان بکند.[۸]
جستارهای وابسته
[ویرایش]منابع
[ویرایش]- ↑ Trivett, John (1980), "The Multiplication Table: To Be Memorized or Mastered?", For the Learning of Mathematics, 1 (1): 21–25, JSTOR 40247697.
- ↑ ۲٫۰ ۲٫۱ ۲٫۲ Jane Qiu (January 7, 2014). "Ancient times table hidden in Chinese bamboo strips". Nature News. doi:10.1038/nature.2014.14482.
- ↑ for example in "table+of+pythagoras"+-Montessori&source=bl&ots=TaXIEXCAic&sig=KiblQIMaPnnwRp-R0eW6CSEQUUk&hl=en&ei=IltFTezaDJH2sgatovGnDg&sa=X&oi=book_result&ct=result&resnum=3&ved=0CCcQ6AEwAg#v=onepage&q="table%20of%20pythagoras"%20-Montessori&f=false An Elementary Treatise on Arithmetic by John Farrar
- ↑ David E. Smith (1958), History of Mathematics, Volume I: General Survey of the History of Elementary Mathematics. New York: Dover Publications (a reprint of the 1951 publication), ISBN 0-486-20429-4, pp 58, 129.
- ↑ https://www.geeksforgeeks.org/matrix-chain-multiplication-dp-8/
- ↑ https://www.radford.edu/~nokie/classes/360/dp-matrix-parens.html
- ↑ «جدول ضرب | جدول ضرب کامل سوم ابتدایی - جدول ضرب». jdwalzarb.ir. بایگانیشده از اصلی در ۳ سپتامبر ۲۰۲۳. دریافتشده در ۲۰۲۳-۰۹-۰۳.
- ↑ الخزاعلة، عبير (۲۰۲۳-۰۹-۱۰). «جدول الضرب | تعليم جدول الضرب للاطفال من 1 الى 15». الرياضيات العربية (به عربی). دریافتشده در ۲۰۲۳-۰۹-۱۶.
- مشارکتکنندگان ویکیپدیا. «Multiplication table». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۱۰ نوامبر ۲۰۱۶.
