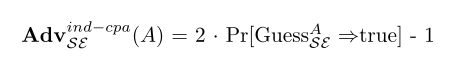تفکیک‌ناپذیری متن رمزنگاری‌شده

تفکیک‌ناپذیری متن رمزنگاری‌شده یک مشخصه در بسیاری از رویه‌های رمزنگاری است. به صورت شهودی، اگر یک سیستم رمزنگاری مشخصه‌ی تفکیک‌ناپذیری را داشته باشد، مهاجم نمی‌تواند بر اساس پیامی که رمزنگاری شده، جفت متن‌های رمزنگاری‌شده را از هم تمیز دهد. در بیشتر سیستم‌هایی که امنیت قابل اثباتی دارند و از رمزنگاری کلید عمومی استفاده می‌کنند، این مشخصه تحت حمله با متن اصلی منتخب یک پیش‌نیاز اساسی محسوب می‌شود، اگرچه برخی از رویه‌ها تحت حمله با متن رمز منتخب و حمله با متن رمز منتخب انطباقی نیز تفکیک‌ناپذیری ارائه می‌دهند. تفکیک‌ناپذیری تحت حمله با متن اصلی منتخب معادل خاصیت امنیت معنایی است، و بسیاری از اثبات‌هایی که در حوزه‌ی رمزنگاری هستند از این تعریف‌ها به صورت متقابل استفاده می‌کنند.

فرض کنید یک مهاجم، رمزنگاری یک پیام (که به صورت رندوم ازفضای پیام دو عنصری‌ای که خود مهاجم تعیین کرده انتخاب شده) را داشته باشد. اگر هیچ مهاجمی نتواند انتخاب پیام را با احتمالی که از احتمال رندوم ( ${\frac {1}{2}}$ ) بسیار بیشتر باشد تشخیص دهد، آن‌گاه سیستم رمزنگاری استفاده‌شده از لحاظ تفکیک‌پذیری امن است. اگر هر مهاجمی بتواند در تفکیک متن رمزشده‌ی منتخب با احتمالی بسیار بیشتر از رندوم ( ${\frac {1}{2}}$ ) موفق شود، آن‌گاه گفته می‌شود که مهاجم در زمینه‌ی تفکیک متن رمزنگاری‌شده یک «برتری» دارد، و همچنین رویه‌ی استفاده‌شده نیز از لحاظ تفکیک‌پذیری یک رویه‌ی امن محسوب نمی‌شود. همچنین این تعریف، این ایده را توضیح می‌دهد که در یک رویه‌ی امن، مهاجم نباید با دیدن متن رمزنگاری‌شده قادر باشد اطلاعاتی به دست بیاورد. بنابراین، مهاجم نباید بتواند با دقتی بهتر از رندوم عمل کند.

تعریف‌های رسمی

امنیت از لحاظ تفکیک‌پذیری، بسته به فرضیاتی که راجع به توانایی‌های مهاجم در نظر گرفته می‌شود، تعاریف بسیاری دارد. این امنیت معمولاً به عنوان یک بازی ارائه می‌شود. بازی به این صورت است که سیستم رمزنگاری امن محسوب می‌شود، اگر هیچ مهاجمی نتواند بازی را با احتمالی بسیار بیشتر از رندوم برنده شود. متداول‌ترین تعاریفی که در رمزنگاری استفاده می‌شوند عبارتند از تفکیک‌ناپذیری تحت حمله با متن اصلی منتخب (یا به صورت مخفف IND-CPA)، تفکیک‌ناپذیری تحت حمله‌ی غیرانطباقی با متن رمزنگاری‌شده‌ی منتخب (IND-CCA1) و تفکیک‌ناپذیری تحت حمله‌ی انطباقی با متن رمزنگاری‌شده‌ی منتخب (IND-CCA2). امنیت تحت هر کدام از این حملات، امنیت نسبت به حملات قبلی را نیز تضمین می‌کند: رویه‌ای که در IND-CCA1 امن است در IND-CPA نیز امن است. همچنین رویه‌ای که در IND-CCA2 امن است در IND=CCA1 و IND-CPA امن است. در نتیجه، IND-CCA2 در بین سه تعریف امنیت قوی‌ترین است.

تفکیک‌ناپذیری تحت حمله با متن اصلی منتخب (IND-CPA)

برای یک الگوریتم رمزنگاری نامتقارن احتمالاتی با کلید، تفکیک‌ناپذیری تحت حمله با متن اصلی منتخب (IND-CPA) با بازی ذیل بین یک مهاجم و یک «چالش‌گر» تعریف می‌شود. برای رویه‌هایی که بر پایه‌ی امنیت محاسباتی به وجود آمده‌اند، مهاجم به وسیله‌ی یک ماشین تورینگ با زمان چندجمله‌ای احتمالاتی مدل‌سازی می‌شود. این به این معنا است که مهاجم باید در زمانی چندجمله‌ای بازی را تمام کند و یک حدس ارائه بدهد. در این تعریف E(PK, M) نشان‌دهنده‌ی رمزنگاری یک پیام M با کلید PK است:

چالش‌گر بر اساس یک پارامتر امنیتی (به عنوان مثال تعداد بیت‌های کلید) یک جفت کلید PK, SK تولید می‌کند. PK را به مهاجم اعلام می‌کند و SK را پیش خودش نگه می‌دارد.
مهاجم می‌تواند تعدادی عملیات رمزنگاری یا عملیات از انواع دیگر را انجام دهد. مرتبه‌ی این عملیات باید چندجمله‌ای باشد.
در نهایت مهاجم دو متن اصلی مجزای $\scriptstyle M_{0},M_{1}$ را به چالش‌گر تحویل می‌دهد.
چالش‌گر یک بیت (b) را به صورت رندوم و با توزیع یک‌نواخت از بین صفر و یک انتخاب می‌کند. سپس متن رمزنگاری‌شده‌ی چالشی C = E(PK, $\scriptstyle M_{b}$ ) را به مهاجم اعلام می‌کند.
مهاجم آزاد است که به هر تعدادی که نیاز دارد محاسبه یا رمزنگاری انجام دهد. در انتها، مهاجم یک حدس برای مقدار b ارائه می‌دهد.

یک سیستم رمزنگاری را تفکیک‌ناپذیر تحت حمله با متن اصلی منتخب می‌گوییم، هرگاه همه‌ی مهاجم‌های با مرتبه‌ی زمانی چندجمله‌ای احتمالاتی تنها بتوانند مقدار ناچیزی از رندوم بهتر عمل کنند. زمانی می‌گوییم یک مهاجم مقدار ناچیزی از رندوم بهتر عمل کرده است که بازی را با احتمال $\scriptstyle \left({\frac {1}{2}}\right)\,+\,\epsilon (k)$ ببرد. $\scriptstyle \epsilon (k)$ یک تابع ناچیز در پارامتر امنیتی k است. این به این معنی است که برای همه‌ی تابع‌های چندجمله‌ای غیر صفر $\scriptstyle poly()$ یک $\scriptstyle k_{0}$ وجود دارد به صورتی که به ازای همه‌ی $\scriptstyle k\;>\;k_{0}$ بدانیم که $\scriptstyle |\epsilon (k)|\;<\;\left|{\frac {1}{poly(k)}}\right|$ .

اگرچه مهاجم $\scriptstyle M_{0}$ ، $\scriptstyle M_{1}$ و PK را می‌داند، ولی ذات احتمالاتی E به این معنی است که رمزنگاری $\scriptstyle M_{b}$ تنها یکی از همه‌ی متن‌های رمزنگاری‌شده‌ی معتبر خواهد بود. بنابراین رمزنگاری $\scriptstyle M_{0}$ و $\scriptstyle M_{1}$ و مقایسه‌ی نتایج رمزنگاری با متن رمزنگاری‌شده‌ی چالش به مهاجم برتری قابل توجهی نمی‌دهد.

با این که تعریف فوق تنها به یک سیستم رمزنگاری نامتقارن با کلید اختصاص داشد، ولی می‌توان آن را با حالت متقارن نیز منطبق کرد. این کار با جایگزینی تابع رمزنگاری کلید عمومی با ماشین اوراکل امکان‌پذیر است. ماشین اوراکل کلید خصوصی را پیش خود حفظ می‌کند، و هر متن دل‌خواهی که مهاجم انتخاب کند را رمزنگاری کرده و به او برمی‌گرداند.

بازی IND-CPA متقارن، تعریف رسمی

فرایند رقابتی انجام یک حمله با متن اصلی منتخب معمولاً در قالب یک بازی رمزنگاری تشریح می‌شود. برای ارزیابی IND-CPA متقارن، بازی‌ای که در بالا توضیح داده شد تعریف می‌شود.^[۱] فرض کنید ${\mathcal {K}}$ یک تابع تولید کلید، ${\mathcal {E}}$ یک تابع رمزنگاری و ${\mathcal {D}}$ یک تابع رمزگشایی باشد. فرض کنید ${\mathcal {S}}{\mathcal {E}}=({\mathcal {K}},{\mathcal {E}},{\mathcal {D}})$ یک رویه‌ی متقارن رمزنگاری است. بازی $Guess$ به صورت زیر تعریف می‌شود:

مهاجم به هر تعداد باری که بخواهد دو پیام بدون رمز را به انتخاب خودش در نظر می‌گیرد و آن‌ها را به LR Oracle می‌دهد. LR Oracle یک متن رمزنگاری‌شده برمی‌گرداند که در واقع رمزنگاری‌شده‌ی یکی از آن دو پیام است. «برتری» یک مهاجم با توجه به احتمال حدس زدن b به وسیله‌ی او ارزیابی می‌شود. b یک مقداری است که ابتدای فرایند به صورت رندوم انتخاب می‌شود، و مشخص می‌کند که چه پیامی به وسیله‌ی LR ORacle رمز می‌شود. بنابراین، «برتری» به صورت زیر تعریف می‌شود:^[۲]

تفکیک‌ناپذیری تحت حمله با متن رمز منتخب و حمله با متن رمز منتخب انطباقی (IND-CCA1 و IND-CCA2)

تفکیک‌ناپذیری تحت حمله با متن رمز منتخب و حمله با متن رمز منتخب انطباقی (IND-CCA1 و IND-CCA2) از تعریفی مشابه با تعریفی که در IND-CPA ارائه شد استفاده می‌کنند. در این حالت علاوه بر کلید عمومی (یا در رمزنگاری متقارن، اوراکل رمزنگاری)، مهاجم به اوراکل رمزگشایی نیز دسترسی دارد. کار این اوراکل این است که یک متن دل‌خواه رمزنگاری‌شده را تحویل می‌گیرد و متن اصلی را خروجی می‌دهد. در تعریف غیرانطباقی، مهاجم تا زمانی که متن رمزنگاری‌شده‌ی چالش را تحویل نگرفته می‌تواند از این اوراکل استفاده کند. در تعریف انطباقی، مهاجم می‌تواند به رمزگشایی متون دل‌خواه خود ادامه بدهد، حتی زمانی که متن رمزنگاری‌شده‌ی چالش را دریافت کرده است. البته شرطی وجود دارد، این که مهاجم نمی‌تواند عیناً متن رمزنگاری‌شده‌ی چالش را برای رمزگشایی به اوراکل بدهد. اگر بتواند این کار را انجام بدهد مسئله بسیار بدیهی خواهد شد.

چالش‌گر با در نظر گرفتن یک پارامتر امنیتی (به عنوان مثال تعداد بیت‌های کلید) یک جفت کلید PK, SK تولید می‌کند. سپس PK را به مهاجم اعلام می‌کند و SK را پیش خود نگه می‌دارد.
مهاجم می‌تواند هر تعداد باری که می‌خواهد عملیات رمزنگاری، عملیات رمزگشایی (با کمک اوراکل رمزگشایی و با هر متن دل‌خواه) و یا عملیات دیگری را انجام دهد.
در نهایت، مهاجم دو متن دل‌خواه و بدون رمز $\scriptstyle M_{0},\,M_{1}$ را انتخاب کرده و به چالش‌گر اعلام می‌کند.
چالش‌گر یک بیت را به صورت رندوم و با توزیع یک‌نواخت از بین صفر و یک انتخاب می‌کند. سپس متن رمزنگاری‌شده‌ی چالشی C = E(PK, $\scriptstyle M_{b}$ ) را به مهاجم اعلام می‌کند.
طرف مقابل آزاد است که هر تعداد محاسبه اضافی یا رمزگذاری را انجام دهد.
1. در حالت غیرانطباقی (IND-CCA1)، مهاجم دیگر نمی‌تواند از اوراکل رمزگشایی استفاده کند.
2. در حالت انطباقی (IND-CCA2) مهاجم باز هم می‌تواند از اوراکل رمزگشایی استفاده کند، با این شرط که نباید عیناً متن رمزنگاری‌شده‌ی چالش را رمزگشایی کند.
در نهایت، مهاجم حدس خود را برای مقدار b ارائه می‌دهد.

یک رویه زمانی نسبت به IND-CCA1/IND-CCA2 امن است که هیچ مهاجمی در برنده‌شدن بازی بالا نتواند نسبت به حالت تصادفی برتری قابل توجهی داشته باشد.

تفکیک‌ناپذیری نسبت به نویز تصادفی

گاهی اوقات ما به رویه‌های رمزنگاری‌ای احتیاج داریم که در آن‌ها رشته‌ی متن رمزنگاری‌شده از رشته‌ای که به صورت تصادفی به وسیله‌ی مهاجم تولید شده قابل تفکیک نباشد.^[۳]

اگر مهاجم قادر به تشخیص این که آیا یک پیام وجود دارد یا نه نباشد، آن‌گاه فردی که پیام را نوشته است انکاری محتمل و قابل قبول خواهد داشت.

بعضی از افرادی که لینک‌های ارتباطی رمزنگاری‌شده را می‌سازند ترجیح می‌دهند که کاری کنند که محتویات هر بسته‌ی اطلاعاتی که رد و بدل می‌شود از اطلاعات تصادفی قابل تفکیک نباشد. این کار باعث می‌شود که تجزیه و تحلیل ترافیک سخت‌تر شود.^[۴]

بعضی از افرادی که مسئول ساختن سیستم‌های مخصوص نگهداری اطلاعات رمزنگاری‌شده هستند، ترجیح می‌دهند که کاری کنند که اطلاعاتی که نگهداری می‌کنند از اطلاعات تصادفی قابل تفکیک نباشند. این کار باعث می‌شود که پنهان کردن اطلاعات ساده‌تر شود. به عنوان مثال برخی از برنامه‌هایی که روی دیسک‌ها عملیات رمزنگاری انجام می‌دهند (مثل TrueCrypt) تلاش می‌کنند که اطلاعات را در اطلاعات تصادفی‌ای پنهان کنند که ممکن است از پاک کردن اطلاعات قبلی به جا مانده باشند. به عنوان یک مثال دیگر، برخی از روش‌های پنهان‌نگاری تلاش می‌کنند کاری کنند که اطلاعاتی که می‌خواهند پنهان کنند با مشخصه‌های آماری نویز تصادفی عکس‌ها در عکس‌های دیجیتال مطابقت داشته باشد.

برای پشتیبانی از سیستم چنین رمزنگاری‌هایی که سیستم رمزنگاری قابل انکار نامیده می‌شوند، تعدادی الگوریتم رمزنگاری وجود دارد که به صورت مخصوص به این هدف طراحی شده‌اند که متن رمزنگاری‌شده از یک رشته‌ی تصادفی قابل تفکیک نباشد.^[۵]^[۶]^[۷]

بیشتر کاربردها به گونه‌ای هستند که به الگوریتمی که بتواند پیام رمزنگاری‌شده‌ای تولید کند که از یک رشته یا بیت‌های تصادفی قابل تشخیص نباشد، نیاز ندارند. با این حال، برخی نویسندگان اعتقاد دارند که چنین الگوریتم‌های رمزنگاری‌ای از لحاظ مفهومی از الگوریتم‌های دیگر ساده‌تر هستند، و کار کردن با آن‌ها نیز راحت‌تر است. علاوه بر این موارد، این الگوریتم‌ها در عمل نیز کاربردهای بیشتر و وسیع‌تری دارند. این طور که به نظر می‌آید بیشتر الگوریتم‌های رمزنگاری IND-CPA عملاً می‌توانند پیام رمزنگاری‌شده‌ای تولید کنند که از یک پیام با بیت‌های رندوم قابل تفکیک نباشند.^[۸]

هم‌ارزی‌ها و دلالت‌ها

تفکیک‌ناپذیر بودن، برای حفظ محرمانه بودن ارتباطات رمزنگاری‌شده مشخصه‌ی مهمی است. با این حال، مشخص شده است که در بعضی از حالت‌ها مشخصه‌ی تفکیک‌ناپذیر بودن بر مشخصه‌های امنیتی دیگری که به نظر بی‌ربط می‌آیند نیز اشاره می‌کند. در بعضی حالت‌ها این دلالت‌ها دوطرفه هستند. این به این معنی است که دو تعریف با هم هم‌ارز هستند؛ به عنوان مثال اثبات شده است که مشخصه‌ی تفکیک‌ناپذیری تحت حمله با متن رمز منتخب انطباقی (IND-CCA2)، با انعطاف‌ناپذیری تحت همین حمله (NM-CCA2) هم‌ارز است. این هم‌ارزی در نگاه اول بدیهی نیست، چون که انعطاف‌ناپذیری مشخصه‌ای است که با درستی و تمامیت پیام کار دارد، در حالی که تفکیک‌ناپذیری مربوط به محرمانه بودن است. در حالت‌های دیگر، اثبات شده است که تفکیک‌ناپذیری می‌تواند با برخی از تعاریف دیگر ترکیب شود تا دلالت بر تعریف‌های مفید دیگری داشته باشد، و برعکس. لیست ذیل شامل برخی از دلالت‌هایی است که تا به حال شناخته شده‌اند. این لیست به هیچ وجه کامل نیست.

علامت‌گذاری $\scriptstyle A\;\Rightarrow \;B$ نشان می‌دهد که مشخصه‌ی A بر مشخصه‌ی B دلالت دارد. $\scriptstyle A\;\Leftrightarrow \;B$ به این معنی است که مشخصه‌ی A و مشخصه‌ی B با هم هم‌ارز هستند. $\scriptstyle A\;\not \Rightarrow \;B$ یعنی مشخصه‌ی A لزوماً بر مشخصه‌ی B دلالت ندارد.

IND-CPA $\scriptstyle \Leftrightarrow$ امنیت معنایی تحت حمله با متن اصلی منتخب.
NM-CPA (انعطاف‌ناپذیری تحت حمله با متن اصلی منتخب) $\scriptstyle \Leftarrow$ IND-CPA.
NM-CPA (انعطاف‌ناپذیری تحت حمله با متن اصلی منتخب) $\scriptstyle \not \Leftarrow$ IND-CCA2.
NM-CCA2 (انعطاف‌ناپذیری تحت حمله با متن رمز منتخب انطباقی) $\scriptstyle \Leftrightarrow$ IND-CCA2.
حمله به قصد تفکیک
تفکیک‌ناپذیری محاسباتی
حمله با متن رمز منتخب
حمله با متن رمز منتخب انطباقی

منابع

↑ Bellare, Mihir; Rogaway, Phillip (May 11, 2005). "Introduction to Modern Cryptography, Chapter 5: Symmetric Encryption" (PDF). p. 93. Retrieved 6 April 2020.
↑ Bellare, Mihir; Rogaway, Phillip (May 11, 2005). "Introduction to Modern Cryptography, Chapter 5: Symmetric Encryption" (PDF). p. 93. Retrieved 6 April 2020.
↑ Chakraborty, Debrup; Rodríguez-Henríquez., Francisco (2008). Çetin Kaya Koç (ed.). Cryptographic Engineering. p. 340. ISBN 9780387718170.
↑ iang (2006-05-20). "Indistinguishable from random". Retrieved 2014-08-06.
↑ Bernstein, Daniel J.; Hamburg, Mike; Krasnova, Anna; Lange, Tanja (2013-08-28). "Elligator: Elliptic-curve points indistinguishable from uniform random strings" (PDF). Retrieved 2015-01-23.
↑ Möller, Bodo (2004). "A Public-Key Encryption Scheme with Pseudo-random Ciphertexts". Computer Security – ESORICS 2004. Lecture Notes in Computer Science. Vol. 3193. pp. 335–351. doi:10.1007/978-3-540-30108-0_21. ISBN 978-3-540-22987-2.
↑ Moore, Cristopher; Mertens, Stephan (2011). The Nature of Computation. ISBN 9780191620805.
↑ Rogaway, Phillip (2004-02-01). "Nonce-Based Symmetric Encryption" (PDF). pp. 5–6. Retrieved 2014-08-07.

Katz, Jonathan; Lindell, Yehuda (2007). Introduction to Modern Cryptography: Principles and Protocols. Chapman & Hall / CRC Press. ISBN 978-1584885511.

[:02-1] Bellare, Mihir; Rogaway, Phillip (May 11, 2005). "Introduction to Modern Cryptography, Chapter 5: Symmetric Encryption" (PDF). p. 93. Retrieved 6 April 2020.

[2] Bellare, Mihir; Rogaway, Phillip (May 11, 2005). "Introduction to Modern Cryptography, Chapter 5: Symmetric Encryption" (PDF). p. 93. Retrieved 6 April 2020.

[3] Chakraborty, Debrup; Rodríguez-Henríquez., Francisco (2008). Çetin Kaya Koç (ed.). Cryptographic Engineering. p. 340. ISBN 9780387718170.

[4] (2006-05-20). "Indistinguishable from random". Retrieved 2014-08-06.

[5] Bernstein, Daniel J.; Hamburg, Mike; Krasnova, Anna; Lange, Tanja (2013-08-28). "Elligator: Elliptic-curve points indistinguishable from uniform random strings" (PDF). Retrieved 2015-01-23.

[6] Möller, Bodo (2004). "A Public-Key Encryption Scheme with Pseudo-random Ciphertexts". Computer Security – ESORICS 2004. Lecture Notes in Computer Science. Vol. 3193. pp. 335–351. doi:10.1007/978-3-540-30108-0_21. ISBN 978-3-540-22987-2.

[7] Moore, Cristopher; Mertens, Stephan (2011). The Nature of Computation. ISBN 9780191620805.

[8] Rogaway, Phillip (2004-02-01). "Nonce-Based Symmetric Encryption" (PDF). pp. 5–6. Retrieved 2014-08-07.

[۱]

[۲]

[۳]

[۴]

[۵]

[۶]

[۷]

[۸]