انتخاب سریع

انتخاب سریع

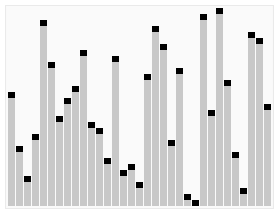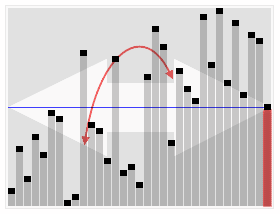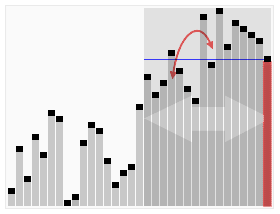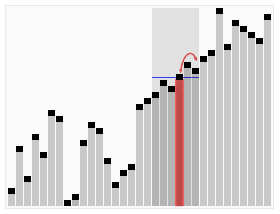کارکرد انتخاب سریع بر روی یک فهرست تصادفی از اعداد برای انتخاب 22امین کوچکترین عضو.
رده	الگوریتم انتخاب
ساختمان داده	آرایه
کارایی بدترین حالت	$O(n^{2})$
کارایی بهترین حالت	$O(n)$
کارایی متوسط	$O(n)$

در علوم رایانه، انتخاب سریع یک الگوریتم انتخاب برای پیدا کردن k امین عضو کوچک یک لیست است. همانند مرتب‌سازی سریع، این الگوریتم نیز توسط تونی هور توسعه داده شده و به همین دلیل به اسم الگوریتم انتخاب تونی هور نیز شناخته می‌شود. همانند مرتب‌سازی سریع، این الگوریتم نیز بهینه و دارای عملکرد حالت متوسط خوبی می‌باشد، اما عملکرد بدترین حالت ممکن این الگوریتم ضعیف است. انتخاب سریع و انواع دیگر آن از جمله الگوریتم‌های انتخابی هستند که در پیاده‌سازی‌های بهینه شده مورد استفاده قرار می‌گیرند.

انتخاب سریع از رویکرد یکسانی با مرتب‌سازی سریع بهره می‌برد، عضوی را به عنوان عنصر محوری انتخاب کرده و داده‌ها را بر پایهٔ آن به دو قسمت تقسیم می‌کند (دو قسمت کمتر و بیشتر از عنصر محوری). اگرچه به جای اینکه همانند مرتب‌سازی سریع بازگشت روی هر دو قسمت داده‌ها انجام شود، در انتخاب سریع بازگشت تنها روی یکی از این قسمت‌ها (قسمتی که دارای عضو k ام است) انجام می‌شود. به همین دلیل پیچیدگی این الگوریتم از $O(nlogn)$ به $O(n)$ کاهش می‌یابد.

همانند مرتب‌سازی سریع، انتخاب سریع نیز معمولاً به صورت الگوریتم درجا پیاده‌سازی می‌شود، و علاوه بر پیدا کردن k امین عضو، داده‌ها را نیز به صورت ناحیه‌ای مرتب می‌سازد. برای اطلاعات بیشتر دربارهٔ ارتباط انتخاب سریع با مرتب‌سازی به الگوریتم انتخاب رجوع کنید.

الگوریتم

در انتخاب سریع یک زیر رَویه به نام "تقسیم کننده" وجود دارد که می‌تواند یک لیست را به دو بخش (اعضای کوچکتر از یک عنصر خاص و اعضای بزرگتر از آن) تقسیم کند. شبه کد یک تقسیم‌کننده که یک تقسیم بر پایهٔ [list[pivotIndex انجام می‌دهد را در زیر می‌توانید مشاهده کنید:

 function partition(list, left, right, pivotIndex)
     pivotValue := list[pivotIndex]
     swap list[pivotIndex] and list[right]  // Move pivot to end
     storeIndex := left
     for i from left to right-1
         if list[i] < pivotValue
             swap list[storeIndex] and list[i]
             increment storeIndex
     swap list[right] and list[storeIndex]  // Move pivot to its final place
     return storeIndex

در مرتب‌سازی سریع با مرتب‌سازی هر قسمت به صورت بازگشتی به عملکردی در بهترین حالت با $O(nlogn)$ دست می‌یافتیم. در انتخاب سریع از قبل می‌دانیم که عضو مورد نظر ما در کدام یک از قسمت‌ها است و به همین دلیل تنها با یک بازگشت در هر مرحله می‌توانیم به عضو مورد نظر خود برسیم:

  // Returns the n-th smallest element of list within left..right inclusive
  // (i.e. left <= n <= right).
  // The search space within the array is changing for each round - but the list
  // is still the same size. Thus, n does not need to be updated with each round.
  function select(list, left, right, n)
     if left = right        // If the list contains only one element,
         return list[left]  // return that element
     pivotIndex  := ...     // select a pivotIndex between left and right,
                            // e.g., left + floor(rand() % (right - left + 1))
     pivotIndex  := partition(list, left, right, pivotIndex)
     // The pivot is in its final sorted position
     if n = pivotIndex
         return list[n]
     else if n < pivotIndex
         return select(list, left, pivotIndex - 1, n)
     else
         return select(list, pivotIndex + 1, right, n)

شباهت این الگوریتم به مرتب‌سازی سریع قابل توجه است: این الگوریتم علاوه بر یک انتخاب کننده، یک مرتب کنندهٔ جزئی نیز هست. در واقع این الگوریتم یک مرتب‌سازی سریع را به نحوی انجام می‌دهد که تنها $O(logn)$ از $O(n)$ قسمت داده‌ها مرتب می‌شوند. این رویهٔ ساده دارای عملکردی خطی است و همانند مرتب‌سازی سریع، در عمل نیز از عملکرد خوبی برخوردار است. از آنجایی که می‌توان از بازگشت دم بودن این الگوریتم با یک حلقه به صورت زیر صرف نظر کرد این الگوریتم یک الگوریتم درجا با سربار حافظهٔ ثابت است:

 function select(list, left, right, n)
     loop
         if left = right
             return list[left]
         pivotIndex := ...     // select pivotIndex between left and right
         pivotIndex := partition(list, left, right, pivotIndex)
         if n = pivotIndex
             return list[n]
         else if n < pivotIndex
             right := pivotIndex - 1
         else
             left := pivotIndex + 1

در صورتی که از پیاده‌سازی الگوریتم به صورت درجا صرف نظر کنیم تمامی توابع بالا را به صورت زیر می‌توان خلاصه کرد:

 QuickSelect(A, k)
   let r be chosen uniformly at random in the range 1 to length(A)
   let pivot = A[r]
   let A1, A2 be new arrays
   # split into a pile A1 of small elements and A2 of big elements
   for i = 1 to n
     if A[i] < pivot then
       append A[i] to A1
     else if A[i] > pivot then
       append A[i] to A2
     else
       # do nothing
   end for
   if k <= length(A1):
     # it's in the pile of small elements
     return QuickSelect(A1, k)
   else if k > length(A) - length(A2)
     # it's in the pile of big elements
     return QuickSelect(A2, k - (length(A) - length(A2))
   else
     # it's equal to the pivot
     return pivot

همانطور که در شبه کد مشاهده می‌کنید برای پیدا کردن k امین عضو کوچک، در هر مرحله لیست ما به دو لیست شامل اعضای بزرگتر و کوچکتر از pivot (عنصر محوری) تقسیم می‌شود (عنصر محوری به صورت تصادفی انتخاب می‌شود). در صورتی که طول لیست اول کوچکتر یا مساوی k باشد، یعنی k امین عنصر در لیست داده‌های کوچکتر از عنصر محوری قرار دارد و الگوریتم به صورت بازگشتی روی این ناحیه انجام می‌شود. در صورتی که k از طول لیست اولیه منهای طول لیست دوم بزرگتر باشد، k امین عضو در لیست دوم قرار دارد و در نتیجه بازگشت روی این بخش انجام می‌گیرد. اگر هیچ یک از شروط قبلی برقرار نباشند به این معناست که k امین عضو در واقع همان عنصر محوری انتخاب شده می‌باشد.

زمان اجرا

همانند مرتب‌سازی سریع، انتخاب سریع نیز دارای عملکرد حالت متوسط خوبی است، اما به شدت وابسته به عنصرهای محوری انتخاب شده می‌باشد. اگر عنصرهای محوری انتخاب شده مناسب باشند، به این معنا که تعداد داده‌ها را در هر مرحله با نسبت معینی کاهش دهند، تعداد داده‌ها به صورت نمایی کاهش می‌یابد و در نتیجه کارکرد الگوریتم به صورت خطی می‌شود. اگر عنصرهای محوری نامناسب به صورت پیاپی انتخاب شوند، مانند حالتی که در هر مرحله تنها یک عضو از داده‌ها کاسته شود، به بدترین عملکرد الگوریتم با $O(n^{2})$ منجر خواهد شد. برای مثال این اتفاق در حالتی رخ می‌دهد که برای پیدا کردن بزرگترین عضو در یک سری دادهٔ مرتب شده، عنصر محوری در هر مرحله اولین عضو از داده‌ها باشد. بدین ترتیب به سادگی می‌توان درستی رابطه‌ی زیر را برای بدترین زمان اجرا بررسی کرد:

$T(n)=\Theta (n)+T(n-1)=\Theta (n^{2})$

برای محاسبه‌ی زمان میانگین، با در نظر گرفتن تصادفی بودن عنصر محوری و فرض (غیر واقعی) اینکه بازگشت همواره در لیست بزرگتر اتفاق می‌افتد می‌توان نوشت:

$T(n)\leq \Theta (n)+{\frac {1}{n}}\sum _{i=1}^{n}T(\max(i,n-i-1))$

با در نظر گرفتن $T(n)\leq cn$ به عنوان فرض استقرا می‌توان نوشت:

$T(n)\leq a\cdot n+{\frac {1}{n}}\sum _{i=1}^{n}T(\max(i,n-i-1))$

$\Rightarrow T(n)\leq a\cdot n+{\frac {1}{n}}\sum _{i=1}^{\left\lfloor {\frac {n}{2}}\right\rfloor }T(n-i)+{\frac {1}{n}}\sum _{\left\lfloor {\frac {n}{2}}\right\rfloor +1}^{n}T(i)$

$\Rightarrow T(n)\leq a\cdot n+2\times {\frac {1}{n}}\sum _{\left\lfloor {\frac {n}{2}}\right\rfloor }^{n}T(i)$

$\Rightarrow T(n)\leq a\cdot n+2\times {\frac {1}{n}}\sum _{\left\lfloor {\frac {n}{2}}\right\rfloor }^{n}c\cdot i$

و حد بالای جمع سمت راست را به سادگی می‌توان بدست آورد:

$\sum _{\left\lfloor {\frac {n}{2}}\right\rfloor }^{n}i=\sum _{1}^{n}i-\sum _{1}^{\left\lfloor {\frac {n}{2}}\right\rfloor }i={\frac {n\cdot (n+1)}{2}}-{\frac {\left\lfloor {\frac {n}{2}}\right\rfloor \cdot (\left\lfloor {\frac {n}{2}}\right\rfloor +1)}{2}}\leq {\frac {n^{2}}{2}}-{\frac {\frac {n^{2}}{4}}{2}}={\frac {15}{32}}\cdot n^{2}$

چرا که $\left\lfloor {\frac {n}{2}}\right\rfloor$ همواره کوچکتر یا مساوی ${\frac {n}{2}}$ است. بنابراین:

$\Rightarrow T(n)\leq a\cdot n+{\frac {2\cdot c}{n}}\cdot {\frac {15}{32}}\cdot n^{2}=(a+{\frac {15}{16}}\cdot c)\cdot n$

در نتیجه به ازای $c>16a$:

$T(n)=O(n)$

از طرفی مشخص است که T(n) از Ω(n) نیز هست. بنابراین:

$T(n)=\Theta (n)$

انواع

انتخاب 6امین عدد کوچک یک لیست.

راحت‌ترین راه این است که عنصر محوری در هر مرحله به صورت تصادفی انتخاب شود، که قریب به یقین زمانی خطی را نتیجه می‌دهد. در استفادهٔ کاربردی معمولاً از روش میانهٔ سوم (مثلاً در مرتب‌سازی سریع) استفاده می‌شود که در صورتی که داده‌ها به صورت جزئی مرتب شده باشند به نتیجه‌ای خطی منجر خواهد شد. اگر چه این روش همچنان در دنباله‌های ساختگی ممکن است نتیجهٔ بدترین حالت ممکن را به دنبال داشته باشد؛ برای مثال دیوید ماسر یک سری کشندهٔ میانهٔ سوم (median-of-3 killer) را توصیف می‌کند که باعث شکست خوردن این روش می‌شود (این سری انگیزهٔ به وجود آمدن الگوریتم انتخاب درونگرا را در وی ایجاد کرد).

برای اطمینان پیدا کردن از عملکرد خطی حتی در بدترین حالت، می‌توان از الگوریتم پیچیده‌تری برای تعیین عنصر محوری استفاده کرد. برای این امر می‌توان از الگوریتم میانه‌ی میانه‌ها کمک گرفت. البته سربار محاسباتی تعیین عنصر محوری در این روش زیاد است و در عمل از این الگوریتم استفاده نمی‌شود؛ به همین دلیل می‌توان از انتخاب درونگرا استفاده کرد که با ترکیب انتخاب سریع با میانهٔ میانه‌ها، هم در حالت میانگین و هم در بدترین حالت، عملکردی خطی را نتیجه می‌دهد.

محاسبات دقیقتر برای پیچیدگی زمانی، برای عنصرهای محوری تصادفی نتیجه $n(2+2\log 2+o(1))\leq 3.4n+o(n)$ را می‌دهد (این نتیجه برای انتخاب میانه است، برای انتخاب سایر k‌ها نتیجه سریعتر است). این ثابت می‌تواند با استفاده از الگوریتم فلوید-ریوست تا ۳٫۲ بهبود یابد. این الگوریتم دارای عملکرد حالت میانگین $1.5n+O(n^{1/2})$ برای انتخاب میانه است (برای دیگر k‌ها سریعتر عمل می‌کند).