اتم ریدبرگ

شکل ۱: اوربیتال اتمی یک اتم ریدبرگ با n=۱۲. رنگ‌ها فاز کوانتومی الکترون به شدت برانگیخته شده را نشان می‌دهند.

شکل ۲: سطوح انرژی در اتم لیتیوم که سری ریدبرگ سه مقدار پایین مقدار حرکت زاویه‌ای مداری را نشان می‌دهد که به اولین انرژی یونش همگرا می‌شوند.

اتم ریدبرگ یک اتم برانگیخته است که یک یا چند الکترون آن دارای عدد کوانتومی اصلی بسیار بالا، n هستند. هرچه مقدار n بزرگتر باشد، الکترون به‌طور متوسط از هسته دورتر است. اتم‌های ریدبرگ دارای ویژگی‌های خاصی هستند، از جمله پاسخ بزرگ به میدان‌های الکتریکی و میدان‌های مغناطیسی، دوره‌های زوال طولانی و تابع موج الکترون که تحت شرایطی، به مدارهای کلاسیکی از الکترون‌ها در اطراف هسته‌ها شباهت دارند. الکترون‌های هسته‌ای الکترون بیرونی را از میدان الکتریکی هسته محافظت می‌کنند به طوری که از فاصله، پتانسیل الکتریکی مشابه با آنچه که در اتم هیدروژن تجربه می‌شود به نظر می‌رسد.

با وجود محدودیت‌هایش، مدل بور برای اتم در توضیح این ویژگی‌ها مفید است. کلاسیک، یک الکترون در یک مدار دایره‌ای با شعاع r، حول هسته هیدروژن با بار +e، از دومین قانون نیوتن پیروی می‌کند:

$\mathbf {F} =m\mathbf {a} \Rightarrow {ke^{2} \over r^{2}}={mv^{2} \over r}$

که در آن k = ۱/(۴πε₀).

حرکت مداری کوانتش شده است در واحدهای ħ:

$mvr=n\hbar$.

ترکیب این دو معادله منجر به عبارت بور برای شعاع مدار به‌طور واضح در مورد عدد کوانتومی اصلی، n می‌شود:

$r={n^{2}\hbar ^{2} \over ke^{2}m}.$

اکنون واضح است که چرا اتم‌های ریدبرگ ویژگی‌های خاصی دارند: شعاع مداری با مقیاس n² تغییر می‌کند (برای حالت n = 137 در هیدروژن، شعاع اتمی حدود ۱ میکرومتر است) و مقطع هندسی با مقیاس n⁴. بنابراین، اتم‌های ریدبرگ بسیار بزرگ هستند، با الکترون‌های ظرفیت به طور شل بسته شده که به راحتی توسط برخوردها یا میدان‌های خارجی مختل یا یونیزه می‌شوند.

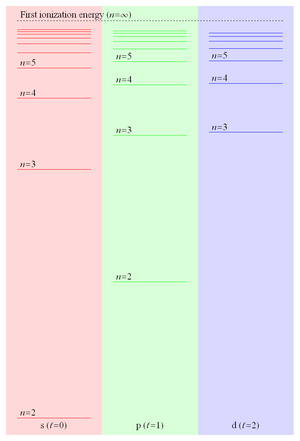
چون انرژی پیوند یک الکترون ریدبرگ متناسب با 1/r است و بنابراین مانند 1/n² کاهش می‌یابد، فاصله سطح انرژی مانند 1/n³ کاهش می‌یابد و منجر به سطوح بسیار نزدیک به هم می‌شود که به اولین انرژی یونش همگرا می‌شوند. این حالات ریدبرگ نزدیک به هم آن چیزی است که معمولاً به آن سری ریدبرگ گفته می‌شود. شکل ۲ برخی از سطوح انرژی پایین‌ترین سه مقدار عدد کوانتومی اوربیتالی در لیتیوم را نشان می‌دهد.

تاریخچه

وجود سری ریدبرگ برای اولین بار در سال ۱۸۸۵ زمانی که یوهان بالمر یک سری بالمر برای طول موجهای نور مرتبط با انتقالات در هیدروژن اتمی کشف کرد، به اثبات رسید. سه سال بعد، فیزیک‌دان سوئدی یوهانس ریدبرگ نسخه‌ای عمومی‌تر و شهودی‌تر از فرمول بالمر را ارائه داد که به فرمول ریدبرگ معروف شد. این فرمول وجود یک سری بی‌نهایت از تراز انرژیهای گسسته و به هم فشرده را نشان داد که به یک حد نهایی همگرا می‌شود.

این سری در سال ۱۹۱۳ به‌طور کیفی توسط نیلز بور با مدل مدل بور اتم هیدروژن توضیح داده شد که در آن کوانتش مقادیر حرکت زاویه‌ای منجر به سطوح انرژی گسسته مشاهده‌شده می‌شود. یک استنتاج کامل کمی از طیف مشاهده‌شده توسط ولفگانگ پاولی در سال ۱۹۲۶ پس از توسعه مکانیک کوانتومی توسط ورنر هایزنبرگ و دیگران به دست آمد.

جستارهای وابسته

• آشوب کوانتومی
• نظریه کوانتومی قدیمی