پیچ شیبدار

پیچ شیبدار پیچ یا تغییری در مسیر حرکت است که در آن وسیله نقلیه به سمت داخل پیچ متمایل یا شیب‌دار می‌شود. برای یک جاده یا خط‌آهن، این معمولاً به دلیل شیب عرضی جاده به سمت داخل منحنی است. زاویه شیب زاویه‌ای است که وسیله نقلیه نسبت به محور افقی، حول محور طولی خود، متمایل می‌شود.

پیچ روی سطوح مسطح

اگر زاویه شیب صفر باشد، سطح کاملاً مسطح بوده و نیروی نرمال به صورت عمودی رو به بالا است. تنها نیرویی که وسیله نقلیه را در مسیر خود نگه می‌دارد، اصطکاک یا کشش است. این نیرو باید به اندازه‌ای باشد که بتواند نیروی مرکزگرا را تأمین کند، رابطه‌ای که می‌تواند به صورت نامساوی زیر بیان شود، به‌فرض اینکه خودرو در دایره‌ای به شعاع $r$ حرکت کند:

$\mu mg>{mv^{2} \over r}.$

عبارت سمت راست شتاب مرکزگرا ضربدر جرم است، که نیروی مورد نیاز برای تغییر مسیر خودرو را نشان می‌دهد. عبارت سمت چپ، حداکثر نیروی اصطکاک است که برابر است با اصطکاک $\mu$ ضربدر نیروی نرمال. با بازآرایی، حداکثر سرعت پیچیدن به صورت زیر است:

$v<{\sqrt {r\mu g}}.$

توجه داشته باشید که $\mu$ می‌تواند ضریب اصطکاک ایستا یا اصطکاک جنبشی باشد. در حالت دوم، که خودرو در حال سر خوردن در پیچ است، اصطکاک به حداکثر مقدار خود می‌رسد و نامساوی‌ها به معادلات تبدیل می‌شوند. همچنین اثراتی مانند نیروی رو به پایین نادیده گرفته شده است، که می‌تواند نیروی نرمال و سرعت پیچیدن را افزایش دهد.

پیچ شیبدار بدون اصطکاک

بالا: توپی روی یک مسیر دایره‌ای شیبدار که با سرعت ثابت $v$ حرکت می‌کند؛ پایین: نیروهای وارد بر توپ. نیروی خالص وارد بر توپ، که با بردار اقلیدسی از نیروی نرمال اعمال‌شده توسط جاده و نیروی عمودی ناشی از گرانش به‌دست می‌آید، باید برابر با نیروی لازم برای شتاب مرکزگرا باشد که نیاز به حرکت در مسیر دایره‌ای را مشخص می‌کند.

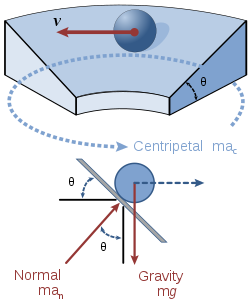
بر خلاف وسیله‌ای که در دایره‌ای مسطح حرکت می‌کند، لبه‌های شیبدار نیروی اضافی ایجاد می‌کنند که وسیله نقلیه را در مسیر خود نگه می‌دارد و مانع از «کشانده شدن به داخل» یا «رانده شدن به خارج» از دایره می‌شود (یا از حرکت جانبی چرخ راه‌آهن که تقریباً به فلنج چرخ مالیده شود جلوگیری می‌کند). این نیرو، مؤلفه افقی نیروی نرمال وسیله نقلیه (N) است. در نبود اصطکاک، نیروی نرمال تنها نیرویی است که در جهت مرکز دایره بر وسیله نقلیه اثر می‌گذارد؛ بنابراین، طبق قانون دوم نیوتن، می‌توانیم مؤلفه افقی نیروی نرمال را برابر با جرم ضربدر شتاب مرکزگرا قرار دهیم:

${mv^{2} \over r}=N\sin \theta$

از آنجا که در جهت عمودی حرکتی وجود ندارد، مجموع تمام نیروهای عمودی وارد بر سیستم باید صفر باشد؛ بنابراین، می‌توان مؤلفه عمودی نیروی نرمال وسیله نقلیه را برابر با وزن آن قرار داد:

$N\cos \theta =mg$

با حل معادله بالا برای نیروی نرمال و جای‌گذاری این مقدار در معادله قبلی، خواهیم داشت:

${mv^{2} \over r}={mg\tan \theta }$

این معادل است با:

${v^{2} \over r}={g\tan \theta }$

و با حل برای سرعت داریم:

$v={\sqrt {rg\tan \theta }}$

این سرعتی را ارائه می‌دهد که در نبود اصطکاک و با زاویه شیب مشخص و شعاع انحنا، اطمینان می‌دهد که وسیله نقلیه در مسیر تعیین‌شده خود باقی بماند. مقدار این سرعت همچنین به عنوان «سرعت نامی» (یا «سرعت تعادل» برای راه‌آهن) یک پیچ یا منحنی شناخته می‌شود. توجه داشته باشید که سرعت نامی منحنی برای همه اجسام سنگین یکسان است، و یک منحنی بدون شیب سرعت نامی برابر با صفر خواهد داشت.

پیچ شیبدار با اصطکاک

یک پیچ شیبدار تند در شیب‌راهی در شمال هیوارد، کالیفرنیا.

دوچرخه‌سواران در مسابقه‌ای در دانشگاه تافتس، یک پیچ تند و شیبدار به سمت پایین را طی می‌کنند.

هنگام بررسی اثرات اصطکاک در سیستم، لازم است دوباره به این نکته توجه کنیم که نیروی اصطکاک به کدام جهت اشاره دارد. هنگام محاسبه حداکثر سرعت برای خودرو، اصطکاک به سمت پایین شیب و به سمت مرکز دایره اشاره می‌کند؛ بنابراین، ما باید مؤلفه افقی اصطکاک را به نیروی نرمال اضافه کنیم. مجموع این دو نیرو، نیروی خالص جدید ما در جهت مرکز پیچ (نیروی مرکزگرا) خواهد بود:

$\underbrace {{mv^{2} \over r}=N\sin \theta } _{\text{Frictionless formula}}+\underbrace {\mu _{s}N\cos \theta } _{\text{Friction term}}$

دوباره، در جهت عمودی حرکتی وجود ندارد، که این امکان را می‌دهد تا همه نیروهای عمودی مخالف برابر در نظر گرفته شوند. این نیروها شامل مؤلفه عمودی نیروی نرمال که به سمت بالا اشاره می‌کند و وزن خودرو و مؤلفه عمودی اصطکاک که به سمت پایین اشاره می‌کنند، هستند:

$\underbrace {N\cos \theta =mg} _{\text{Frictionless formula}}+\underbrace {\mu _{s}N\sin \theta } _{\text{Friction term}}$

با حل معادله بالا برای جرم و جای‌گذاری این مقدار در معادله قبلی، خواهیم داشت:

${\frac {{\frac {N\cos \theta -\mu _{s}N\sin \theta }{g}}v^{2}}{r}}=N\sin \theta +\mu _{s}N\cos \theta$

با حل برای $v$ داریم:

$v_{\mathrm {max} }={\sqrt {rg\left(\sin \theta +\mu _{s}\cos \theta \right) \over \cos \theta -\mu _{s}\sin \theta }}={\sqrt {rg{\frac {\tan \theta +\mu _{s}}{1-\mu _{s}\tan \theta }}}}={\sqrt {rg\tan(\theta +\theta _{\mathrm {crit} })}}$

که در آن $\theta _{\mathrm {crit} }$ زاویه بحرانی است، به‌طوری که $\tan \theta _{\mathrm {crit} }=\mu _{s}$. این معادله حداکثر سرعت خودرو را با زاویه شیب، اصطکاک و شعاع انحنای مشخص ارائه می‌دهد. با تحلیل مشابه برای حداقل سرعت، معادله زیر به‌دست می‌آید:

$v_{\mathrm {min} }={\sqrt {rg\left(\sin \theta -\mu _{s}\cos \theta \right) \over \cos \theta +\mu _{s}\sin \theta }}={\sqrt {rg{\frac {\tan \theta -\mu _{s}}{1+\mu _{s}\tan \theta }}}}={\sqrt {rg\tan(\theta -\theta _{\mathrm {crit} })}}$

توجه کنید:

${\frac {v_{\mathrm {min} }}{v_{\mathrm {max} }}}={\sqrt {\frac {\tan(\theta -\theta _{\mathrm {crit} })}{\tan(\theta +\theta _{\mathrm {crit} })}}}$

تفاوت در تحلیل اخیر زمانی ایجاد می‌شود که جهت اصطکاک برای حداقل سرعت خودرو (به سمت بیرون دایره) در نظر گرفته شود. در نتیجه، عملیات‌های متضاد هنگام وارد کردن اصطکاک به معادلات نیروها در جهت مرکزگرا و عمودی انجام می‌شود.

منحنی‌های جاده‌ای با پهلوگردی نامناسب، خطر خروج از جاده و برخوردهای رو در رو را افزایش می‌دهند. کمبود ۲٪ در شیب عرضی (مثلاً ۴٪ شیب عرضی در یک منحنی که باید ۶٪ باشد) می‌تواند بسامد تصادفات را تا ۶٪ افزایش دهد، و کمبود ۵٪ این مقدار را تا ۱۵٪ افزایش می‌دهد. تاکنون، مهندسان جاده ابزارهای کارآمدی برای شناسایی منحنی‌های نامناسب و طراحی اقدامات اصلاحی مرتبط نداشته‌اند. یک پروفیلوگراف مدرن می‌تواند داده‌های مربوط به انحنای جاده و شیب عرضی (زاویه شیب) را فراهم کند. یک نمونه عملی برای ارزیابی پیچ‌های نامناسب در پروژه EU Roadex III توسعه داده شده است. به سند مرجع پیوند داده‌شده در زیر مراجعه کنید.

پهلوگردی در هوافضا

داگلاس دی‌سی-۳ در حال پهلوگردی برای انجام یک چرخش به چپ.

هنگامی که یک هواگرد ثابت‌بال در حال چرخش (تغییر مسیر) است، باید به موقعیت پهلوگردی متمایل شود تا بالهای آن به سمت جهت مورد نظر چرخش زاویه بگیرند. پس از اتمام چرخش، هواپیما باید به موقعیت بال‌های تراز برگردد تا پرواز مستقیم را از سر بگیرد.

هنگامی که هر وسیله نقلیه متحرک در حال چرخش است، لازم است که نیروهای وارد بر آن به نیروی خالص داخلی منجر شوند تا شتاب ایجاد شود. در مورد یک هواگرد در حال چرخش، نیرویی که باعث شتاب مرکزگرا می‌شود، مؤلفه افقی نیروی برآر وارد بر هواپیما است.

در پرواز مستقیم و سطح، نیروی برآر وارد بر هواپیما به صورت عمودی به سمت بالا عمل می‌کند تا وزن هواپیما که به سمت پایین وارد می‌شود را خنثی کند. اگر هواپیما بخواهد در پرواز سطحی باقی بماند (یعنی در فرازای ثابت)، مؤلفه عمودی باید همچنان برابر با وزن هواپیما باشد و بنابراین خلبان باید دسته کنترل را به عقب بکشد تا سکان افقی را برای دینامیک پرواز به سمت بالا هدایت کند و به این ترتیب زاویه حمله را افزایش دهد و برآر بیشتری ایجاد کند. نیروی برآر کل (اکنون زاویه‌دار) بیشتر از وزن هواپیما است. نیروی برآر اضافی همان مؤلفه افقی نیروی برآر کل است که نیروی خالصی ایجاد می‌کند و باعث شتاب داخلی هواپیما و اجرای چرخش می‌شود.

نمودار برداری که نیروی برآر و وزن وارد بر یک هواگرد ثابت‌بال در حین پیچ پهلوگردی را نشان می‌دهد. نیروی زرد نشان‌داده‌شده نمایانگر نیروی خالص است که باعث شتاب مرکزگرا می‌شود.

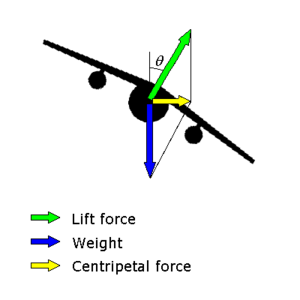
از آنجا که شتاب مرکزگرا به صورت زیر است:

$a={v^{2} \over r}$

در طول یک چرخش متعادل که زاویه پهلوگردی $\theta$ است، نیروی برآر در زاویه $\theta$ نسبت به عمودی عمل می‌کند. مفید است که نیروی برآر را به مؤلفه عمودی و مؤلفه افقی تفکیک کنیم.

قانون دوم نیوتن در جهت افقی به صورت زیر بیان می‌شود:

$L\sin \theta ={mv^{2} \over r}$

که در آن:

$L$ نیروی برآر وارد بر هواپیما است

$\theta$ زاویه پهلوگردی هواپیما است

$m$ جرم هواپیما است

$v$ سرعت حقیقی هواپیما است

$r$ شعاع چرخش است

در پرواز مستقیم و هم‌سطح، نیروی برآر برابر با وزن هواپیما است. در پرواز در حال چرخش، نیروی برآر از وزن هواپیما بیشتر می‌شود و برابر است با وزن هواپیما ($g$) تقسیم بر کسینوس زاویه پهلوگردی:

$L={mg \over {\cos \theta }}$

که در آن $g$ شدت میدان گرانشی است.

شعاع چرخش اکنون قابل محاسبه است:

$r={v^{2} \over {g\tan \theta }}$

این فرمول نشان می‌دهد که شعاع چرخش با مربع سرعت واقعی هوای هواپیما متناسب است. با افزایش سرعت هوا، شعاع چرخش بزرگ‌تر می‌شود و با کاهش سرعت هوا، شعاع کوچک‌تر می‌شود.

این فرمول همچنین نشان می‌دهد که شعاع چرخش با افزایش زاویه پهلوگردی کاهش می‌یابد. با افزایش زاویه پهلوگردی شعاع چرخش کوچک‌تر می‌شود و با کاهش آن شعاع بزرگ‌تر می‌شود.

در یک پیچ پهلوگردی در ارتفاع ثابت، ضریب بار برابر است با ${\frac {1}{\cos \theta }}$. می‌توان دید که ضریب بار در پرواز مستقیم و هم‌سطح برابر با $1$ است، زیرا $\cos(0)=1$، و برای تولید نیروی برآر کافی جهت حفظ ارتفاع ثابت، ضریب بار باید به بی‌نهایت نزدیک شود، زیرا زاویه پهلوگردی به $90^{\circ }$ نزدیک شده و $\cos \theta$ به $0$ نزدیک می‌شود. این از نظر فیزیکی غیرممکن است، زیرا محدودیت‌های ساختاری هواپیما یا توانایی فیزیکی سرنشینان پیش از این نقطه به پایان می‌رسند.

پیچ شیبدار در دو و میدانی

بیشتر مکان‌های دو و میدانی داخل سالن دارای پیچ‌های شیبدار هستند، زیرا پیست‌ها کوچک‌تر از پیست‌های فضای باز هستند. پیچ‌های تنگ در این پیست‌های کوچک معمولاً به شکلی طراحی شده‌اند که به ورزشکاران اجازه می‌دهد به سمت داخل خم شوند و نیروی گریز از مرکز را هنگام حرکت در منحنی خنثی کنند. این خم شدن به‌ویژه در دوهای سرعت قابل مشاهده است.

• 
  دونده‌های سرعت که در پیچ یک پیست داخل سالن به سمت داخل خم شده‌اند

جستارهای وابسته

• قوس شیب
• نیروی مرکزگرا
• نیروی گرانش

منابع

• مشارکت‌کنندگان ویکی‌پدیا. «Banked turn». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۴ ژانویه ۲۰۲۵.