مدار آرالسی

مدار RLC (به انگلیسی: RLC circuit) مدار الکتریکی شامل یک مقاومت، یک سلف و یک خازن است که به صورت موازی یا سری به هم متصل شدهاند. RLC متشکل از مقاومت، سلف و خازن است که نماد معمول برای مقاومت، سلف و خازن هستند. مدار RLC همانند مدار LC یک مدار نوسانساز است. وجود مقاومت، دامنه نوسانات مدار را در طول زمان به تدریج کاهش میدهد مگر آنکه آن را با یک منبع، ثابت نگاه داریم.[۱]
این مدار کاربردهای زیادی دارد. مثلاً در گیرندههای رادیویی و تلویزیون و مدارهای تشدیدگر به کار میرود. همچنین از این مدار میتوان به عنوان فیلتر بالاگذر یا فیلتر پایین گذر یا فیلتر میانگذر استفاده کرد. مدار RLC نوعی مدار درجه دوم است که برای تحلیل آن باید یک معادله دیفرانسیل درجه دو را حل کرد. این مدار را میتوان با توپولوژیهای مختلفی بست از جمله این که همه عناصر (قطعات) در آن سری باشند یا همه المانها موازی باشند که این دو حالت از سادهترین حالت هاست. در هریک از این حالات میتوان پاسخ طبیعی یا پاسخ پله مدار را تحلیل کرد.
مدار RLC سری
[ویرایش]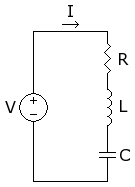
|
مدار RLC سری
|
|
همه عناصر (قطعات) میتوانند به صورت سری با منبع بسته شوند. برای تحلیل مدار در این حالت میتوان از قانون ولتاژ کیرشهف استفاده کرد.
که به ترتیب ولتاژهای مقاومت و سلف و خازن هستند و ولتاژ متغیر منبع در حوزه زمان است.
اگر نسبت به t مشتق گرفته و طرفین را بر L تقسیم کنیم داریم:
که با استفاده از نمادهایی که در مهندسی برق استفاده میشود میتوان آن را به این صورت نمایش داد:
در این رابطه فرکانس نپر یا ضریب تضعیف نامیده میشود که نشان میدهد که چه مدت بعد از این که منبع از مدار حذف شد، پاسخ گذرا در مدار موجود است. به فرکانس تشدید زاویهای میگویند. این دو مقدار برای مدار RLC سری عبارت است از:
- and
مدار Rlc موازی
[ویرایش] |
| مدارRLC موازی |
|
این مدار را میتوان با استفاده از رابطه دوگانی از مدار RLC سری بدست آورد بدین صورت که امپدانس الکتریکی هریک از المانها را مساوی با ادمیتانس عناصر (قطعات) متناظر در حالت سری در نظر گرفت. در این صورت کاملاً واضح است معادله دیفرانسیلی که از حل این مدار بدست میآید به صورت کلی همان معادله دیفرانسیل خواهد بود اما ضریب تضعیف آن به این صورت خواهد بود:
جستارهای وابسته
[ویرایش]منابع
[ویرایش]- ↑ مشارکتکنندگان ویکیپدیا. «RLC_circuit». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۳۰ اکتبر ۲۰۱۱.











