جابهجایی چرخشی
در ریاضیات ترکیبیاتی، جابهجایی چرخشی یا جابهجایی دَوَرانی یا شیفت دوری عملیاتی است که درایههای یک چندتایی را با حرکت دادن درایه انتهایی به موقعیت آغازین آن، مجدداً آرایش میدهد، در حالی که تمام درایههای دیگر به مکان بعدی خود نقل مکان میکنند، یا با عملی معکوس با آنچه توصیف شد، در جهت مخالف جابهجایی آرایهها صورت میپذیرد. جابهجایی دورانی نوع خاصی از جایگشت دوری است که به نوبه خود نوع خاصی از جایگشت است. بهطور صوری، جابهجایی دورانی را میتوان جایگشتی چون از n عنصر در نظر گرفت که در یک چندتایی قرار دارند چنانکه برای تمام به پیمانه n داریم:
یا:
برای نمونه، با اعمال جابهجایی دورانی بهطور مکرر روی چندتایی چهارتایی به صورت پشت سر هم به نتایج زیر میرسیم:
- (d, a, b, c),
- (c, d, a, b),
- (b, c, d, a),
- (a, b, c, d)
که تاپل آخر، همان تاپل اولیه ما میباشد.
مثال
[ویرایش]اگر دنباله بیتی تحت جابهجایی دورانی تکبیتی قرار بگیرد … (تصاویر زیر را ببینید):
 |
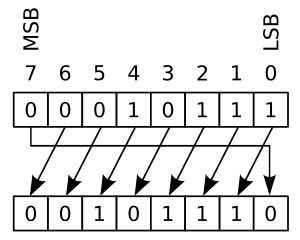 |
اگر دنباله بیتی تحت عملیات زیر قرار میگرفت:
| جابهجایی چرخشی راست با ۱ موقعیت: | ۰۱۰۰۱۰۱۱ |
| جابهجایی چرخشی راست با ۲ موقعیت: | ۱۰۱۰۰۱۰۱ |
| جابهجایی چرخشی راست با ۳ موقعیت: | ۱۱۰۱۰۰۱۰ |
| جابهجایی چرخشی راست با ۴ موقعیت: | ۰۱۱۰۱۰۰۱ |
| جابهجایی چرخشی راست با ۵ موقعیت: | ۱۰۱۱۰۱۰۰ |
| جابهجایی چرخشی راست با ۶ موقعیت: | ۰۱۰۱۱۰۱۰ |
| جابهجایی چرخشی راست با ۷ موقعیت: | ۰۰۱۰۱۱۰۱ |
| جابهجایی چرخشی راست با ۸ موقعیت: | ۱۰۰۱۰۱۱۰ |
| جابهجایی چرخشی چپ با ۱ موقعیت: | ۰۰۱۰۱۱۰۱ |
| جابهجایی چرخشی چپ با ۲ موقعیت: | ۰۱۰۱۱۰۱۰ |
| جابهجایی چرخشی چپ با ۳ موقعیت: | ۱۰۱۱۰۱۰۰ |
| جابهجایی چرخشی چپ با ۴ موقعیت: | ۰۱۱۰۱۰۰۱ |
| جابهجایی چرخشی چپ با ۵ موقعیت: | ۱۱۰۱۰۰۱۰ |
| جابهجایی چرخشی چپ با ۶ موقعیت: | ۱۰۱۰۰۱۰۱ |
| جابهجایی چرخشی چپ با ۷ موقعیت: | ۰۱۰۰۱۰۱۱ |
| جابهجایی چرخشی چپ با ۸ موقعیت: | ۱۰۰۱۰۱۱۰ |









