سطح پیچوار

سطحی پیچوار که منحنی نصف‌النهاری‌اش یک سهمی است.

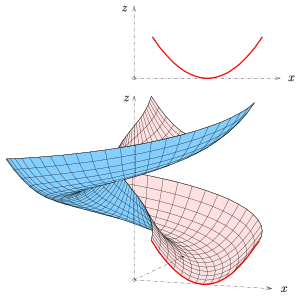
سطح پیچوار (انگلیسی: Helical Surfaces) حاصل حرکت پیچوار یک منحنی در فضای اقلیدسی است. در طول این حرکت هر نقطهٔ $p$ از منحنی مولد $c$ یک پیچوار $h_{p}$ را در فضا ترسیم می‌کند. بنابراین شبکه‌ای از منحنی‌های مولد $c$ و پیچوارهای مشابه سطح پیچوار را تشکیل می‌دهند. صفحهٔ مماس بر هر نقطهٔ $q$ روی این سطح با خطوط مماس $t_{c}$ و $t_{h}$ تعریف می‌شود که به‌ترتیب مماس بر منحنی مولد و مماس بر پیچوار هستند. منحنی تقاطع سطح پیچوار با صفحه‌ای که از محور پیچوار می‌گذرد منحنی نصف‌النهاری نام دارد.

برای مشخص‌کردن شکل سطح پیچوار غالباً از منحنی‌های نصف‌النهاری و مقاطع عرضی عمود بر محور پیچوار استفاده می‌شود. می‌توان نشان داد که سطح پیچوار را می‌توان با اعمال حرکت پیچوار به منحنی نصف‌النهاری یا مقطع عرضی تولید کرد و سطح نهایی در هر دو صورت یکی است.

توصیف ریاضی

اگر معادلهٔ پارامتری منحنی مولد $c(v)=(x(v),y(v),z(v))$ باشد، با اعمال حرکت پیچوار معادلهٔ پارامتری سطح پیچوار عبارت است از:

$x(u,v)=x(v)\cdot \cos {u}-y(v)\cdot \sin {u}$

$y(u,v)=x(v)\cdot \sin {u}+y(v)\cdot \cos {u}$

$z(u,v)=z(v)+p\cdot u$

با استفاده از منحنی نصف‌النهاری $m(v)=(x(v),0,z(v))$ در صفحهٔ $xz$ به عنوان منحنی مولد، این معادله به شکل زیر ساده‌سازی می‌شود:

$x(u,v)=x(v)\cdot \cos {u}$

$y(u,v)=x(v)\cdot \sin {u}$

$z(u,v)=z(v)+p\cdot u$

سطح پیچوار خاص

در مدلسازی‌ها غالباً از سطوح پیچداری استفاده می‌شود که منحنی مولد آن‌ها دایره یا خط مستقیم باشد. با استفاده از دایره به‌جای منحنی نصف‌النهاری یا مقطع عرضی، سطح تولیدشده سطحی کج لوله‌گونه حاصل می‌شود و با استفاده از دایره‌ای که صفحه‌اش بر مماس $t_{h}$ بر پیچوار عمود باشد حاصل لوله پیچوار خواهد بود.

حاصل اعمال حرکت پیچوار به خط مستقیم (یا پاره‌خط) سطح پیچوار خط‌دار خواهد بود. ساده‌ترین و مهمترین نوع آن پیچوارگونهٔ قائم است که منحنی مولدش خط مستقیم $g$ عمود در محور حرکت پیچوار است.

اگر پیچوار h و محور پیچوار A دو منحنی هادی سطح خط‌دار باشند، می‌توان دید که پیچوارگونهٔ قائم حالت خاصی از مخروط‌گون است. اگر منحنی مولد $g$ با نمایش پارامتری $c(v)=(v,0,0)$ نشان داده شود، معادله پارامتری پیچوارگون عبارت است از:

$x(u,v)=v\cdot cosu,$

$y(u,v)=v\cdot sinu,$

$z(u,v)=p\cdot u$

منابع

• مشارکت‌کنندگان ویکی‌پدیا. «Generalized helicoid». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۲۱ اوت ۲۰۲۰.
• Pottmann, Helmut; Asperl, Andreas; Hofer, Michael; Kilian, Axel; Bentley, Daril (2007). Architectural geometry. Bentley Institute Press. ISBN 1-934493-04-X. OCLC 180177477.